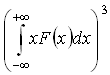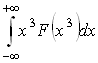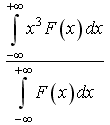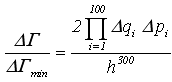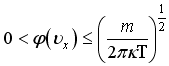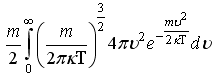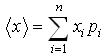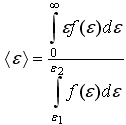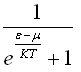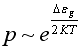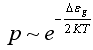- •2. Классическая статистика
- •2.1 Общее представление и элементы теории
- •Нт1(з). Если f(X) – плотность вероятности или функция распределения
- •3. Квантовая статистика. (72 задания).
- •4. Применение равновесных квантовых статистических распределений в физике твердого тела и газовых сред. (72 задания)
- •4.1. Общие представления и элементы теории.
- •4.2. Задачи
- •1 Эв неправ
- •3N колебательных мод с одинаковой фазовой скоростью
- •3N колебательных мод с фазовой скоростью неправ
- •3N колебательных мод с одинаковой фазовой скоростью
 НЕПРАВ
НЕПРАВ1 Эв неправ
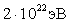
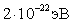
28)Если
число молекул идеального газа выросло
в четыре раза (N2=4N1),
а
![]() и
и
![]() ,
то относительное число молекул, имеющих
скорости от
,
то относительное число молекул, имеющих
скорости от
![]() до
до
![]() :
:
уменьшилось в 4 раза неправ
увеличилось в 2 раза
осталось прежним
увеличилось в 4 разаНЕПРАВ
29)Правильным
соотношением для функции распределения
молекул идеального газа по проекции
импульса
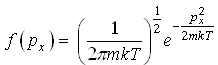 является:
является:
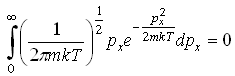
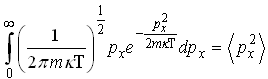
 неправ
неправ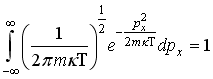
30)Для
функций распределения Максвелла по
проекциям импульсов
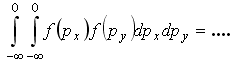
0-НЕПРАВ
31)Запишите
формулу для фазового объема, соответствующего
интервалу
и
объему V, используя шаблон
![]()
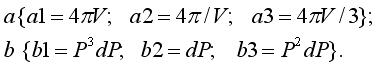
32)Запишите
формулу для распределения Бозе-Эйнштейна
по состояниям, используя шаблон
![]()
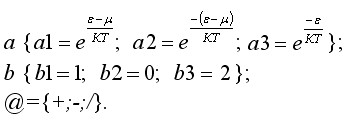
33)Если
![]() -
функции распределения по проекциям
скоростей для молекул идеального газа,
то:
-
функции распределения по проекциям
скоростей для молекул идеального газа,
то:

 НЕПРАВ
НЕПРАВ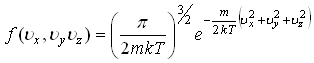
 НЕПРАВ
НЕПРАВ
34)Отношение теплоёмкости вырожденного электронного газа и теплоёмкости не вырожденного классического газа равно:
 НЕПРАВ
НЕПРАВ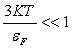
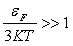
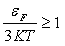 НЕПРАВ
НЕПРАВ
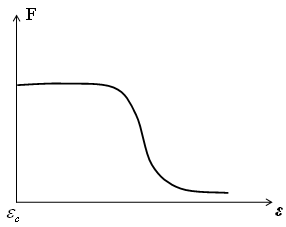
35)F(x)
– плотность вероятности или функция
распределения случайной величины х.
Среднее значение
![]() равно:
равно:
36)В модели Эйнштейна - Дебая постулируется, что N атомов кристалла должны иметь ...
бесконечное число колебательных мод с одинаковой скоростью
бесконечное число колебательных мод с фазовой скоростью
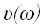
3N колебательных мод с одинаковой фазовой скоростью
3N колебательных мод с фазовой скоростью неправ
37)Если
F(x) – плотность вероятности или функция
распределения случайной величины х, то
выражение
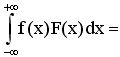
38)Зонный характер энергетического спектра электронов в кристаллах связан с . . .
вырождением состояний по магнитному квантовому числу
вырождением состояний по орбитальному квантовому числуНЕПРАВ
перекрытием волновых функций электронов из соседних атомов
рассеянием электронов на колебаниях атомов
39)Для данного газа в равновесном состоянии отношение средней энергии частиц к наиболее вероятной энергии при заданной температуре равно…
40)Среднее
время пролета валентного электрона в
поле действия ядра в кристалле
![]() Ширина
валентной зоны
Ширина
валентной зоны
![]() .
Постоянная Планка
.
Постоянная Планка
![]() .
Ответ округлить до десятых.
.
Ответ округлить до десятых.
41)Энергия
Ферми металла
эВ,
квазиимпульс электронов при этой энергии
![]() кг•м/c.
Масса свободного электрона
кг•м/c.
Масса свободного электрона
![]() кг,
эффективная масса электрона
кг,
эффективная масса электрона
![]() .
Отношение
.
Отношение
![]() равно
... Ответ округлить до целых.
равно
... Ответ округлить до целых.
42)Основной постулат статической физики утверждает, что микросостояния, принадлежащие одной …. , равновероятны
43)Для невырожденного полупроводника функция распределения электронов по энергиям в зоне проводимости имеет вид…
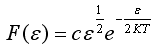
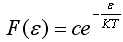

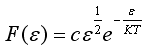
----------------------------------------------------------------------------------------------------------------------------------------------------
44)
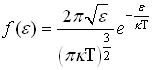 -
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Среднее значение
-
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Среднее значение
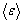 молекулы
идеального газа равно:
молекулы
идеального газа равно:
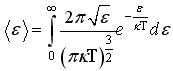
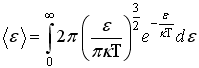
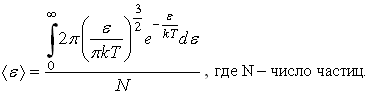 НЕПРАВ
НЕПРАВ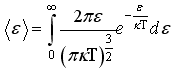
45)При T=const максимальное значение функции распределения по проекции импульса f(px):
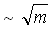
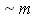
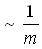
не зависит от

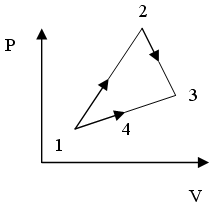
46)Изменение
энтропии
![]() и
и
![]() для
процессов, изображенных на P-T диаграмме:
для
процессов, изображенных на P-T диаграмме:
 НЕПРАВ
НЕПРАВ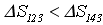
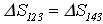
47)Энергия Ферми
![]() ,
средняя энергия фермионов при Т=0
,
средняя энергия фермионов при Т=0
![]() .
Отношение
.
Отношение
![]() ...
Округлить до десятых.
...
Округлить до десятых.
48)Плотность
вероятности или функция распределения
молекул идеального газа по проекции
скорости имеет вид
![]() ,
где нормированный множитель C равен:
,
где нормированный множитель C равен:
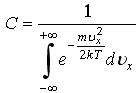
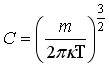
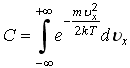 неправ
неправ
49)При Т=const максимальное
значение плотности вероятности
![]() с
увеличением массы молекул ……. Вставьте
слово.
с
увеличением массы молекул ……. Вставьте
слово.
Уменьшаеться-неправ
50)Для каждого типа частиц выберите их свойства:
|
антисимметричная волновая функция не подчиняются принципу Паули полуцелый спин целый спин подчиняются принципу Паули симметричная волновая функция |
Если
![]() –
функция распределения молекул идеального
газа по проекции скорости, то для
интегралов:
–
функция распределения молекул идеального
газа по проекции скорости, то для
интегралов:
 ,
,
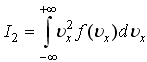 ,
,
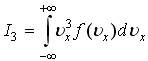 справедливо
следующее соотношение:
справедливо
следующее соотношение:
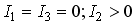
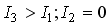

 неправ
неправ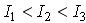

+ 1)Для циклического
процесса, изображенного на рис:
![]()
+ 2) Основной постулат квантовой статистики - это ...
принцип тождественности частиц
+ 3) Плотность квантовых состояний в энергетическом пространстве – это ...
число состояний в единичном малом интервале энергии
+ 4) F(x) – плотность
вероятности или функция распределения
случайной величины х. Среднее значение
![]() на
интервале от х1 до х2 равно:
на
интервале от х1 до х2 равно:

+ 5) Графики 1,2,3 соответствуют
трем функциям распределения Максвелла
по модулю импульса для одного и того же
газа в сосуде V при разных T. Наименьшей
энтропии соответствует график …..
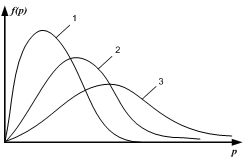 Ответ: 1
Ответ: 1
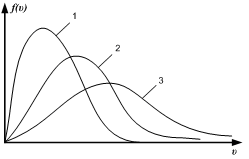
+ 6) На рисунке показано
распределение Максвелла по модулю
скорости для некоторого газа при разных
температурах. При этом площади под
кривыми (Si) и температуры (Тi)
удовлетворяют соотношению:
![]()
+ 7) Распределение электронов по состояниям в зоне проводимости невырожденного полупроводника приведено на рис. ...
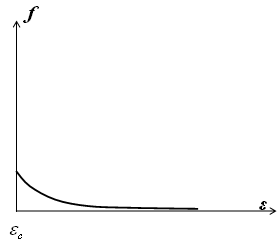
+ 8) Концентрация электронов в зоне проводимости собственного полупроводника возрастает с повышением Т за счёт перехода электронов
из валентной зоны в зону проводимости
+ 9) На рисунке приведено
распределение Бозе-Эйнштейна для двух
температур. Соотношение температур T2
… T1.
 Для
кривых выполняется соотношение:
Для
кривых выполняется соотношение:
![]()
+ 10) Если функция
распределения по энергии для молекул
идеального газа пронормирована на число
частиц
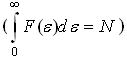 ,
то интеграл
,
то интеграл
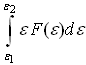 равен:
равен:
суммарной
энергии всех частиц, у которых
![]()
+ 11) Функция распределения
Ферми-Дирака по энергиям имеет вид...
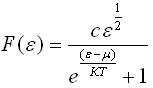
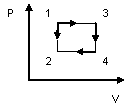
+ 12) Газ из состояния (1)
переходит в состояние (2) в одном случае
по прямой 1-2 , а в другом – по линии
1-3-4-2. При этом изменение энтропии:
![]()
+ 13) Вероятность Р наступления любого из двух независимых событий А или В равна:
сумме вероятностей Р(А)+Р(В)
+14) На рисунке приведено
распределение Ферми-Дирака по энергиям.
Площадь заштрихованной области
соответствует ...
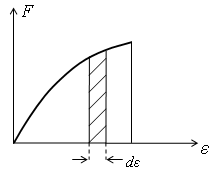
числу
частиц, энергия которых находится в
интервале
![]()
+ 15) Распределение электронов по энергиям в зоне проводимости невырожденного полупроводника приведено на рис. ...
+ 16) Функция распределения молекул
идеального газа по проекции скорости
![]() ,
пронормированная на 1, имеет вид:
,
пронормированная на 1, имеет вид:
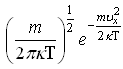
+ 17) Объем элементарной фазовой ячейки для одной квантовой частицы равен:
h3
+ 18) Функция распределения Ферми-Дирака по энергиям при Т=0 представлена на рисунке...
+ 19) Одному квантовому состоянию для N частиц (без учёта спина) соответствует фазовый объём …
h3N
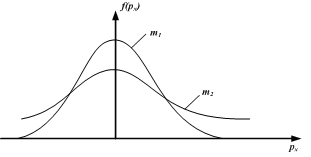
+ 20) Функции распределения молекул
идеального газа по проекции скорости
(плотность вероятности)
![]() для
разных газов, у которых m2>m1,
a T1=T2, показаны на рисунке:
для
разных газов, у которых m2>m1,
a T1=T2, показаны на рисунке:

+ 21) На рисунке приведено распределение
Ферми-Дирака.
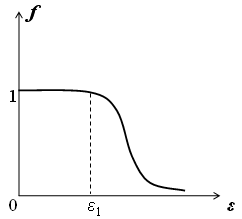 Состояния
с энергиями в интервале
Состояния
с энергиями в интервале
![]() заполнены
...
заполнены
...
полностью, в каждом находится один фермион
+ 22) Химический потенциал собственного полупроводника при Т=0 находится
в середине запрещенной зоны
+ 23) Функция распределения
 .
Это означает, что ...
.
Это означает, что ...
![]()
+ 24)
![]() -
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Заштрихованная площадь
равна:
-
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Заштрихованная площадь
равна:
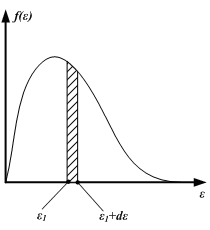
относительному
числу молекул
![]() ,
имеющих энергию от
,
имеющих энергию от
![]() до
до
![]()
+ 25) На рисунке изображена функция
распределения Ферми-Дирака по энергиям
при разных температурах.
 Кривая
1 соответствует Т1
Кривая 2
соответствует Т2
Кривая
1 соответствует Т1
Кривая 2
соответствует Т2
Т1=0; Т2>0
+ 26) Если
![]() -
плотность вероятности или функция
распределения случайной величины х ( х
изменяется от - ∞ до + ∞), то справедливо
любое выражение, кроме:
-
плотность вероятности или функция
распределения случайной величины х ( х
изменяется от - ∞ до + ∞), то справедливо
любое выражение, кроме:
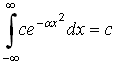
+ 27) Из приведенных величин: m –масса газа, S – энтропия, Т –температура, V –объем, Ω -статистический вес, n –концентрация частиц, p –давление - аддитивными являются:
m, S, V
+ 28) Для распределения Ферми-Дирака по
энергии выражение
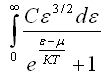 имеет
смысл …
имеет
смысл …
общая энергия всей системы фермионов
+29) Основной постулат квантовой статистики (принцип тождественности) является следствием того, что ...
описание движения отдельной частицы носит вероятностный характер
+ 30) Одному квантовому состоянию (без учёта спина) соответствует фазовый объём …
![]()
+ 31) Система фононов описывается статистикой
Бозе-Эйнштейна
+ 32) На рисунке приведено распределение
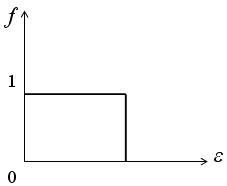
Ферми-Дирака
по состояниям при
![]()
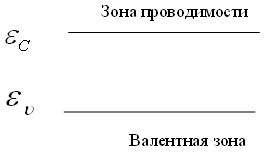
+ 31) Между свободной и валентной зонами
находится запрещённая зона шириной
![]() Валентная
зона при
Валентная
зона при
![]() заполнена
на половину. Кристалл является . . .
заполнена
на половину. Кристалл является . . .
проводником
+ 32) Принцип Паули утверждает, что ...
в одном квантовом состоянии может находиться не более одного фермиона
+ 33) При увеличении температуры основная причина роста электропроводности собственного полупроводника …
увеличение концентрации носителей тока
+ 34) Вероятность Р одновременного наблюдения 2-х независимых событий А и В равна:
произведению вероятностей Р(А)•Р(В)
+ 35) Одному квантовому состоянию для одной частицы в трехмерном пространстве соответствует фазовый объем
![]()
+ 36) Функция распределения Ферми-Дирака по модулю импульса при Т=0 представлена на рисунке …
+ 37) Среднее значение
![]() можно
найти, пользуясь любым выражением,
кроме…
можно
найти, пользуясь любым выражением,
кроме…
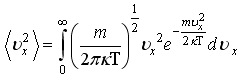
+ 38) Каждому типу полупроводника проводника выберите энергетическую диаграмму
|
· 2 · 1 · 3 |
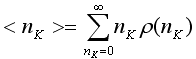 ,
где K – это …
,
где K – это …
набор квантовых чисел, задающих данное квантовое состояние свободного бозона
+ 40) Изменение энтропии
![]() при
плавлении льда (m-масса, λ -удельная
теплота плавления) равно:
при
плавлении льда (m-масса, λ -удельная
теплота плавления) равно:
![]()
+ 41) Статический вес системы:
зависит от числа частиц системы
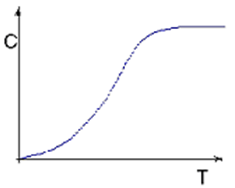
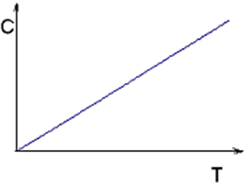
+42) Зависимость теплоёмкости твёрдого тела от температуры приведена на графикe …
+ 43) Функции распределения по проекции импульса рх (плотность вероятности) для разных газов, у которых m2>m1, а T1=T2, показаны на рисунке:
+ 44) Распределение Больцмана
![]() применимо
для ...
применимо
для ...
систем частиц малой плотности, у которых не проявляются квантовые свойства
+ 45) Распределение Максвелла по модулю скорости для некоторого идеального газа при Т1>Т2 показано на рисунке:

+ 46) Формула
![]() представляет
собой зависимость химического потенциала
от температуры для ...
представляет
собой зависимость химического потенциала
от температуры для ...
собственного полупроводника
+ 47) Функция распределения Ферми-Дирака по состояниям может быть получена, исходя из формулы:
,
где
вероятность
нахождения
![]() фермионов
в k -том квантовом состоянии
фермионов
в k -том квантовом состоянии
+ 48) При конденсации пара энтропия системы:
уменьшается
+ 49) На рисунке приведено распределение
Ферми-Дирака. Интервал энергий
![]() примерно
равен…
примерно
равен…
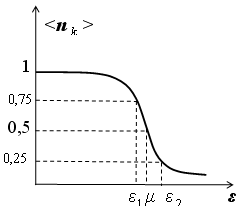
2KT
+ 50) Вероятность достоверного события равна ….Ответ: 1
+ 51) Реальные процессы в изолированных системах протекают:
в направлении увеличения хаотичности движения частиц в системе
+ 52) Для электронов в зоне проводимости невырожденного полупроводника следует применить распределение … Укажите все возможные варианты.
Максвелла
Ферми-Дирака
+53) Если F(x) – функция распределения
случайной величины х, а f(x2) –
некоторая функция этой величины, то

![]()
+ 54) Распределение Бозе-Эйнштейна по энергиям – это …
среднее число бозонов в единичном малом интервале энергии
+ 55) Если свойства системы частиц сильно зависят от квантовых свойств частиц, система является ...
определить нельзя
классической
вырожденной
невырожденной
+ 56) На рисунке приведено распределение
Ферми-Дирака.
 Каждое
состояние с энергией в интервале
заполнено
Каждое
состояние с энергией в интервале
заполнено
Частично
+ 57) Неправильным утверждением является. Вероятность случайного события Р:
Р изменяется от 0 до ∞
+ 58) Второе начало термодинамики утверждает, что в замкнутой системе:
ΔS≥0
+ 59) Теплоёмкость электронного газа в металлах …
![]() т.к.
средняя энергия теплового движения
электронов в металле
т.к.
средняя энергия теплового движения
электронов в металле
![]()
+ 60) Энергетический спектр электронов в кристаллах . . .
Или этот * состоит из разрешённых и запрещённых зон одинаковой ширины
* сплошной
* состоит из дискретных уровней, разделённых большими промежутками
Или этот * состоит из разрешённых и запрещённых зон одинаковой ширины
+ 61) Молекулы идеального газа :
могут иметь как целый, так и полу целый спин
+ 62) Условием нормировки функции распределения Максвелла по модулю скорости для молекул идеального газа является выражение:

+ 63) Изменение энтропии при изотермическом
квазиравновесном процессе 1-2:

ΔS12 = 0
+ 64) Функция распределения Ферми-Дирака
по состояниям находится по формуле
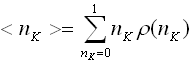 ,
где k – это ...
,
где k – это ...
Набор квантовых чисел, задающих квантовое состояние частицы в атоме
+ 65) Функция распределения частиц по энергиям в квантовой статистике определяется по формуле …
![]()
+66) В равновесной системе
![]()
0
+ 67) Для кристалла, состоящего из N атомов
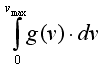 равен
равен
3N
+ 68) Функция распределения молекул идеального газа по модулю скорости (плотность вероятности) имеет размерность:
![]()
69)
+ 70) При равновесном тепловом излучении тело излучает и поглощает одно и то же количество энергии ...
за одно и то же время с одной и той же площади в одном и том же интервале частот dν
+71) Носителями тока в собственном полупроводнике являются …
электроны в зоне проводимости и дырки в валентной зоне
+ 72) Термодинамическая система находится в равновесном состоянии, если:
![]()
+ 73) Концентрация электронов собственного полупроводника зависит от температуры следующим образом …
![]()
+ 74) Энергия Ферми – это …
максимальная энергия фермионов при Т=0
+75) F(x) – плотность вероятности или функция распределения случайной величины х. Среднее значение равно:
76)
+ 77) Формула для концентрации электронов в зоне проводимости полупроводника n-типа имеет вид ...
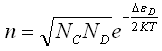
+ 78) При высоких температурах
![]() теплопроводность
твердого тела зависит от температуры
по закону ...
теплопроводность
твердого тела зависит от температуры
по закону ...
![]() ,
т.к. энергия колебаний ∼T,
а количество возбуждённых мод не меняется
нет
,
т.к. энергия колебаний ∼T,
а количество возбуждённых мод не меняется
нет
+ 79) Наиболее вероятное значение проекции
скорости
![]() для
молекул идеального газа равно:
для
молекул идеального газа равно:
0
80)
+ 81) Распределение Больцмана по состояниям имеет вид ...
![]()
+ 82)
![]() -
это
-
это
средняя квадратичная скорость, где m – масса одной молекулы
+ 83) Для получения полупроводника n-типа подбирают пятивалентную примесь, донорный уровень которой находится ...
в запрещённой зоне вблизи дна зоны проводимости
+ 84) Для получения полупроводника p-типа подбирают трехвалентную примесь, акцепторный уровень которой находится …
в запрещённой зоне вблизи потока валентной зоны
+ 85) Энергия квантового гармонического осциллятора равна
![]()
+ 86) Точка в фазовом пространстве для системы из N частиц характеризует:
положение в пространстве отдельной частицы
микросостояние системы
макросостояние системы
микросостояние отдельной частицы
87)
88)
89)
+ 90) Средние скорости молекул идеальных
газов, у которых
,
а массы молекул
![]()
![]()
+ 91) Длина волны де Бойля
![]() ,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
![]()
+ 92) В замкнутой системе энтропия может
меняться со временем, как показано на
участках:
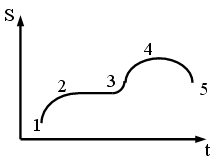
1-2-3
+ 93) Отношение электронной и решеточной теплоёмкостей для твёрдого тела при высоких температурах составляет …
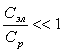
94)
+ 95) функция распределения Ферми-Дирака по модулю квазиимпульса равна …
![]()
96)
97)
98)
99)
+ 100)
![]() -
плотности вероятности или функции
распределения молекул по проекциям
скорости, для которых справедливо любое
соотношение, кроме…
-
плотности вероятности или функции
распределения молекул по проекциям
скорости, для которых справедливо любое
соотношение, кроме…
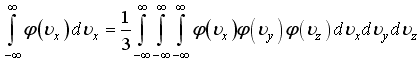
+ 101) Необходимым и достаточным условием равновесного состояния системы является:
стационарность макро- и микропараметров
замкнутость системы и стационарность микропараметров
замкнутость системы и стационарность макропараметров
стационарность макропараметров
+ 102) В одновалентных металлах валентная зона заполнена …
на две трети
наполовину
на одну треть
полностью
+ 103) Если
![]() -
плотность вероятности или функция
распределения молекул идеального газа
по энергии, то среднее значение
на
интервале энергий от
-
плотность вероятности или функция
распределения молекул идеального газа
по энергии, то среднее значение
на
интервале энергий от
![]() до
до
![]() равно:
равно:
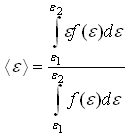
+ 104) Число возможных состояний системы
из N =100 квантовых частиц (электронов) в
конечном элементе объема
![]() равно:
равно:
1.В интервале
![]() число
квантовых состояний
число
квантовых состояний
![]() ,
число частиц
,
число частиц
![]() .
Для невырожденной системы выполняется
условие
.
Для невырожденной системы выполняется
условие
2. Плотность квантовых состояний в энергетическом пространстве – это ...
число состояний в единичном малом интервале энергии
3. Перейти от
классической функции распределения по
модулю скорости
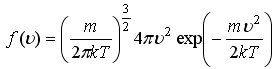 к
функции распределения по энергии f(e)
к
функции распределения по энергии f(e)
можно, заменив
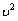 на
на
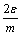 в
выражении
в
выражении
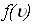
можно, заменив на и
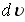 на
на
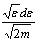 в
выражении
в
выражении
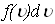
можно, заменив на и на
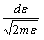 в
выражении
в
выражении
нельзя ни одним из этих преобразований
4. Функция распределения Бозе-Эйнштейна по состояниям имеет вид ...
5. Запишите формулу для среднего количества
фермионов в одном квантовом состоянии
при заданной энергии ε, используя шаблон

6. - это
средняя квадратичная скорость, где m – масса одной молекулы
7. Графики 1,2,3 соответствуют трем функциям распределения Максвелла по модулю импульса для одного и того же газа в сосуде V при разных T. Наименьшей энтропии соответствует график …..
8.
![]() если:
если:
V=const, T=const
нет правильного ответа
P=const, T=const
p=const, S=cons
9. Каждому типу полупроводника проводника выберите энергетическую диаграмму
|
|
10. При Т=0 химический потенциал собственного полупроводника μ= –0,5 эВ. Ширина запрещенной зоны рана … эВ.
11. В собственном полупроводнике проводимость обусловлена переходом электронов …
из валентной зоны в зону проводимости
12. - плотность вероятности или функция распределения молекул идеального газа по энергии. Среднее значение молекулы идеального газа равно:
13. Для равновесия двух подсистем замкнутой системы достаточно, чтобы у них были равны только:
14. В равновесном состоянии с ростом числа частиц N, относительная флуктуация δ ∼ Nm, где m=…
15. Для функций распределения Максвелла по проекциям импульсов 1/4
16. Формула для концентрации электронов в зоне проводимости полупроводника n-типа имеет вид ...
17. На рисунке приведено распределение Ферми-Дирака. Интервал энергий примерно равен…
2KT
18. Химический потенциал собственного полупроводника при Т=0 находится
в середине запрещенной зоны
19. При равновесном тепловом излучении тело излучает и поглощает одно и то же количество энергии ...
за одно и то же время с одной и той же площади в одном и том же интервале частот dν
20. Значения
интегралов
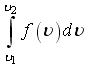 для
разных газов
для
разных газов
![]() при
одинаковых температурах:
при
одинаковых температурах:
нельзя сравнить, так как значения интеграла зависят от выбранного интервала скоростей
21. Функция распределения . Это означает, что ...
22. Функция распределения Ферми-Дирака по состояниям может быть получена, исходя из формулы:
, где вероятность нахождения фермионов в k -том квантовом состоянии
23. Изменение энтропии и для процессов, изображенных на P-T диаграмме:
24. -плотность вероятности или функция распределения молекул идеального газа по модулю скорости, для которой справедливо любое соотношение, кроме:
25. Распределение Больцмана по состояниям применимо при условии …
26. Если - функции распределения по проекциям скоростей для молекул идеального газа, то:
27. Распределение электронов по состояниям в зоне проводимости невырожденного полупроводника приведено на рис. ...
28. Для функции распределения Максвелла
по проекции импульса
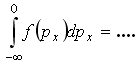
29. Если F(x) – плотность вероятности или функция распределения случайной величины х, то выражение f(x)
30. Если число молекул идеального газа выросло в четыре раза (N2=4N1), а и , то относительное число молекул, имеющих скорости от до :
осталось прежним
31. Распределение Бозе-Эйнштейна по состояниям – это ...
среднее количество бозонов в одном квантовом состоянии
32. При увеличении температуры идеального
газа Т2=4Т1 отношение
максимальных значений функций
распределения по проекции скорости

33. Энергия Ферми металла эВ. Эффективная масса электронов . Максимальная скорость электронов при Т=0 равна … км/с. Ответ округлить до сотен.
34. Формуле планка имеет смысл ...
Энергии фотонов, находящихся в единичном малом интервале частот
35. В одновалентных металлах валентная зона заполнена …
наполовину
36. Распределение Больцмана по состояниям имеет вид ...
37. Температура
вырождения системы
![]() .
Для невырожденной системы выполняется
условие ...
.
Для невырожденной системы выполняется
условие ...
38. Формула
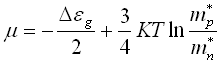 представляет
собой зависимость химического потенциала
от температуры для ...
представляет
собой зависимость химического потенциала
от температуры для ...
примесного полупроводника n–типа
40. Зависимость теплоёмкости твёрдого тела от температуры приведена на графикe …
41. Среднее количество электронов в
металле при T>0 в одном состоянии с
энергией
![]() равно
... Ответ записать в виде десятичной
дроби (округлить до десятых).
равно
... Ответ записать в виде десятичной
дроби (округлить до десятых).
42.
![]() -
соответственно: статистический вес,
энтропия, вероятность – связаны следующим
соотношением:
-
соответственно: статистический вес,
энтропия, вероятность – связаны следующим
соотношением:
43. Запишите формулу для количества квантовых состояний, соответствующих интервалу модуля скорости и объему V, используя шаблон
44. Необходимым и достаточным условием равновесного состояния системы является:
замкнутость системы и стационарность макропараметров
45. Число возможных состояний системы из N =100 квантовых частиц (электронов) в конечном элементе объема равно:
46. Химический потенциал фононов
![]()
47. Для молекул идеального газа значения интегралов и , где - наиболее вероятная энергия:
I1<I2
48. Между свободной и валентной зонами находится запрещённая зона шириной Валентная зона при заполнена на половину. Кристалл является . . .
проводником
49.На рисунке изображена функция распределения Ферми-Дирака по энергиям при разных температурах. Кривая 1 соответствует Т1 Кривая 2 соответствует Т2
Т1=0; Т2>0
50. Функция распределения Бозе-Эйнштейна по энергиям имеет вид ...
51. Найдите все возможные соответствия между левым и правым столбиками, если F(x) – плотность вероятности случайной величины х. Ответ дайте в виде: k-l, m-n, …
|
dP(x)/dx dP(x)dx < F(x) > dP(x) < x > 1 |
52. Изменение энтропии при плавлении льда (m-масса, λ -удельная теплота плавления) равно:
53. Функция распределения молекул идеального газа по проекции скорости , пронормированная на 1, имеет вид:
54. Концентрация электронов в зоне проводимости собственного полупроводника возрастает с повышением Т за счёт перехода электронов
из валентной зоны в зону проводимости
55. Точка в фазовом пространстве для системы из N частиц характеризует:
микросостояние системы
56. Одному квантовому состоянию (без учёта спина) соответствует фазовый объём …
57. Энергия Ферми – это …
максимальная энергия фермионов при Т=0
58. Распределение электронов по энергиям в зоне проводимости невырожденного полупроводника приведено на рис. ...
59. Если свойства системы частиц сильно зависят от квантовых свойств частиц, система является ...
вырожденной
60. Найдите неправильное утверждение. Фазовое пространство для N независимых частиц можно:
представить как 3N-мерный
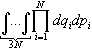 интеграл,
где qi={xi
yi
zi},
pi={pxi
pyi
pzi}
интеграл,
где qi={xi
yi
zi},
pi={pxi
pyi
pzi}
61. Перейти от
классической функции распределения по
модулю импульса
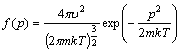 к
функции распределения по модулю скорости
f(u):
к
функции распределения по модулю скорости
f(u):
можно, заменив p на m
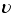 и dp на mdu в выражении f(p)dp
и dp на mdu в выражении f(p)dp
62. Функция распределения Ферми-Дирака по модулю квазиимпульса равна …
63. Функция распределения Бозе-Эйнштейна находится путём усреднения по формуле , где K – это …
набор квантовых чисел, задающих данное квантовое состояние свободного бозона
64. Из приведенных величин: m –масса газа, S – энтропия, Т –температура, V –объем, Ω -статистический вес, n –концентрация частиц, p –давление - аддитивными являются:
m, S, V
65. - плотность вероятности или функция распределения молекул идеального газа по энергии. Заштрихованная площадь равна:
относительному числу молекул , имеющих энергию от до
Если - плотность вероятности или функция распределения случайной величины х ( х изменяется от - ∞ до + ∞), то справедливо любое выражение, кроме:
66. Для
![]() -
плотности вероятности или функции
распределения Максвелла по модулю
скорости, справедливо выражение:
-
плотности вероятности или функции
распределения Максвелла по модулю
скорости, справедливо выражение:
67. Функция распределения молекул идеального газа по модулю скорости (плотность вероятности) имеет размерность:
68. Объем элементарной фазовой ячейки для одной квантовой частицы равен:
h3
69. Концентрация электронов собственного полупроводника зависит от температуры следующим образом …
70. Плотность квантовых состояний в энергетическом пространстве – это ...
число состояний в единичном малом интервале энергии
71. Для распределения
Ферми-Дирака по энергии выражение
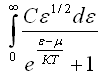 имеет
смысл …
имеет
смысл …
общая энергия всей системы фермионов
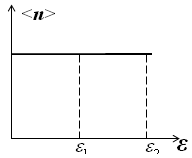
72. На рисунке представлены распределения
Ферми-Дирака по состояниям для двух
систем частиц;
![]() ,
,
![]() .
Отношение масс частиц
.
Отношение масс частиц
![]() =
...
=
...
73. Для невырожденной
системы среднее количество частиц в
одном квантовом состоянии
![]() равно
равно
74.Газ из состояния (1) переходит в состояние (2) в одном случае по прямой 1-2 , а в другом – по линии 1-3-4-2. При этом изменение энтропии:
75. На рисунке приведено распределение Ферми-Дирака по энергиям. Площадь заштрихованной области соответствует ...
числу частиц, энергия которых находится в интервале
76.
![]() если:
если:
S=const
p=const
T=const
77. Для кристалла, состоящего из N атомов равен
3N
78. В функции
распределения Максвелла по проекции
скорости

масса одной молекулы определенного газа
79. Плотность вероятности или функция распределения молекул идеального газа по проекции скорости имеет вид , где нормированный множитель C равен:
80. Правильным соотношением для функции распределения молекул идеального газа по проекции импульса является:
81. На рисунке приведено распределение Ферми-Дирака. Каждое состояние с энергией в интервале заполнено
Частично
Полностью
Наполовину
82.Энергетический спектр электронов в кристаллах . . .
состоит из разрешённых и запрещённых зон одинаковой ширины
состоит из разрешённых и запрещённых зон одинаковой ширины
Полностью
83. В равновесной системе
0
84. При высоких температурах теплопроводность твердого тела зависит от температуры по закону ...
, т.к. энергия колебаний ∼T, а количество возбуждённых мод не меняется
85. Для получения полупроводника p-типа подбирают трехвалентную примесь, акцепторный уровень которой находится …
в запрещённой зоне вблизи потока валентной зоны
86. Функция распределения Ферми-Дирака по энергиям имеет вид...
87. На рисунке
изображена функция распределения
Ферми-Дирака по модулю импульса при
разных температурах.
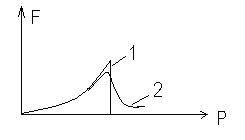 Кривая
1 соответствует Т1
Кривая 2 соответствует Т2
Кривая
1 соответствует Т1
Кривая 2 соответствует Т2
Т1=0; Т2>0
88.На рисунке показано распределение Максвелла по модулю скорости для некоторого газа при разных температурах. При этом площади под кривыми (Si) и температуры (Тi) удовлетворяют соотношению:
89. Основной постулат квантовой статистики - это ...
принцип тождественности частиц
90. Выражение
 имеет
смысл ...
имеет
смысл ...
энергии фотонного газа в единице объёма
91. Функция распределения Ферми-Дирака по состояниям – это …
среднее число фермионов в одном квантовом состоянии
92. Распределение фононов по состояниям имеет вид:
93. Для больших
частот
![]() спектральная
плотность энергии фотонного газа зависит
от частоты по закону ...
спектральная
плотность энергии фотонного газа зависит
от частоты по закону ...
![]()
94. Одному квантовому состоянию для N частиц (без учёта спина) соответствует фазовый объём …
h3N
95. Функция распределения частиц по энергиям в квантовой статистике определяется по формуле …
96. Концентрация дырок в валентной зоне полупроводника p-типа в области низких температур увеличивается за счёт перехода электронов …
из валентой зоны в зону проводимости
97. Второе начало термодинамики утверждает, что в замкнутой системе:
ΔS≥0
98. Функция распределения Ферми-Дирака по модулю импульса при Т=0 представлена на рисунке …
99. Термодинамическая система находится в равновесном состоянии, если:
100. Электроны, находящиеся в верхних разрешённых электрических зонах движутся . . .
хаотически по всему кристаллу в периодичном поле всех ядер
101. Реальные процессы в изолированных системах протекают:
в направлении увеличения хаотичности движения частиц в системе
102. Отношение электронной и решеточной теплоёмкостей для твёрдого тела при высоких температурах составляет …
103.
![]() -
плотность
вероятности или функция распределения
по проекции скорости для молекул
идеального газа принимает значения:
-
плотность
вероятности или функция распределения
по проекции скорости для молекул
идеального газа принимает значения:
104. Энтропия неизолированной системы при необратимом теплообмене:
только увеличивается
может как и увеличиваться, так и уменьшаться в зависимости от условий
только уменьшается
не изменяется
105. Среднее значение
![]() для
одноатомного идеального газа можно
рассчитать, пользуясь любым выражением,
кроме …
для
одноатомного идеального газа можно
рассчитать, пользуясь любым выражением,
кроме …
106. Изменение энтропии при переходе из состояния (1) в состояние (2):
нельзя определить, так как неизвестно соотношение температур
107. Если х - случайная
физическая величина, принимающая ряд
дискретных значений х1,
х2,
…хп,
а Рi
– вероятность появления xi,
то среднее значение
![]() равно:
равно:
108. Длина волны де Бойля , среднее расстояние между частицами l. Для невырожденной системы выполняется условие ...
109.Распределение
Максвелла-Больцмана для идеального
газа имеет вид:
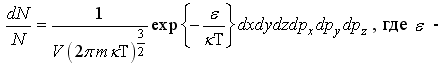
потенциальная энергия частиц во внешнем поле плюс суммарная кинетическая энергия молекул
110. Одному квантовому состоянию для одной частицы в трехмерном пространстве соответствует фазовый объем
111. Каноническое распределение Гиббса имеет вид , где постоянная С равна :
112. Если F(x) –
плотность вероятности или функция
распределения случайной величины х, то
выражение
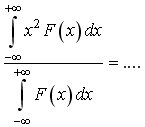
113. -плотности вероятности или функции распределения молекул по проекциям скорости, для которых справедливо любое соотношение, кроме…
114. Условием нормировки функции распределения Максвелла по модулю скорости для молекул идеального газа является выражение:
115. Концентрация электронов в зоне проводимости примесного проводника n-типа в области низких температур увеличивается за счёт перехода электронов …
с донорного уровня в зону проводимости
с донорного уровня в зону проводимости
116. -плотность вероятности или функция распределения случайной величины х, Нормированный множитель С равен:
117. Носителями тока в собственном полупроводнике являются …
электроны на донорных уровнях и дырки в валентной зоне
только дырки в валентной зоне
электроны в зоне проводимости и дырки в валентной зоне
118. При T=const максимальное значение функции распределения по проекции импульса f(px):
119. Основной постулат квантовой статистики (принцип тождественности) является следствием того, что ...
описание движения отдельной частицы носит вероятностный характер
120. Случайная
величина х принимает значения от 0 +∞.
Функция распределения случайной величины
х или плотность вероятности имеет вид
![]() ,
где нормировочный множитель С равен:
,
где нормировочный множитель С равен:
b
121. Зонный характер энергетического спектра электронов в кристаллах связан с . . .
перекрытием волновых функций электронов из соседних атомов
122.На рисунке приведено распределение Бозе-Эйнштейна для двух температур. Соотношение температур T2 … T1. Для кривых выполняется соотношение:
123.Ширина разрешенной энергетической зоны в одновалентном кристалле имеется N=1022 атомов. Расстояние между соседними подуровнями в зоне равно
124. Для классической
функции распределения по модулю скорости
при условии Т=const, а u2>u1
отношение
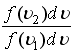
всегда >1
>1, если υ1<υнв<υ2
<1, если υ1 и υ2 меньшеυнв
>1, если υ1 и υ2 меньшеυнВ
<1, если υ1 и υ2 большеυнв
125. У изолированной системы, находящейся в равновесном состоянии:
E = Emin
Ω=Ωmin
126. f(x2)
– некоторая функция случайной величины
x. Интеграл
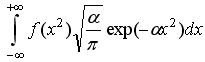 равен:
равен:
127. Если - плотность вероятности или функция распределения молекул идеального газа по энергии, то среднее значение на интервале энергий от до равно:
128. Функция распределения по энергии в квантовой статистике – это
плотность вероятности нахождения частицы в интервале

вероятность нахождения частицы с энергией

среднее число частиц с энергией
среднее число частиц в единичном малом интервале энергии
129. При стремлении изолированной системы к равновесному состоянию:
130. Функция распределения Ферми-Дирака по состояниям имеет вид …
131. Для N квантовых частиц объем минимальной фазовой ячейки, приходящейся на одно квантовое микросостояние системы, ΔГmin равен:
h3N
132. Для циклического процесса, изображенного на рис:
133. Длина волны де Бойля , среднее расстояние между частицами l. Для невырожденной системы выполняется условие ...
134. Для электронов в зоне проводимости невырожденного полупроводника следует применить распределение … Укажите все возможные варианты.
Максвелла
Ферми-Дирака
135. Функция распределения Ферми-Дирака по состояниям находится по формуле , где k – это ...
Набор квантовых чисел, задающих квантовое состояние частицы в атоме
136. В замкнутой системе энтропия может меняться со временем, как показано на участках:
2-3-4
4-5
1-2-3-4
1-2-3
137. Для электронного газа в металле имеет смысл
количества электронов в зоне проводимости
138. Теплоёмкость электронного газа в металлах …
т.к. средняя энергия теплового движения электронов в металле
139. Функция распределения Бозе-Эйнштейна по состояниям может быть получена путём усреднения по формуле ...
, где - то же, что и в пункте А
140. На рисунке приведены графики изохоры, изобары, изотермы, адиабаты. Правильные названия графиков:
1-адиабата, 2-изохора, 3-изобара, 4-изотерма
141. Если – функция распределения молекул идеального газа по проекции скорости, то для интегралов: , , справедливо следующее соотношение:
142. Для малых частот
![]() спектральная
плотность энергии фотонного газа зависит
от частоты по закону . . .
спектральная
плотность энергии фотонного газа зависит
от частоты по закону . . .
143. Энергия квантового гармонического осциллятора равна
144. Средние скорости молекул идеальных газов, у которых , а массы молекул
145. Система фононов описывается статистикой
Бозе-Эйнштейна
146. Выражение
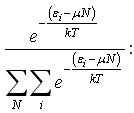
равно вероятности встретить подсистему, состоящую из N частиц, в состоянии с энергией εi
147. Функция распределения Ферми-Дирака по энергиям при Т=0 представлена на рисунке...
148. Число доступных
состояний в элементе фазового пространства
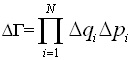 для
классической частицы:
для
классической частицы:
→ ∞
149. Концентрация дырок в валентной зоне собственного полупроводника зависит от температуры следующим образом:
150. При низких
температурах
![]() теплоёмкость
твёрдого тела зависит от температуры
по закону
теплоёмкость
твёрдого тела зависит от температуры
по закону
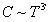 ,
т.к. новые моды упругих колебаний
оказываются возбуждёнными
,
т.к. новые моды упругих колебаний
оказываются возбуждёнными
151. Число доступных микросостояний в некотором фазовом объеме ΔГ:
одинаково для классической и квантовой частицы
конечно для классической частицы, т.к. она имеет определенные размеры
бесконечно для квантовой частицы, т.к. ее размерами можно пренебречь
бесконечно для классической частицы, т.к. в каждый момент времени объем, который в фазовом пространстве определяет ее состояние, стремится к нулю
152. В модели Эйнштейна - Дебая постулируется, что N атомов кристалла должны иметь ...