
- •2. Классическая статистика
- •2.1 Общее представление и элементы теории
- •Нт1(з). Если f(X) – плотность вероятности или функция распределения
- •3. Квантовая статистика. (72 задания).
- •4. Применение равновесных квантовых статистических распределений в физике твердого тела и газовых сред. (72 задания)
- •4.1. Общие представления и элементы теории.
- •4.2. Задачи
- •1 Эв неправ
- •3N колебательных мод с одинаковой фазовой скоростью
- •3N колебательных мод с фазовой скоростью неправ
- •3N колебательных мод с одинаковой фазовой скоростью
2. Классическая статистика
2.1 Общее представление и элементы теории
НТ1(З). Каноническое распределение Гиббса имеет вид
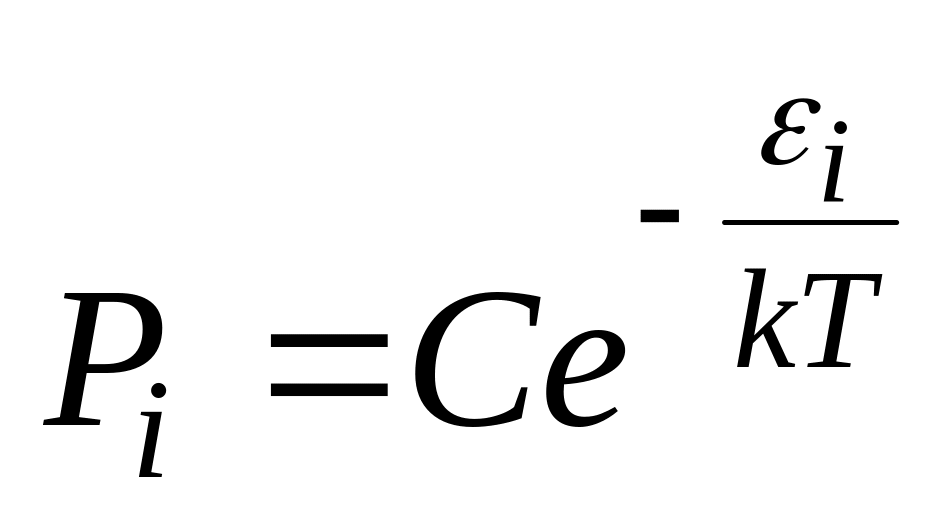 ,
где постоянная
,
где постоянная
С
равна :
![]()
А)
![]() ;
;
В)
![]() ;
;
*С)
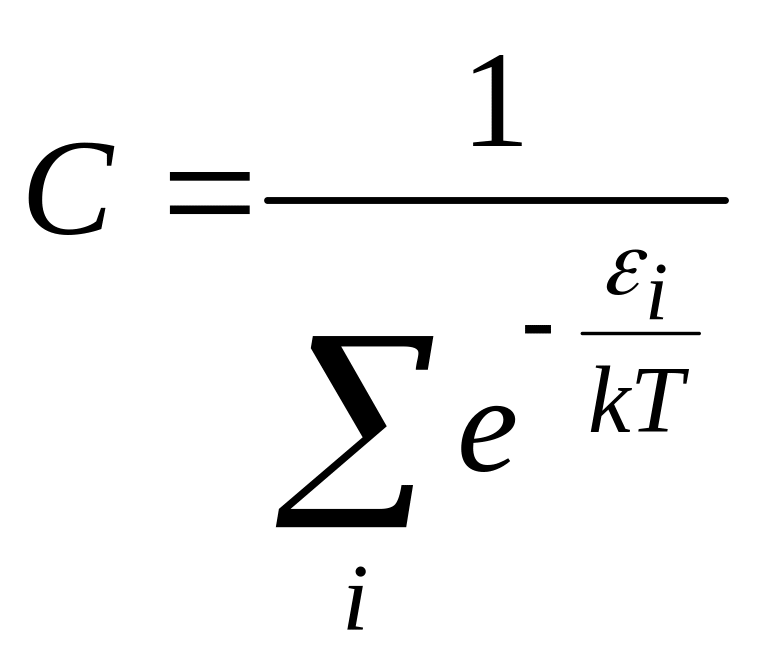 ;
;
D)
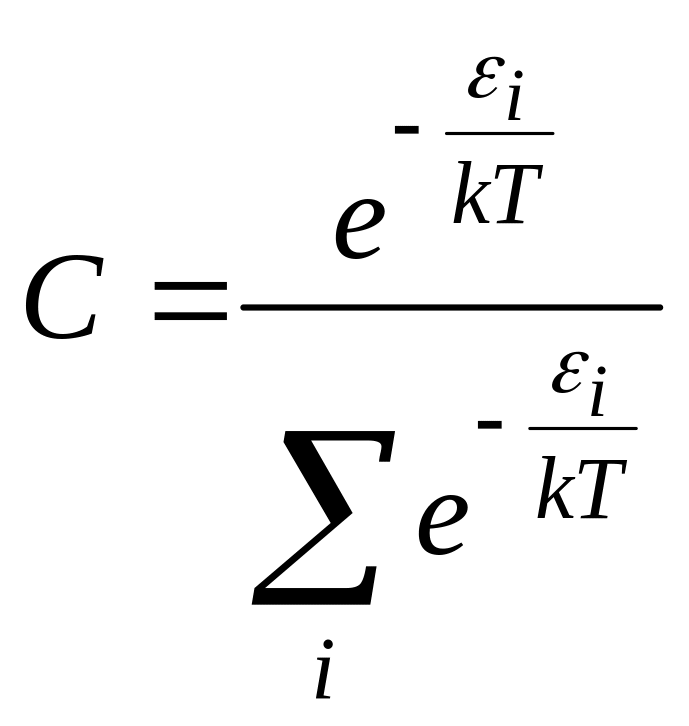 .
.
НТ1(З). Выражение
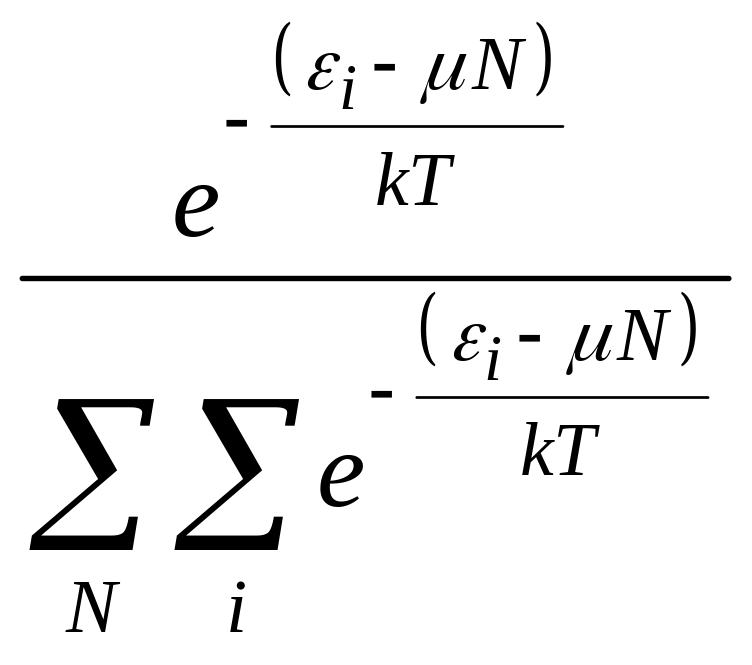 :
:
А) имеет смысл распределения частиц по энергиям;
В) равно среднему числу частиц в состоянии с энергией εi;
*С) равно вероятности встретить подсистему, состоящую из N частиц,
в состоянии с энергией εi;
D) равно нормировочному множителю в большом каноническом
распределении Гиббса.
НТ1(З).
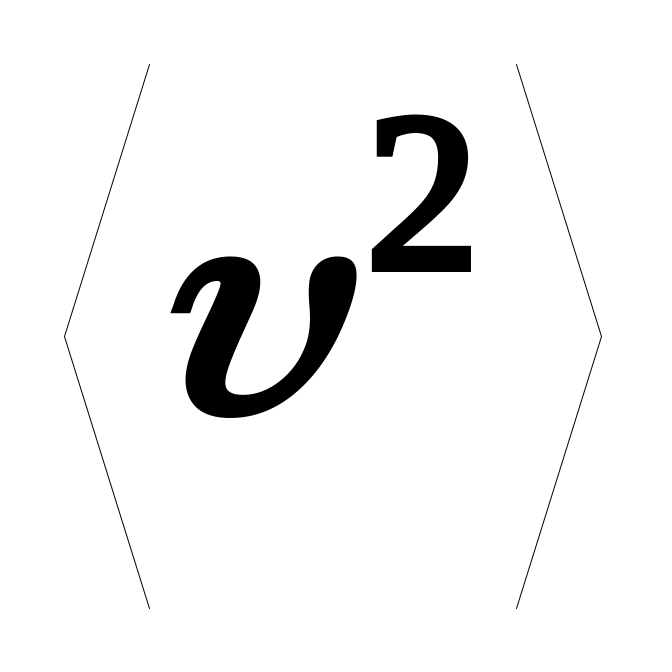 можно
найти, вычислив значение интеграла
можно
найти, вычислив значение интеграла
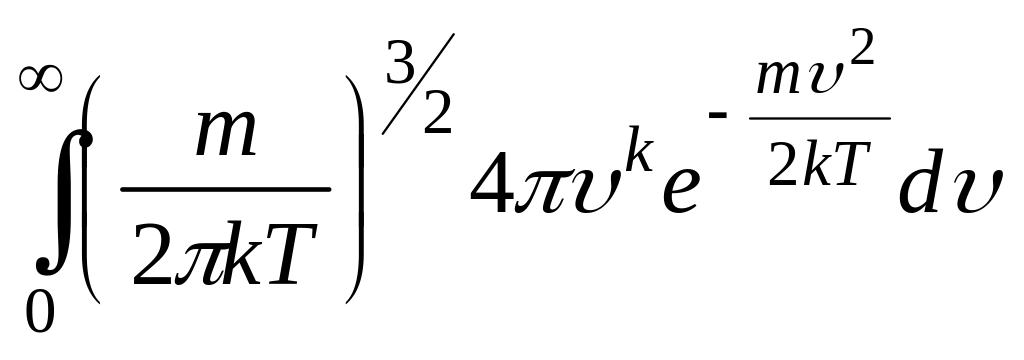 ,
где k=….
(*Ответ: 4)
,
где k=….
(*Ответ: 4)
НТ1(З). Если F(x) – плотность вероятности или функция распределения
случайной
величины
х,
то выражение
![]()
(*Ответ:<f(x)>)
НТ1(О). Интеграл
 ,
где k=….
(*Ответ: 1)
,
где k=….
(*Ответ: 1)
Нт1(з). Если f(X) – плотность вероятности или функция распределения
случайной
величины
х,
то выражение

*A)
![]() ;
;
*B)
 ;
;
C)
![]() ;
;
*D)![]() ;
;
E)
![]()
Правильные выражения:
НТ2(С). Найдите все возможные соответствия между левым и правым
столбиками. Ответ дайте в виде: k-l, m-n, …
-
а) значение интеграла равное 1;
b) среднее значение
 ;
;c) среднее значение
 .
.а)
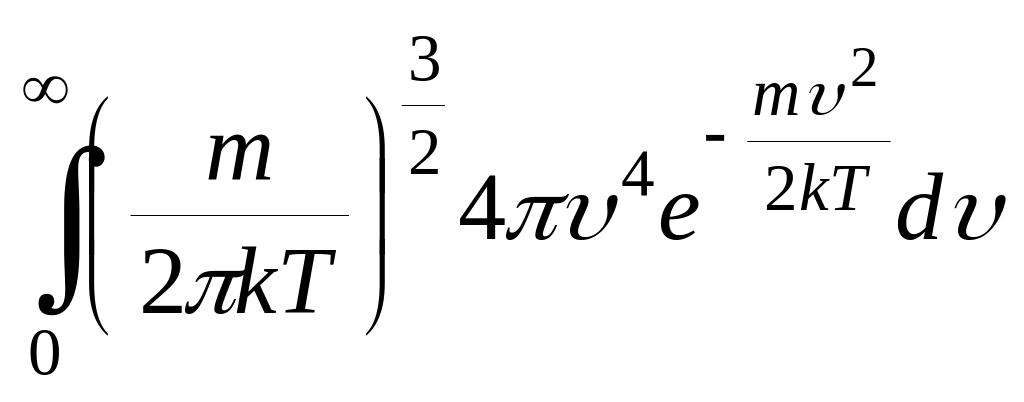 ;
;b)
 ;
;c)
 ;
;d)
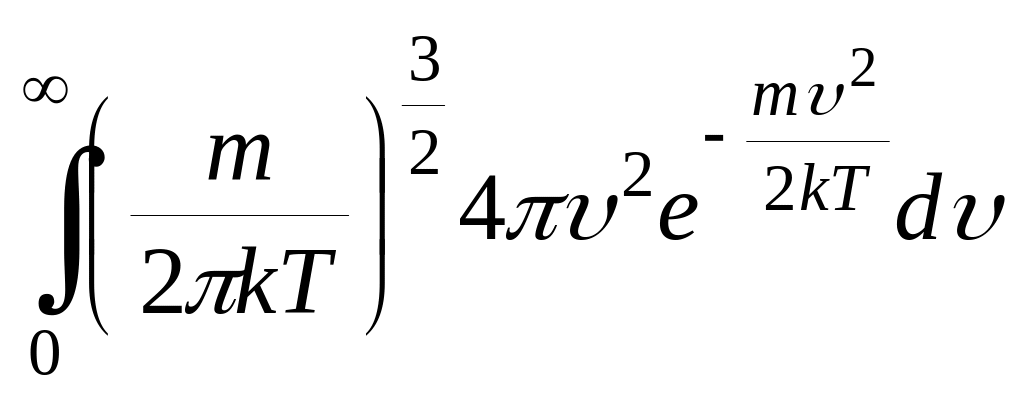 .
.
(*Ответ:a-d, c-a)
НТ1(З).Средние скорости молекул идеальных газов, у которых
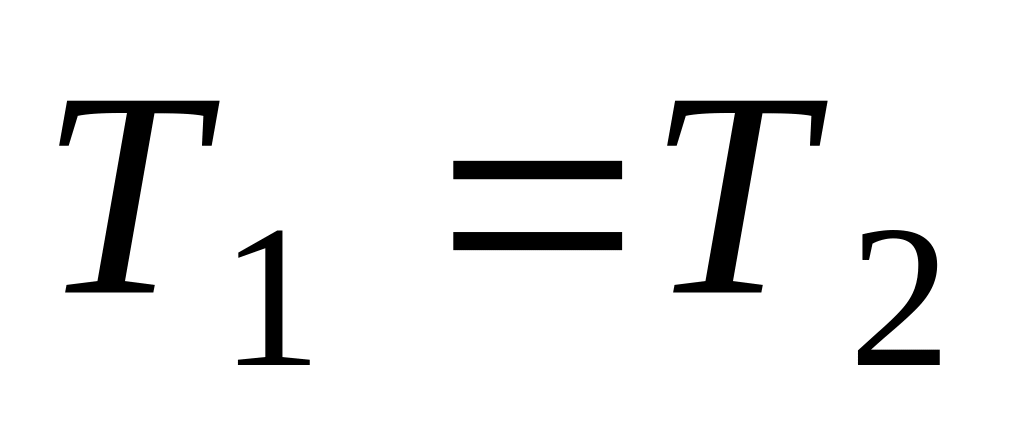 ,
а
,
а
массы
молекул
![]() >
>
![]() :
:
*А)
![]() <
<![]() ;
;
В) > ;
C) = ;
D)
![]() не
связана с их массой.
не
связана с их массой.
НТ1(З). Если число молекул идеального газа выросло в четыре раза (N2=4N1), а и
![]() ,
то относительное число молекул, имеющих
скорости от
,
то относительное число молекул, имеющих
скорости от
![]() до
до
![]() :
:
А) увеличилось в 4 раза;
В) уменьшилось в 4 раза;
*С) осталось прежним;
D) увеличилось в 2 раза.
НТ1(З). F(x) – плотность вероятности или функция распределения случайной величины х.
Среднее значение
![]() равно:
равно:
А)![]() ;
;
В)
![]() ;
;
С)
![]() ;
;
*D)
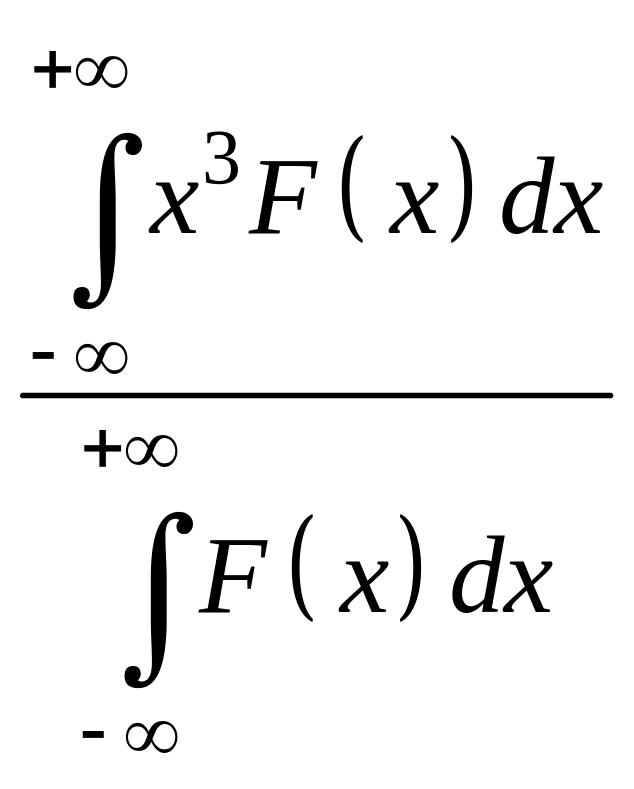 .
.
НТ1(З). f(p)- функция распределения по модулю импульса для молекул идеального газа. Среднее значение
 равно:
равно:
А)
![]() ;
;
*В)
![]() ;
;
С)
![]() ;
;
D)
![]()
НТ1(З). Молекулы идеального газа :
А) всегда имеют целый спин;
В) всегда имеют полу целый спин;
*С) могут иметь как целый, так и полу целый спин;
D) вообще не имеют спина.
НТ1(О). При одинаковых температурах наиболее вероятная скорость
молекул кислорода ……… наиболее вероятной скорости молекул водорода. Вставьте
слово.
(* меньше)
НТ1(О). При одинаковых температурах средняя квадратичная скорость молекул кислорода ………средней квадратичной скорости молекул водорода. Вставьте слово.
(* меньше)
НТ1(О). При одинаковых температурах средняя энергия молекул кислорода……… средней
энергии молекул водорода. Вставьте слово.
(*равна)
НТ1(З). Наиболее вероятное значение энергии для молекул идеального газа:
А) ~![]() ;
;
В) ~![]() ;
;
C) ~m;
*D) не зависит от m .
НТ2(О). При Т=const максимальное значение плотности вероятности
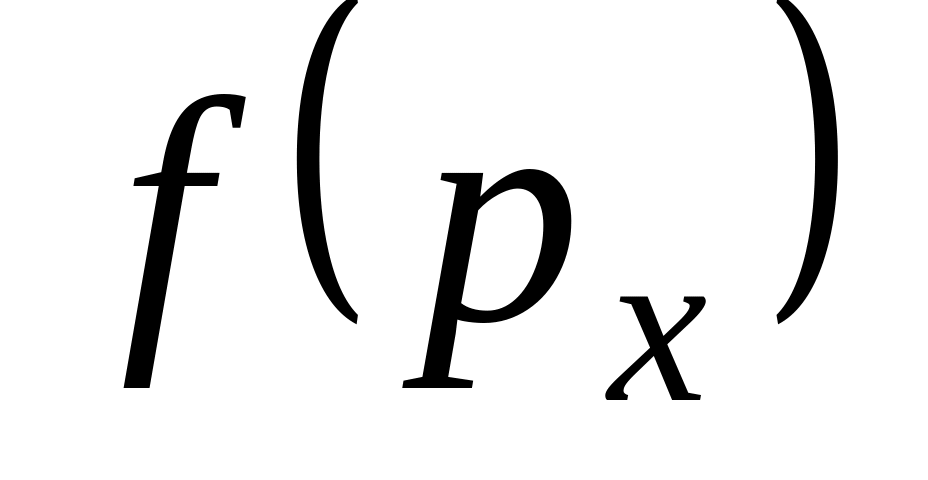 с
увеличением массы молекул ……. Вставьте
слово.
с
увеличением массы молекул ……. Вставьте
слово.
(*уменьшается)
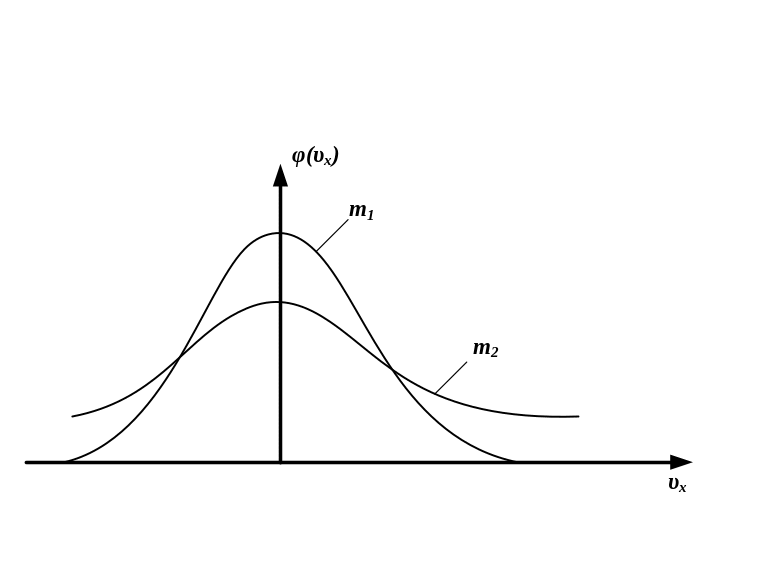
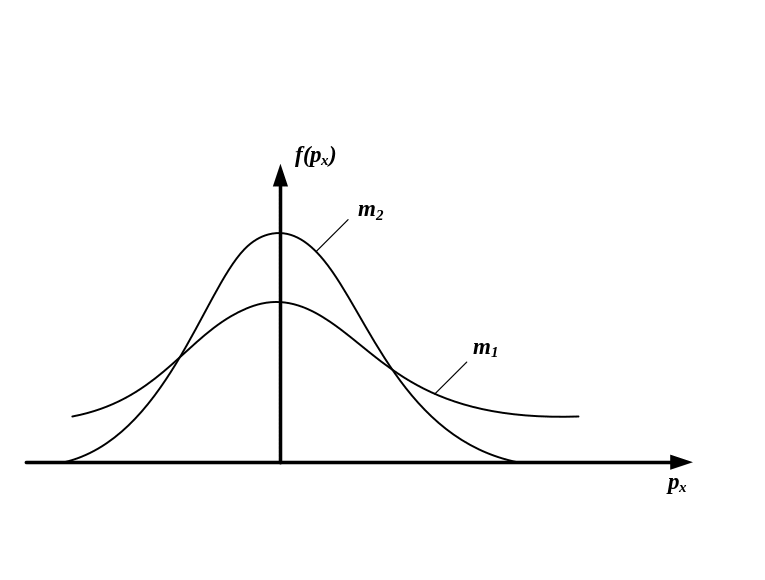
НТ1(З). В функции распределения Максвелла по проекции скорости
 m
– это:
m
– это:
*А) масса одной молекулы определенного газа;
В) общая масса газа;
С) масса одного моля;
D) некоторая масса частицы, одинаковая для всех газов.
НТ1(З). Плотность вероятности или функция распределения молекул идеального газа по проекции скорости имеет вид
 ,
где нормированный множитель C
равен:
,
где нормированный множитель C
равен:
А)
![]()
![]() ;
;
B)
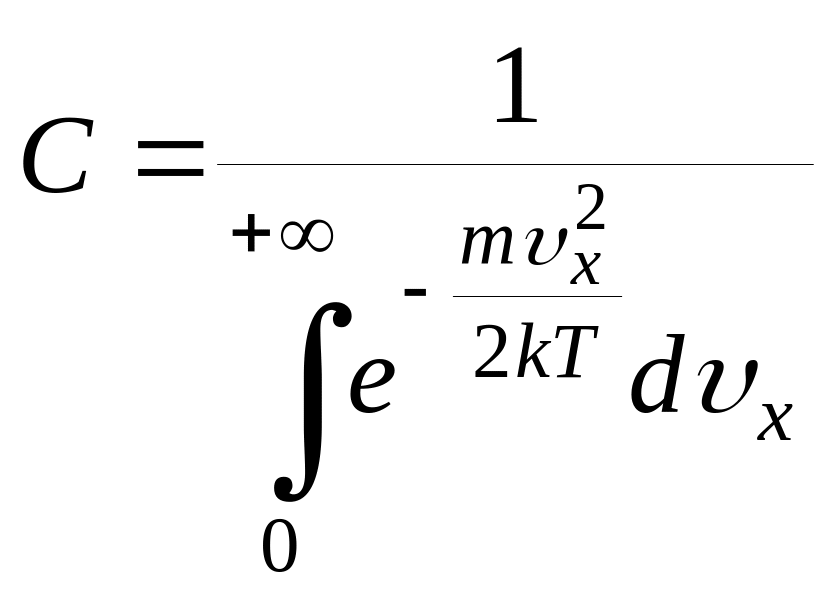 ;
;
*C)
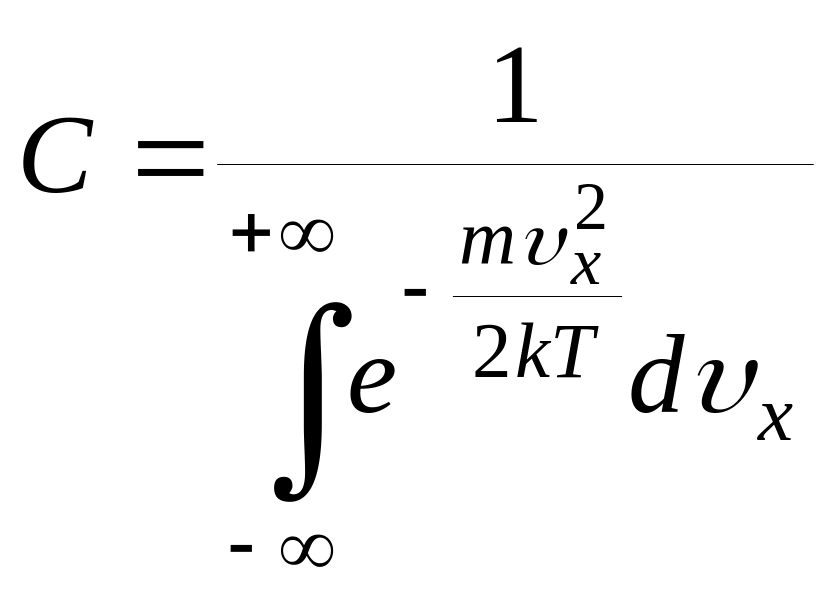 ;
;
D)
![]() .
.
НТ1(З). Значения интегралов
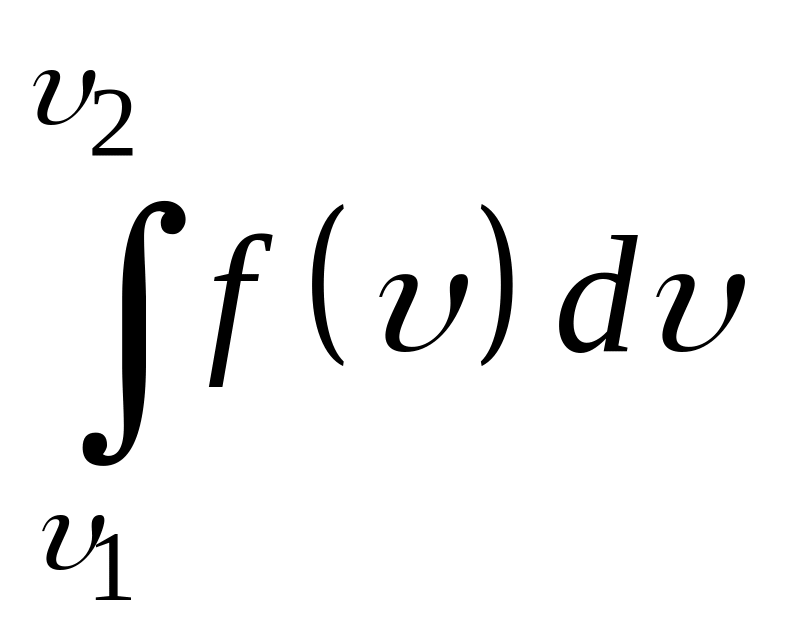 для
разных газов
для
разных газов при
при
одинаковых температурах:
А) всегда совпадают;
В) тем больше, чем больше масса одной молекулы;
С) тем больше, чем меньше масса одной молекулы;
*D) нельзя сравнить, так как значения интеграла зависят от выбранного
интервала скоростей.
-
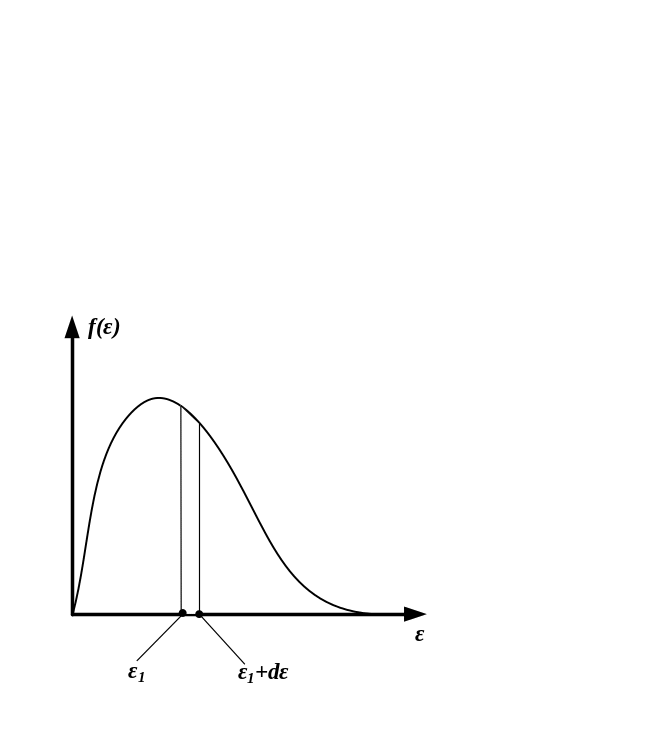
НТ1(З).
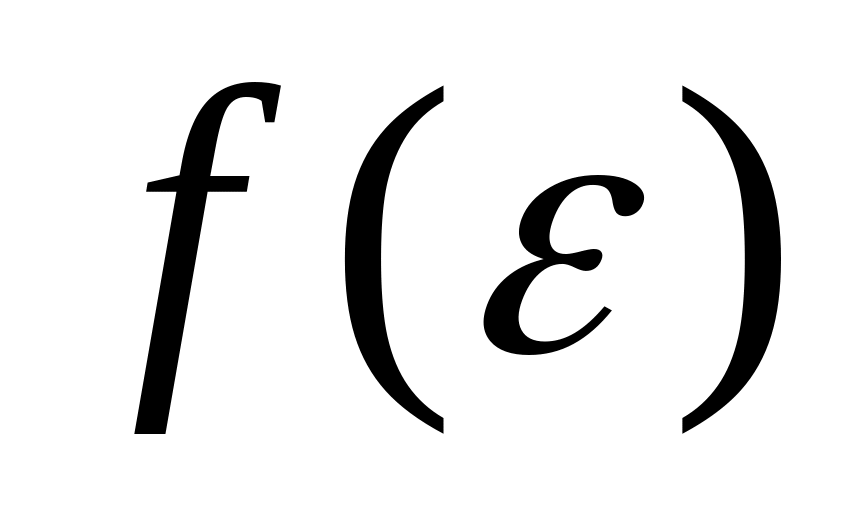 -
плотность
-
плотность
вероятности или функция распределения молекул идеального газа по энергии. Заштрихованная площадь равна:
А) общей энергии всех молекул

с энергиями от
 до
до
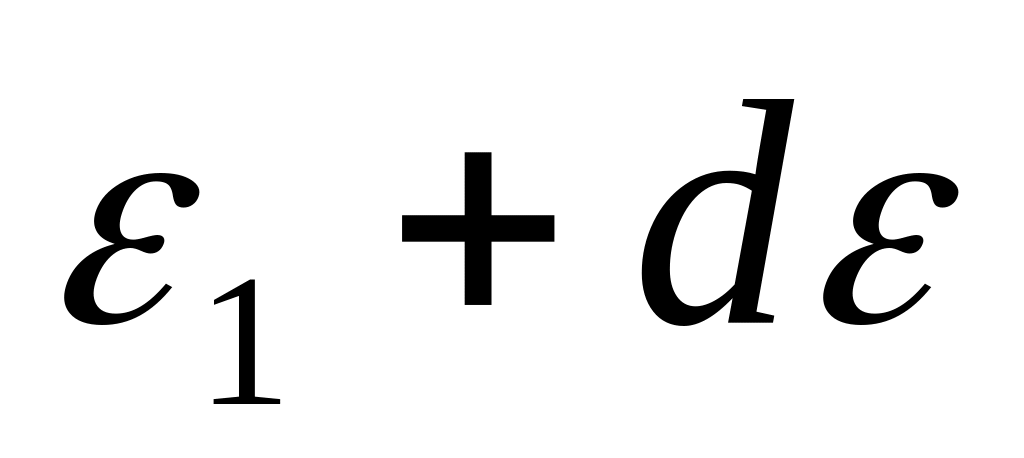 ;
;В) числу молекул
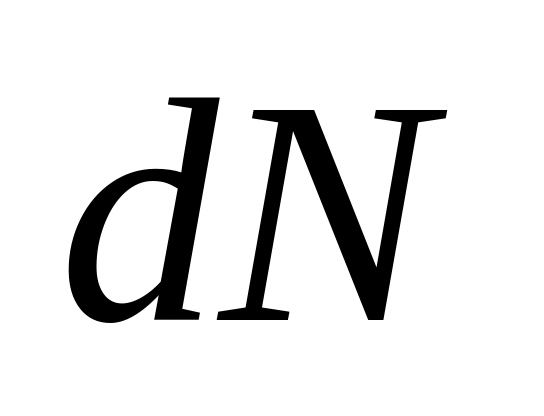 ,
имеющих
,
имеющих
энергию от до ;
С) вероятности встретить частицы с
энергией ;
*D) относительному числу молекул
 ,
имеющих энергию от
до
,
имеющих энергию от
до
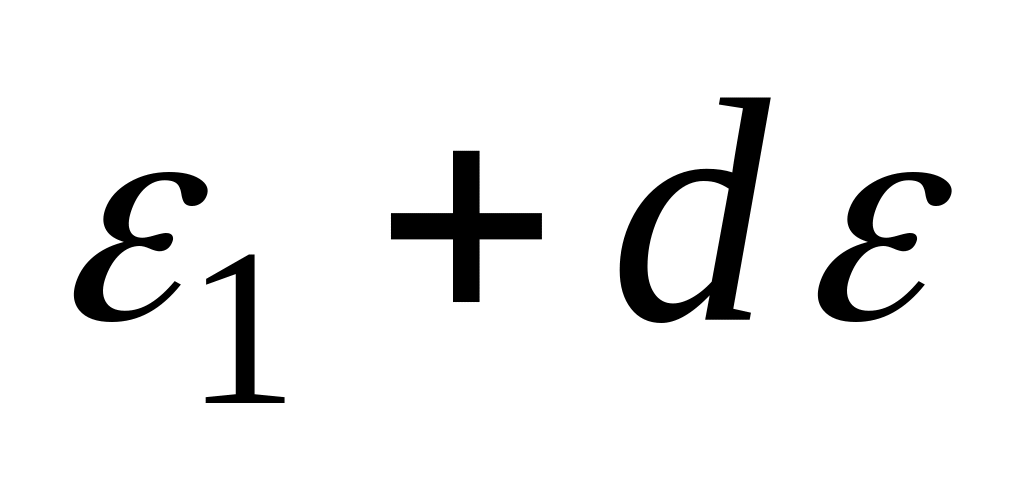 ;
;
пользуясь любым выражением, кроме …
*А)
В)
С)
D)
|
А)
*В)
С)
D) безразмерная
|
*А)
В)
С)
D)
|
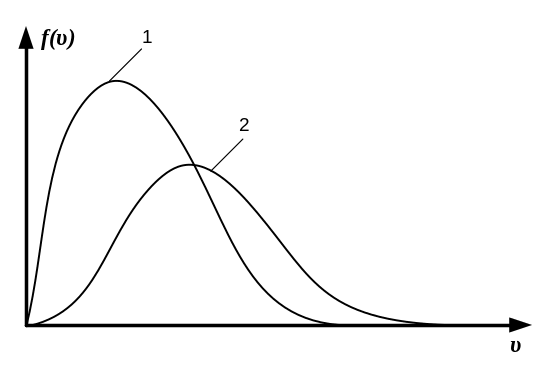
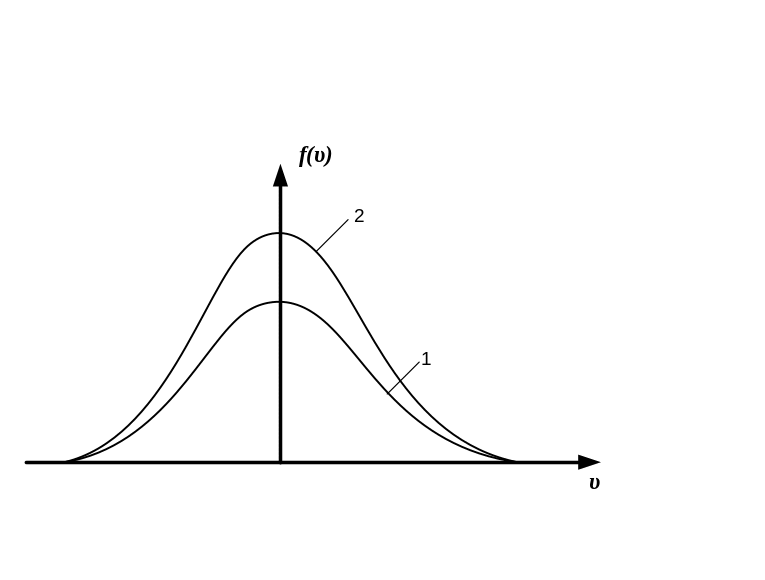
*А) S1=S2=S3=1, T3>T2>T1; B) S1=S2=S3=1, T1>T2>T3; C) S1>S2>S3, T1>T2>T3; D) S1<S2<S3, T1<T2<T3 |
А)
*В)
C)
D)
A)
B)
C)
*D)
|
А)
В)
С)
*D)
А) 1;
В)
С)
*D)
А)
*В) 0
С)
D)
А) потенциальная энергия взаимодействия молекул друг с другом плюс суммарная кинетическая энергия частиц; *В) потенциальная энергия частиц во внешнем поле плюс суммарная кинетическая энергия молекул; С) только кинетическая энергия молекул; D) только потенциальная энергия частиц во внешнем поле.
А)
*В)
С)
D)
А)
В)
*С)
D)
А) среднему
значению
на интервале от
В)
вероятности встретить частицы с
энергиями от
и
С) числу
частиц, имеющих энергию
*D) суммарной энергии всех частиц, у которых
А)
B)
*C) 0;
D)
А)
*В)
С)
|
D)
А)
B)
C)
*D)
А)
*В)
С)
D)
*A)
B)
C)
D)
А) от -∞ до ∞;
В)
*С)
D)
А)
B)
C)
*D)
А)
*В)
С)
D)
А)
*B)
C)
D)
А)
*B)
C)
D)
*А)
B)
C)
D)
А)
В)
*С)
D)
х1,
х2,
…хп,
а Рi
– вероятность появления xi,
то среднее значение
*А)
B)
C)
D)
А) 1;
В) среднему
значению
С) среднему
значению
*D) 0.
А)
В)
*С)
D)
А)
В)
*С)
D)
А) средняя скорость, где m – масса одной молекулы; В) средняя скорость, где m – молярная масса газа; С) средняя квадратичная скорость, где m – общая масса газа. *D) средняя квадратичная скорость, где m – масса одной молекулы.
A) можно, заменив p на mu в выражении f(p); *B) можно, заменив p на mu и dp на mdu в выражении f(p)dp; C) можно, выполнив любое из преобразований (А) или (В), так как получится одно и тоже выражение; D) нельзя ни одним из преобразований
пронормированная на 1, имеет вид:
А)
*В)
С)
D)
А)
В)
*С)
D)
A)
B)
*C)
D)
E)
*А)
В)
С)
D)
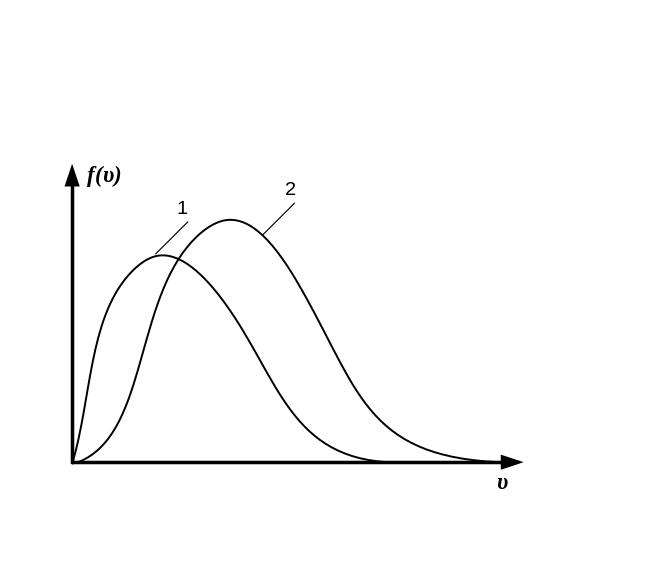
А) числу молекул с данной скоростью; В) вероятности того, что скорость молекулы равна υ; *С) *C) относительному числу молекул в единичном интервале скоростей; D) относительному числу молекул в интервале скоростей dυ
A)
B)
*C)
D)
E)
то отношение
вероятностей встретить молекулы с
энергиями от
до
(*Ответ: 1)
максимальных
значений функций распределения
k-l, m-n,…
а)
b)
с)
d)
;
;
d)
(*Ответ:a-b, b-c, c-a, d-b)
210-3кг/моль) при Т=300 К с учетом
NA»6×10231/моль
A) I1= I2; *B) I1<I2; C) I1>I2; D) нельзя сравнить, не зная температуры.
Т=const,
а u2>u1
отношение
A) всегда >1; B) всегда <1; C) >1, если u1 и u2 больше uнв - наиболее вероятной скорости; *D) >1, если u1 и u2 меньше uнв; *E) <1, если u2 и u1 больше uнв ; F) <1, если u1 и u2 меньше uнв ; G) >1, если u1<uнв<u2 . Правильные утверждения:
A)
можно, заменив
B)
можно, заменив
на
и
du
на
*C)
можно, заменив
на
и
du
на
D) можно, выполнив любое из преобразований (А) или (В), так как получится одно и тоже выражение; E) нельзя ни одним из этих преобразований.
A)
B)
C)
*D)
E)
F)
A)~
B)~
C)~
*D)~ E) не зависит от m.
(*Ответ: 9)
распределения
Т=400 К равно …. (*Ответ: 0)
(*Ответ: 420)
*A) b;
B)
C)
D)
E)
F)
|

 ;
; 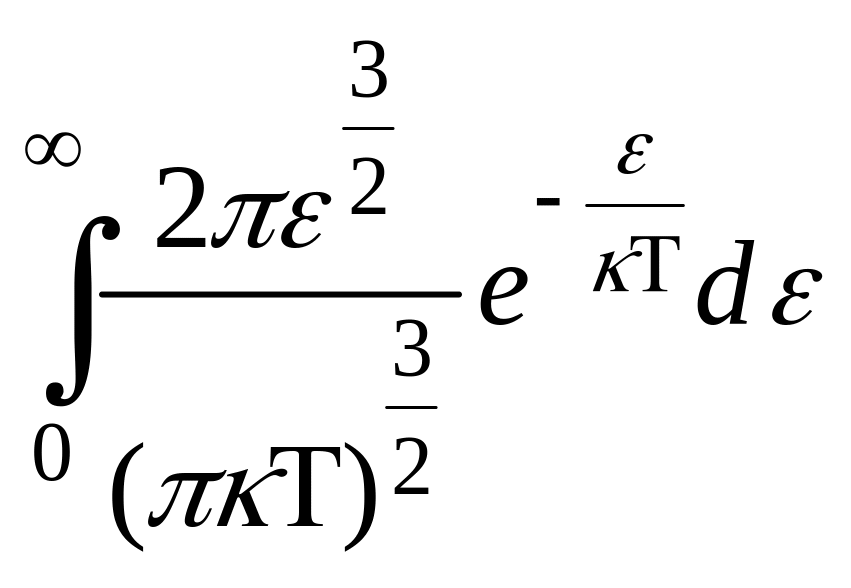 ;
; ;
;
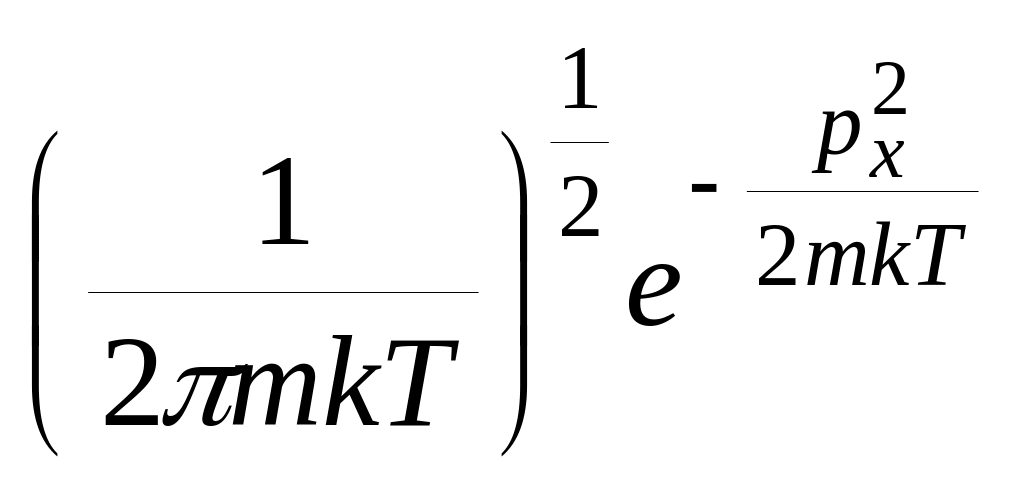 является:
является: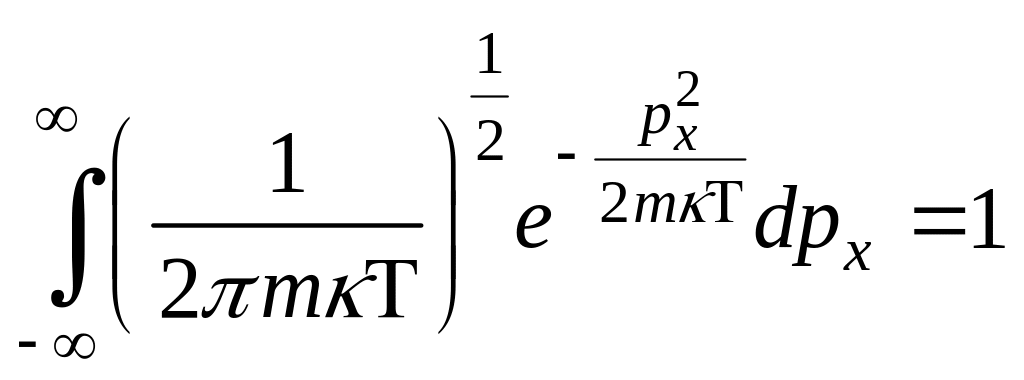

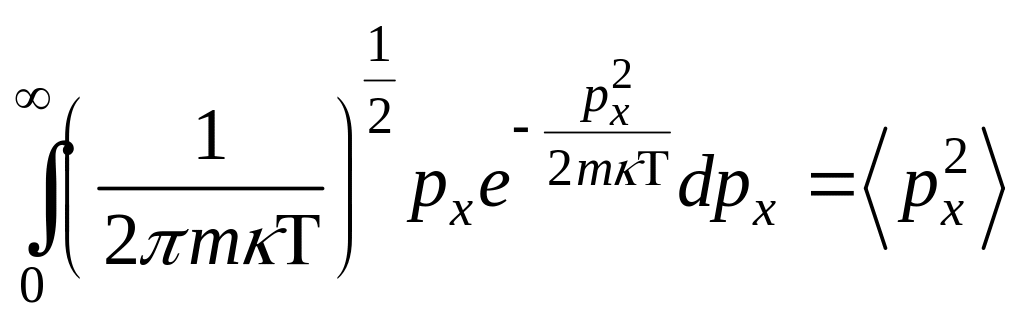


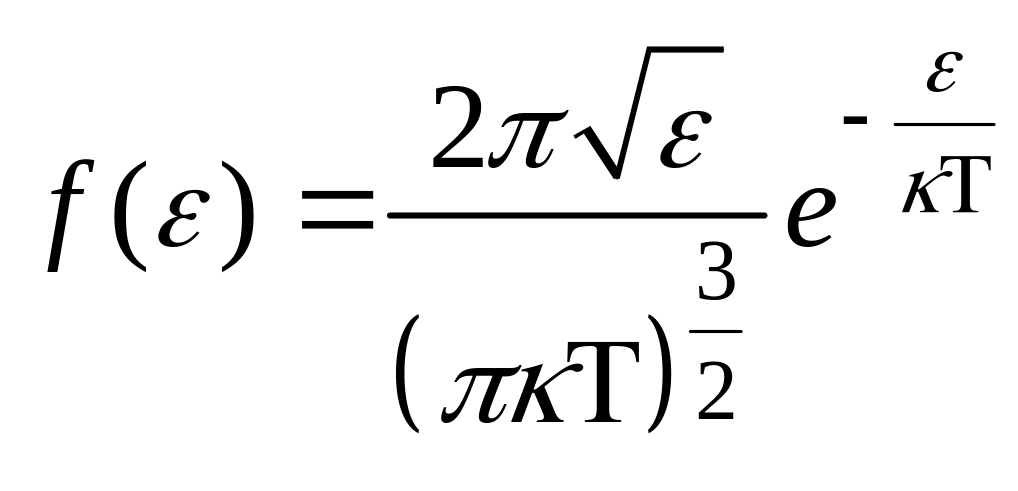 - плотность вероятности или функция
распределения молекул идеального
газа по энергии. Среднее значение
- плотность вероятности или функция
распределения молекул идеального
газа по энергии. Среднее значение
 ;
;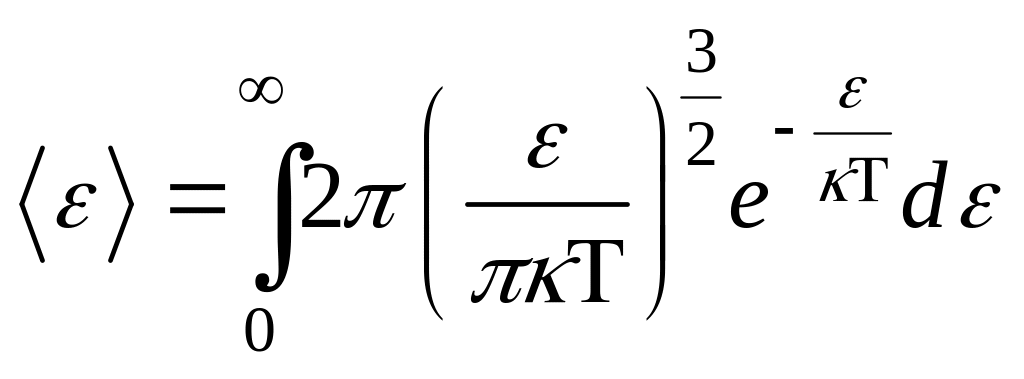 ;
; ;
; ,
где N
– число частиц.
,
где N
– число частиц. ;
;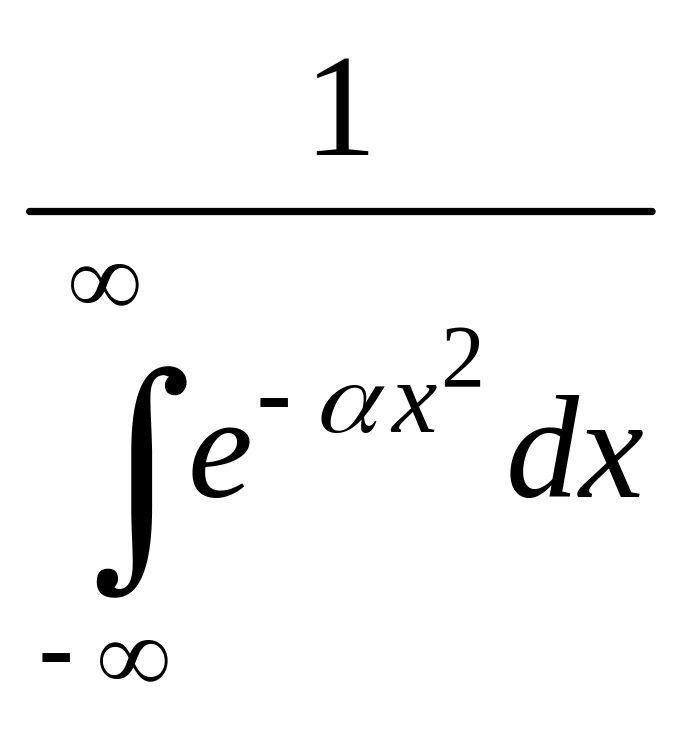 .
. равен:
равен: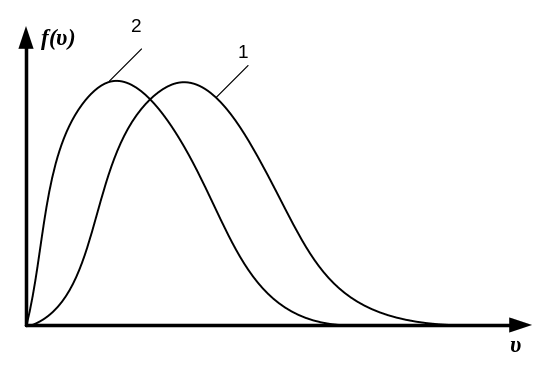





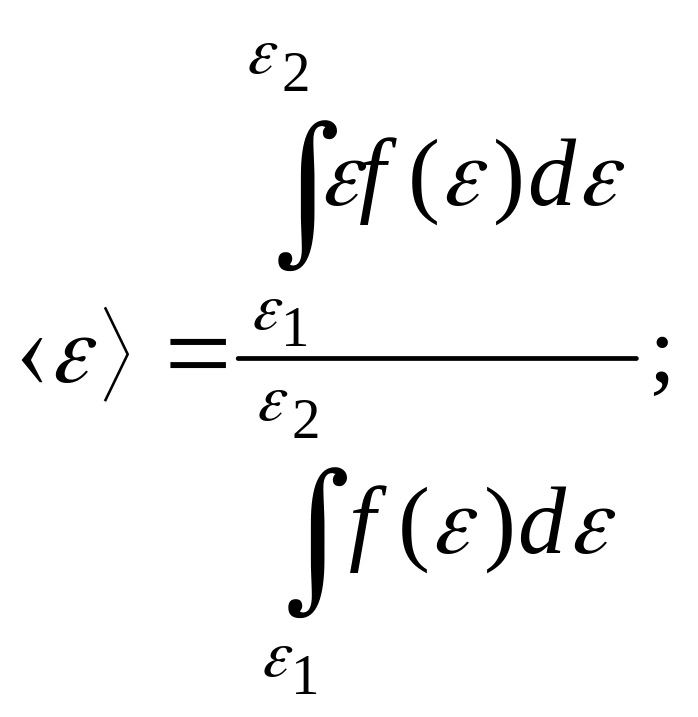
 ;
;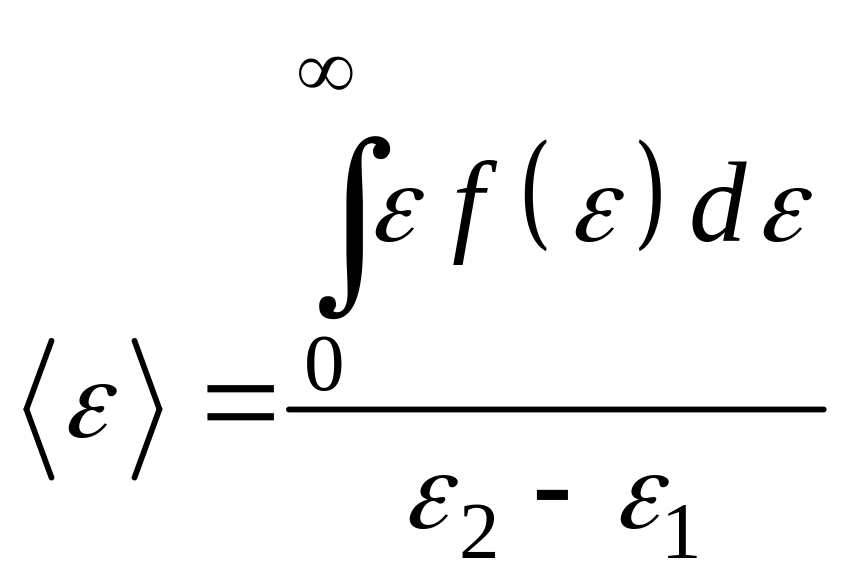 ;
;
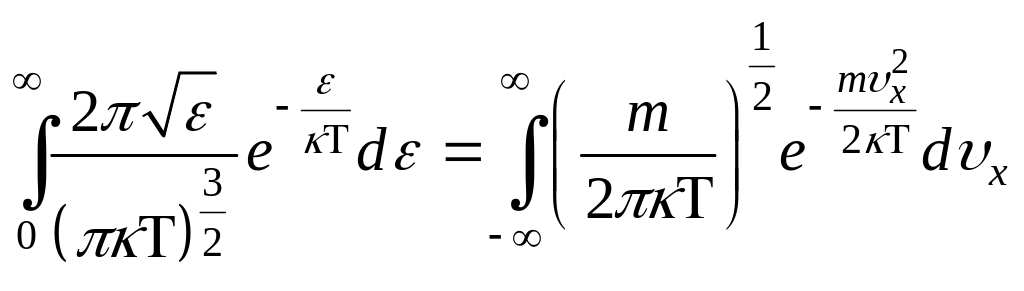 ;
;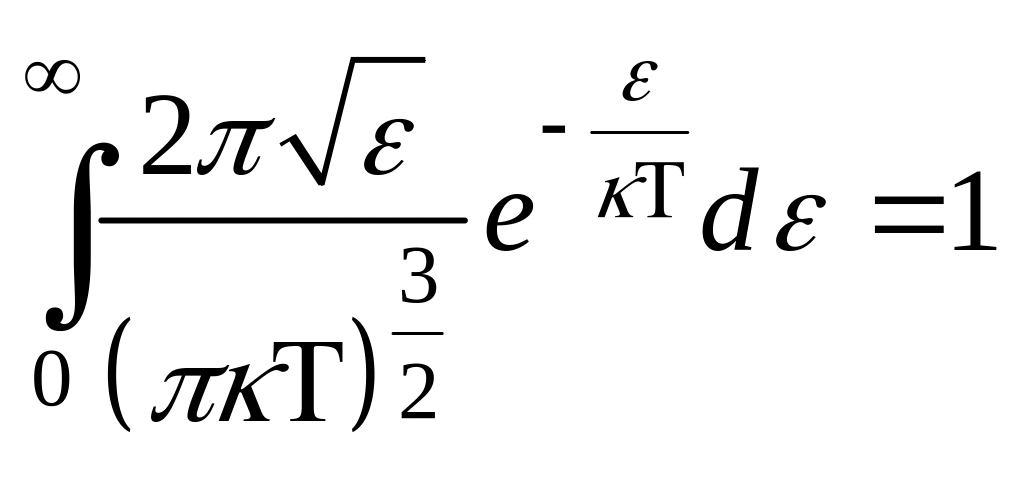 ;
; ;
;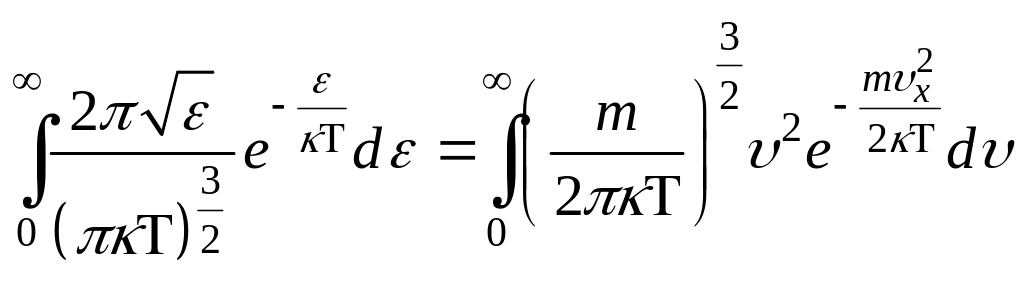 .
.


 ;
; ;
; ;
;
 ;
;
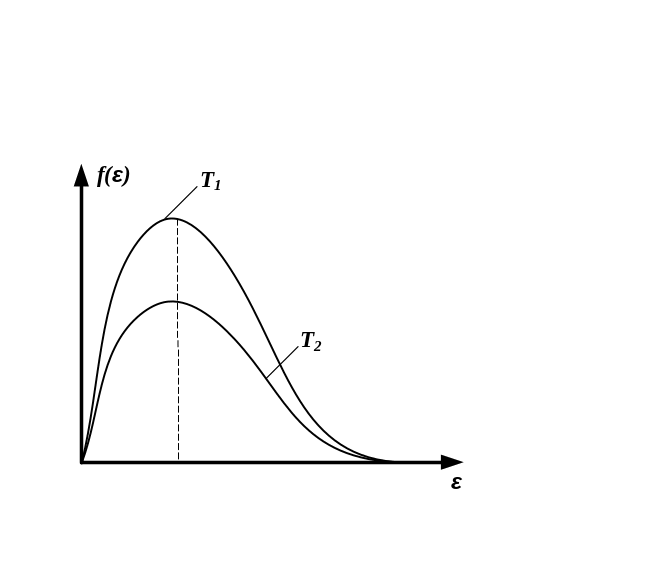
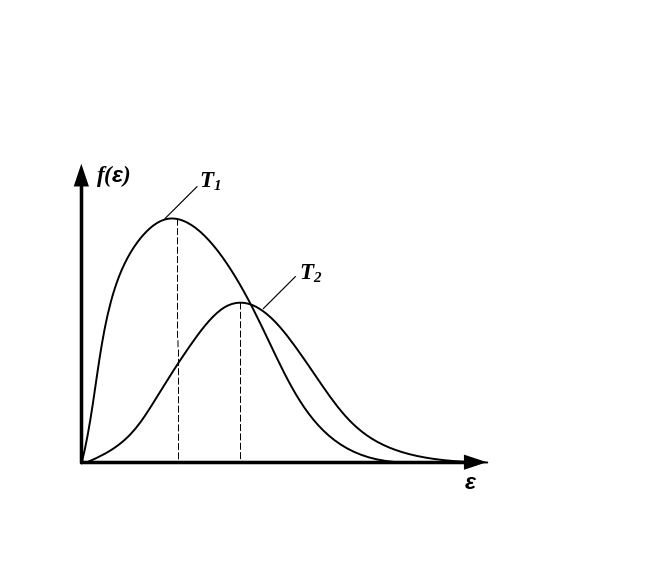
 ;
;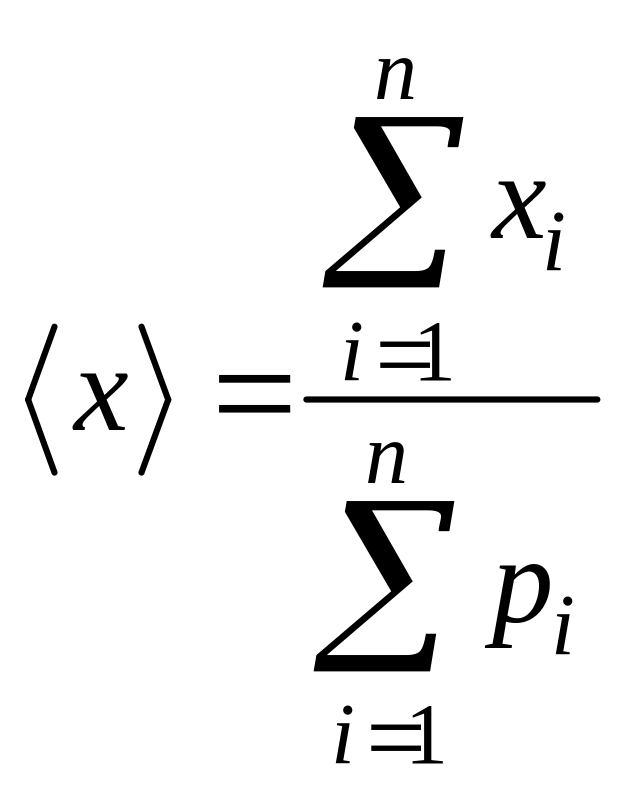
 равно:
равно: ;
; ;
;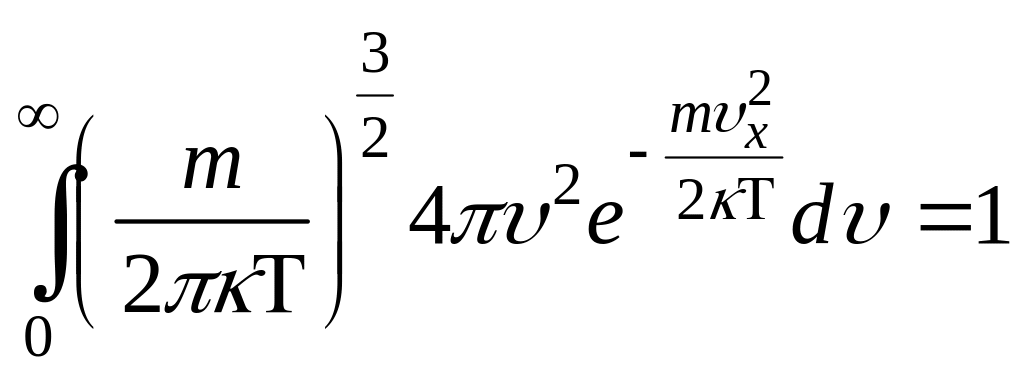 ;
;

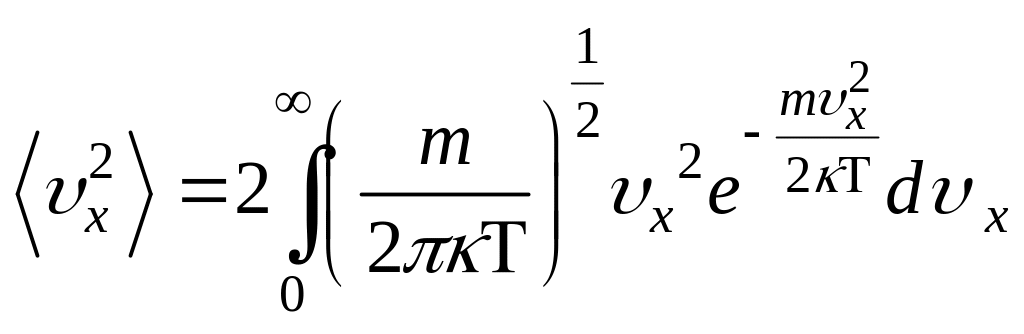 ;
; ;
; ;
;
 к функции
распределения по модулю скорости
f(u):
к функции
распределения по модулю скорости
f(u):

 ,
где A
и B
– целые числа, значения которых
перечислите через точку с запятой …
, … без учета размерностей. (*Ответ:
5; -19)
,
где A
и B
– целые числа, значения которых
перечислите через точку с запятой …
, … без учета размерностей. (*Ответ:
5; -19)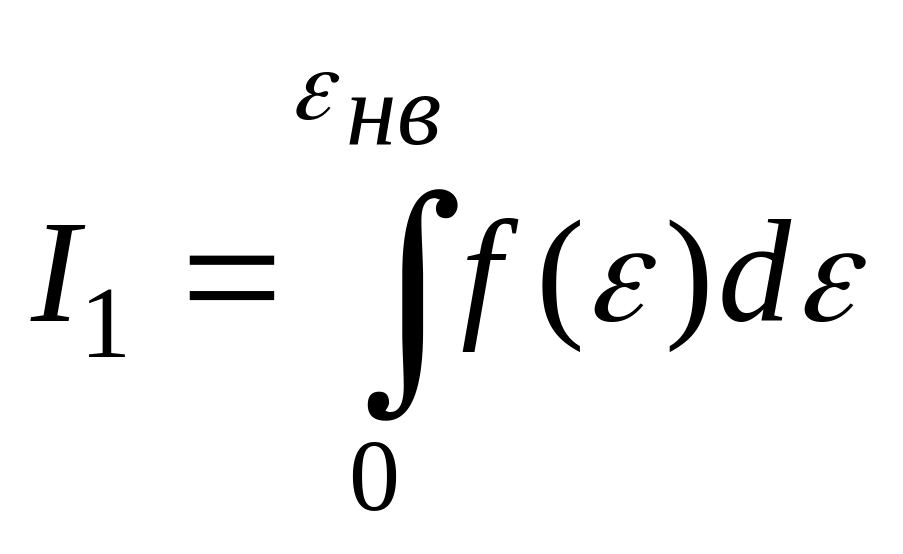 и
и