12. Стійка рівновага у «павутиноподібній» моделі. Умови існування стійкої рівноваги у «павутиноподібній» моделі.

«павутиноподібна» модель – це модель, що описує процес формування попиту і пропозиції певного товару чи виду послуг на конкурентному ринку (за умов досконалої конукренції).

Розглядаючи «павутиноподібну» модель, приймають гіпотезу, що функції пропозиції і попиту залежать лише від ціни товару:

, ,

де — кількість товару, яку товаровиробники доставляють на ринок, тобто пропозиція; — деяка монотонно зростаюча функція; — кількість товару, який можна продати на ринку, тобто попит; — деяка монотонно спадна функція.

Графіки попиту і пропозиції перетинаються у точці рівноваги, а ціна, що відповідає цій точці , і є рівноважною ціною. Враховуючи властивості кривих попиту і пропозиції, рівноважний розв’язок є стійким у тому сенсі, що якщо ціна строго фіксована і рівна рівноважній ціні, то товаровиробник, максимізуючи прибуток, доставляє на ринок товар у кількості ; одночасно споживач, що намагається максимізувати свою функцію корисності, формує попит . При встановленні рівноважної ціни на ринку досконалої конкуренції кількість товару, що пропонується товаровиробником за цією ціною, дорівнює попиту споживача:

.

Рівноважний стан «павутиноподібної» моделі буде стійким, якщо існують границі:

де — рівноважна ціна.

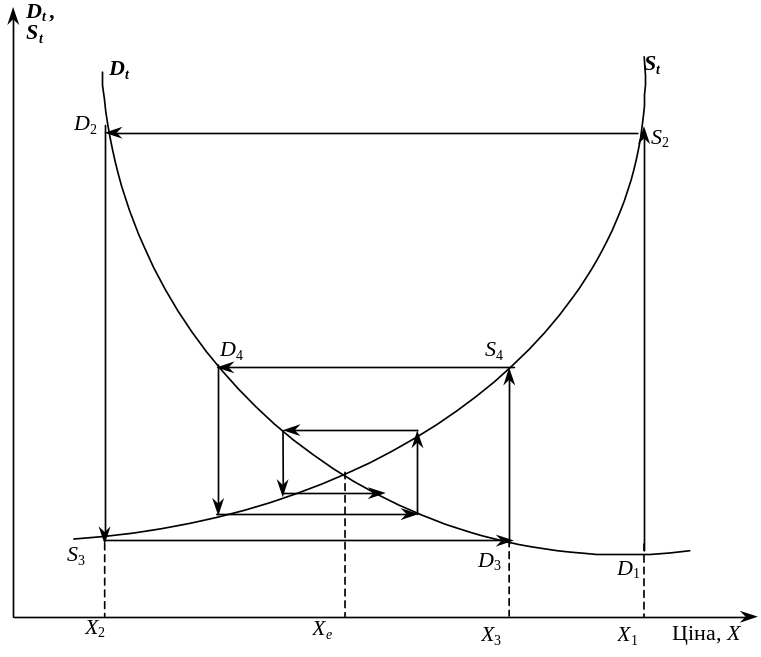
Математичні співвідношення, що відображають закон попиту — пропозиції, можуть бути проілюстровані рис. 2.2.2.

Г

Ціна, X

рафік формування попиту — пропозиції

13. Постановка задачі економіко-математичного моделювання. Сутність понять: «параметри», «змінні», «цільова функція», «система обмежень», «оптимальний план».

Подамо схематично довільну економічну систему у такому вигляді:

Параметри с_k (k = 1, 2, ..., l) є кількісними характеристиками системи.

Частина параметрів с_k для певної системи може бути сталими величинами, а частина — змінними, тобто залежатиме від певних умов.

Змінні величини бувають незалежними чи залежними, дискрет­ними чи неперервними, детермінованими або випадковими.

Вхідні змінні економічної системи бувають двох видів: керовані x_j (j=1,2,...,n), значення яких можна змінювати в деякому інтервалі; і некеровані змінні y_i (і=1,2, ..., m), значення яких не залежать від волі людей і визначаються зовнішнім середовищем. Залежно від реальної ситуації керовані змінні можуть переходити у групу некерованих і навпаки.

Кожна економічна система має певну мету свого функціонування. Ступінь досягнення мети, здебільшого, має кількісну міру, тобто може бути описаний математично.

Нехай F – вибрана мета (ціль). За цих умов вдається, як правило, встановити залежність між величиною F, якою вимірюється ступінь досягнення мети, вхідними змінними та параметрами системи:

F = f (x₁, x₂, ..., x_n; y₁, y₂, ..., y_m; c₁, c₂, ..., c_l). (1)

Функцію F наз. цільовою функцією. Для екон. с-ми це є ф-ія ефективності її функціонування та розвитку, оскільки значення F відображує ступінь досягнення певної мети.

У заг. вигляді задача економіко-матем.модел-ня формулюється так:

Знайти такі значення керованих змінних x_j, щоб цільова функція набувала екстремального (максимального чи мінімального значення).

Отже, потрібно відшукати значення

.(2)

Можливості вибору x_j завжди обмежені зовнішніми щодо с-ми умовами, параметрами виробничо-екон.ї с-ми тощо.

Ці процеси можна описати системою математичних рівностей та нерівностей виду:

(3)

Тут набір символів ( , =, ) означає, що для деяких значень поточного індексу і виконуються нерівності типу , для інших – рівності (=), а для решти – нерівності типу .

С-ма (3) наз. системою обмежень задачі. Вона описує внутрішні технологічні та екон. процеси функціонування й розвитку виробничо-економіч­ної системи, а також процеси зовнішнього середовища, які впливають на результат діяльності системи. Для економічних систем змінні x_j мають бути невід’ємними:

. (2.4)

Залежності (2)—(4) утворюють економіко-математичну модель економічної системи. Розробляючи таку модель, слід дотримуватись певних правил:

1. Модель має адекватно описувати реальні технологічні та економічні процеси.

2. У моделі потрібно враховувати все істотне, суттєве в досліджуваному явищі чи процесі, нехтуючи всім другорядним, неістотним у ньому.

3. Модель має бути зрозумілою для користувача, зручною для реалізації на ЕОМ.

4. Необхідно, щоб множина змінних x_j була не порожньою.

План, за якого цільова функція набуває екстремального значення, наз-ся оптимальним. Оптимальний план є розв’яз­ком задачі економіко-математичного моделювання (2)—(4).