5.Условная вероятность. Независимость событий.
Часто
интересует вероятность появления
события А после того, как некот.событие
В уже произошло. Такую вероятность
наз.условной и обознач.P(A/B)
и вычисляют по формуле
Аналогично, условная вероятность события B при условии, что событие A уже произошло, вычисляется
.
Из
вышепредложенных формул следует
теорема
умножения:Вероятность
произвед.2ух произвольных событий равна
произвед.вероятности одного из событий
на условную вероятность второго, при
условии, что первое уже произошло.
.
Распространим
теорему умножения на конечное число
событий:Вероятность
совместного появления нескольких
произвольных событий равна произвед.
вероятности одного из них на условные
вероятности всех остальных, причем
вероятность каждого последующего
события вычисляется в предположении,
что все предыдущие события уже произошли:
.
События
А и В наз.независимыми,если
вероятность их произвед. равна произведению
вероятностей этих событий.
.
Сравнивая формулы P(AB)=P(A)P(B/A)=P(B)P(A/B) и ,
получим
:
.
Следовательно,
для независимых событий условная и
безусловная вероятности совпадают
.
Для
конечного числа попарно независимых
событий вероятность произведения
событий равна произведению вероятностей
каждого из событий
.
6.Формула полной вероятности. Формула Байеса.
Пусть событие А может произойти только с одним из n несовместных событий H1…Hn, образующих полную группу:
Ø,
,
тогда
.
Так
как события
и
несовместны, то и (
)
и (
)
являются несовместными. Тогда по теореме
сложения
.
Применяя
теорему умножения к каждому слагаемому,
получим формулу
полной вероятности:
.
События H1, H2,…, Hn часто называют гипотезами.
Иногда
интересует, как перераспределятся
вероятности
гипотез
после того, как событие А уже произошло:
.
По теореме умножения
,
.
Подставляя в знаменатель формулу полной вероятности, получим формулу Байеса:
.
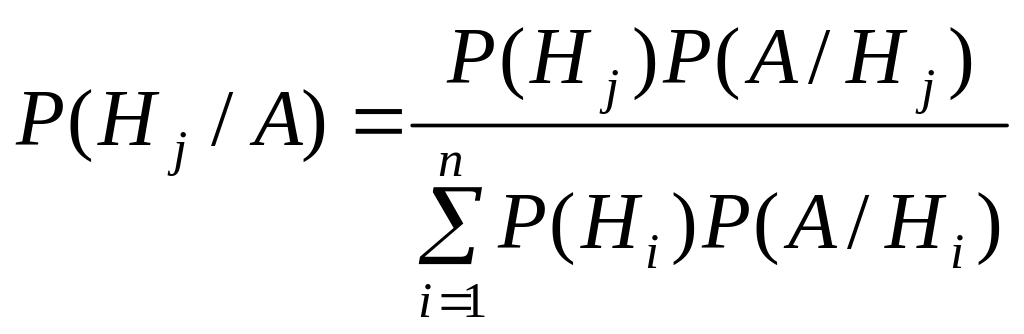7.Схема независимых испытаний Бернулли.
Пусть производится последовательность независимых испытаний, в каждом из которых возможно только 2 исхода: событие А или появится или не появится.
Обозначим
вероятность появления события
,
не появления
,
.
Под элементарным событием в схеме Бернулли понимается последовательность наступлений и не наступлений события А в n испытаниях.
Обозначим А={1}, ={0}. Тогда элементарный исход можно представить в виде вектора, состоящего из нулей и единиц, например (1,0,…, 1).
Состоящего из нулей и единиц, например (1,0,…, 1).
Найдем вероятность того, что в n испытаниях событие А появится ровно m раз.
Вычислим сначала вероятность того, что в 3-х испытаниях событие А появится 2 раза при условии, что вероятность наступления А в одном испытании равна p. При этом возможны следующие элементарные исходы:
(1,1,0); (0,1,1); (1,0,1).
Вероятность каждого элементарного исхода одинакова и равна p2q. Таким образом, вероятность того, что в 3-х испытаниях событие наступит 2 раза
.
Для произвольных m и n вероятность одного элементарного исхода равна pmqn-m . Число таких элементарных исходов равно числу способов разместить m единиц по n местам, а это по определению есть число сочетаний из n элементов по m. Получим формулу Бернулли
.
Часто в схеме Бернулли интересует вероятность появления события А не ровно m раз, а от m1 до m2 раз включительно.Тогда она определяется формулой:
