12. Стационарные точки. I достаточное условие экстремума.

ОПР1: Точки, в которых производная функции Y=f(x) равна 0, называются стационарными точками.

Каждая стационарная точка – точка возможного экстремума.

ТЕОР1: Пусть функция f(x) дифференцируема в некоторой  – окрестности точки X0. Тогда, если f ’(x)>0 (f ’(x)<0) для x(X0 - ; X0) и f ’(x)<0 (f ’(x)>0) для x(X0; X0 + ) то в точке X0 функция f(x) имеет локальный максимум (минимум), если же f ’(x) во всей  – окрестности точки X0 имеет один и тот же знак, то в точке X0 локального экстремума нет.

Док-во: Путь f ’(x) при переходе через точку X0 меняет знак с “ + ” на “ - ” и пусть x(X0 - ; X0). Применим формулу Лагранжа к функции f(x) на отрезке [x, X0]. Получаем f(X0) – f(x) = f ’(C)  (X0 - x), где C(x, X0). Так как f ’(x) >0 на (X0 - ; X0), то f ’(C) >0, и, кроме того, X0 – x >0  f(X0) - f(x) >0 или f(X0) >f(x).

Рассмотрим теперь случай, когда x(X0; X0 + ). Применим формулу Лагранжа к функции f(x) на отрезке [X0, x]. Получаем f(x) – f(X0) = f ’(C)  (x - X0), где C(X0, x). Так как f ’(x)< 0 на (X0; X0 + ), то f ’(C)< 0, и, кроме того, X0 – x < 0  f(x) - f(X0) < 0 или f(X0) >f(x).

Из неравенств следует, что в рассматриваемой окрестности точки X0 выполняется неравенство f(X0) >f(x) при X0  x, а это означает, что в точке X0 функция f(x) имеет локальный максимум. (Минимум аналогично)

Случай, когда знак не меняется. Пусть f ’(x) >0 в некоторой окрестности (X0 - ; X0 + ); тогда (по Т о монотонности Ф) функция f(x) возрастает на (X0 - ; X0 + ), т. е. для x< X0 выполняется неравенство f(X0) >f(x), а для x >X0 - f(X0)< f(x). Это означает, что точка не является точкой локального экстремума.

12. Достаточное условие экстремума.

ТЕОР1: Пусть функция f(x) дифференцируема в некоторой  – окрестности точки X0. Тогда, если f ’(x)>0 (f ’(x)<0) для x(X0 - ; X0) и f ’(x)<0 (f ’(x)>0) для x(X0; X0 + ) то в точке X0 функция f(x) имеет локальный максимум (минимум), если же f ’(x) во всей  – окрестности точки X0 имеет один и тот же знак, то в точке X0 локального экстремума нет.

Док-во: Путь f ’(x) при переходе через точку X0 меняет знак с “ + ” на “ - ” и пусть x(X0 - ; X0). Применим формулу Лагранжа к функции f(x) на отрезке [x, X0]. Получаем f(X0) – f(x) = f ’(C)  (X0 - x), где C(x, X0). Так как f ’(x) >0 на (X0 - ; X0), то f ’(C) >0, и, кроме того, X0 – x >0  f(X0) - f(x) >0 или f(X0) >f(x).

Рассмотрим теперь случай, когда x(X0; X0 + ). Применим формулу Лагранжа к функции f(x) на отрезке [X0, x]. Получаем f(x) – f(X0) = f ’(C)  (x - X0), где C(X0, x). Так как f ’(x)< 0 на (X0; X0 + ), то f ’(C)< 0, и, кроме того, X0 – x < 0  f(x) - f(X0) < 0 или f(X0) >f(x).

Из неравенств следует, что в рассматриваемой окрестности точки X0 выполняется неравенство f(X0) >f(x) при X0  x, а это означает, что в точке X0 функция f(x) имеет локальный максимум. (Минимум аналогично)

Случай, когда знак не меняется. Пусть f ’(x) >0 в некоторой окрестности (X0 - ; X0 + ); тогда (по Т о монотонности Ф) функция f(x) возрастает на (X0 - ; X0 + ), т. е. для x< X0 выполняется неравенство f(X0) >f(x), а для x >X0 - f(X0)< f(x). Это означает, что точка не является точкой локального экстремума.

ТЕОР2: Пусть функция f(x) имеет в данной стационарной точке C конечную производную. Тогда функция f(x) имеет в точке C локальный максимум, если f ’’(x) < 0 и локальный минимум, если f(x) > 0.

Док-во: Для максимума.

Р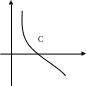 ассмотрим функцию f ’(x). Так как C стационарная точка, то f ’(C) = 0. Так как f ’’(C) < 0, т. е. (f ’(x))’ < 0, то (из достаточного условия возрастания и убывания функции в точке), что f ’(x) убывает в точке C. График функции f ’(x) имеет вид. Тогда существует такая окрестность точки, в пределах которой f ’(x) слева от точки C и f ’(x) справа от точки C. Но тогда выполняется первое достаточное условие экстремума, и функция f(x) имеет в точке C локальный максимум. (Минимум аналогично)