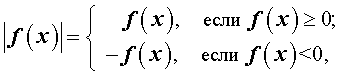- •§ 3. Основные свойства определителей 3-го порядка.
- •Тогда, используя свойство 5, а затем 4, будем иметь
- •Свойства обратной матрицы
- •Матричный метод решения систем линейных уравнений
- •Алгоритм
- •[Править] Пример
- •Компланарные векторы
- •Бесконечно малая величина
- •[Править] Бесконечно большая величина
- •Предел последовательности и функции. Теоремы о пределах
- •Бесконечно малые функции
- •Свойства бесконечно малых функций
- •Бесконечно большие функции
- •Свойства бесконечно больших функций в точке
- •Пределы функции на бесконечности
- •Определения Править
- •Окрестностное определение Править
- •Определения Править
- •Определения
- •[Править] Односторонний предел по Гейне
- •[Править] Односторонний предел по Коши
- •[Править] Односторонний предел как предел вдоль фильтра
- •[Править] Обозначения
- •Построение асимптот при анализе функций
- •Примеры:
- •Точки разрыва
- •Непрерывность функции в точке
- •Свойства непрерывных функций
- •Свойства непрерывных функций. Непрерывность сложной функции
- •Теоремы о непрерывных функциях
- •Непрерывность обратной функции
- •Непрерывность функций
- •[Править] Доказательство
- •Формулировка
- •[Править] Доказательство для r
- •[Править] Замечания
- •Второй замечательный предел
- •Натуральные логарифмы
- •Свойства Править
- •Дифференцирование сложной функции
- •[Править] Примеры
- •[Править] Свойства
- •[Править] Разложение в степенной ряд
- •Теорема об обратной функции.
- •Теорема (о дифференцировании обратной функции)
- •Примеры
- •Дифференцирование функций заданных параметрически
- •36. Логарифмическое дифференцирование.
- •Правила отыскания производных показательных и логарифмических функций.
- •Производные обратных тригонометрических функций
- •Теорема Ролля
- •Геометрический смысл теоремы Ролля
- •Теорема Лагранжа
- •Геометрический смысл теоремы Лагранжа
- •Теорема Коши
Компланарные векторы
О![]() пределение 9.10.
пределение 9.10.
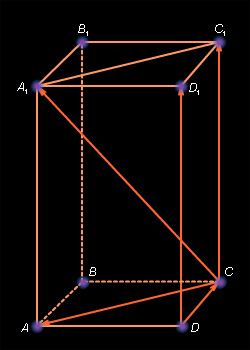
Векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости.
Любые два вектора компланарны. Любые три вектора, среди которых есть два коллинеарных, компланарны.
|
Рисунок 9.2.1 |
На
рисунке 9.2.1 векторы ![]()
![]() и
и ![]() компланарны,
так как, если отложить от точки C вектор
компланарны,
так как, если отложить от точки C вектор ![]() то
все три вектора
и
то
все три вектора
и ![]() окажутся
лежащими в одной плоскости. Векторы
окажутся
лежащими в одной плоскости. Векторы ![]()
![]() и
не
компланарны, так как вектор
не
лежит в плоскости ACD.
и
не
компланарны, так как вектор
не
лежит в плоскости ACD.
Найдём квадрат длины вектора. Он равен сумме квадратов его координат. То есть необходимо возвести в квадрат каждую координату и полученные результаты сложить.
Найдём непосредственно длину вектора. Она равна квадратному корню из суммы координат вектора. Вновь полученное число и будет являться длиной исходного
Направляющие косинусы вектора |
|||||||||||||||||||||||||||||||||||||||||||||||||
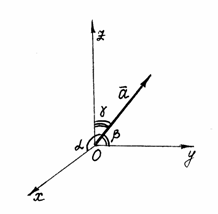
Направление
вектора в пространстве определяется
углами
Рис. 12
Из
свойств проекций:
Легко показать, что
1)
2) координаты
любого единичного вектора совпадают
с его направляющими косинусами: |
|||||||||||||||||||||||||||||||||||||||||||||||||
§ 6. Деление отрезка в данном отношении |
|||||||||||||||||||||||||||||||||||||||||||||||||
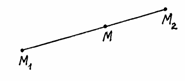
Говорят,
что точка
Рис. 13
Пусть
координаты точек
В
частности, если
–
середина отрезка
,
то
Пример
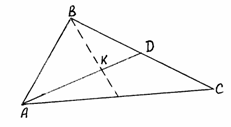
4. Даны вершины
треугольника
Решение. AD –
медиана, следовательно, D –
середина
отрезка BC,
ее координаты находятся по формулам
(2.7):
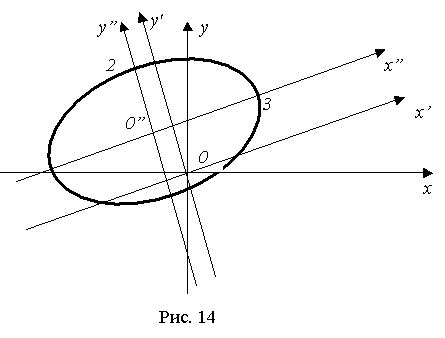
Рис. 14
Пример
5. Показать, что
точки
Решение.
Рассмотрим векторы
Рис. 15 15 Действия над векторами, заданными проекциями Пусть векторы а=(ax; ay; az) и b=( bx; by; bz) заданы своими проекциями на оси координат Ox,Oy,Oz или, что то же самое а = ах •i + ау • j +аz • k, b =bх • i + bу • j + bz • k. Линейные операции над векторами Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать: 1. а ± b = (ах±bх)i + (ау±by)j + ( az± bz)k, или кратко а ± b = (ах ±bx; ay± by; az ± bz). To есть при сложении (вычитании) векторових одноименные координаты складываются (вычитаются). 2. а = ах • i + ау • j + az • k или короче а = (ах; ау; аz). То есть при умножении вектора на скаляр координаты вектораумножаются на этот скаляр. Равенство векторов Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора а и b равны тогда и только тогда, когда выполняются равенства: aх= bх; ау=by; az= bz ,т. е.
Коллинеарность векторов Выясним условия коллинеарности векторов а и b, заданных своими координатами. Так как а || b, то можно записать а = • b, где -некоторое число. То есть
Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны. Координаты точки Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Для любой точки М координаты вектора ОМназываютсякоординатами точки М. ВекторОМназывается радиус-вектором точки М, обозначается r , т. е. ОМ= r . Следовательно, координаты точки — это координаты ее радиус-вектора
Координаты точки М записываются в виде М(х; у; z ). Координаты вектораНайдем координаты вектора а = АВ, если известны координаты точек A( x1; y1; z1) и В( x2;у2; z2). Имеем (см. рис. 13):
http://mathserfer.com/math/task.php?tname=vect_project - онлайн нахождение проекции вектора на вектор 16
17
18 Угол между векторами. Угол между вектором и осью. Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
рис.1. Обозначение.
Мы полагаем очевидным, что при параллельном переносе любого из двух векторов угол между ними остается неизменным, только в этом случае поворот одного из векторов осуществляется либо в общей для обоих векторов плоскости, либо в плоскости параллельной другому вектору. Введем понятие угла между вектором и осью. Определение. Углом между вектором и осью называется угол между данным вектором и любым правоориентированным вектором этой оси.
рис.2. Обозначение.
19
20
Теория Существует несколько вариантнов определения компланарности трех векторов в пространстве. Приведем основные из них. Три вектора называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскоти. Три вектора называются компланарными, если они лежат на параллельных плоскостях или на одной плоскости. Три вектора называются компланарными, если имеются равные им вектора, параллельные одной плоскости. Для трех векторов верны следующие утверждения:
Смешанное произведение трех векторов a=(xa,ya,za), b=(xb,yb,zb) и c=(xc,yc,zc) вычисляется по следующей формуле:
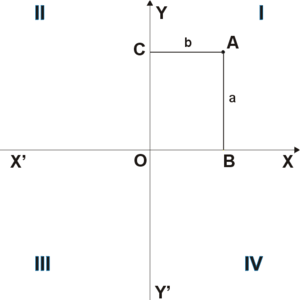
Если это произведение равно 0, то векторы компланарны 21 Прямоугольная система координат на плоскости Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси OY вверх, ось OX смотрела направо. Четыре угла (I, II, III, IV), образованные осями координат X'X и Y'Y, называются координатными углами или квадрантами (см. рис. 1).
Рис. 1 Положение
точки A
на плоскости определяется двумя
координатами x
и y.
Координата x
равна длине отрезка OB,
координата y —
длине отрезка OC
в выбранных единицах измерения. Отрезки
OB
и OC
определяются линиями, проведёнными
из точки A
параллельно осям Y'Y
и X'X
соответственно. Координата x
называется абсциссой
точки A,
координата y —
ординатой
точки A.
Записывают так:
Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату. [править] Прямоугольная система координат в пространстве Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений. Полярная
система координат задаётся лучом,
который называют нулевым или полярной
осью. Точка, из которой выходит этот
луч называется началом координат или
полюсом. Любая точка на плоскости
определяется двумя полярными
координатами: радиальной и угловой.
Радиальная координата (обычно
обозначается r)
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом или
азимутом
и обозначается
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке. Связь между декартовыми и полярными координатами Пару полярных координат r и можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса: x = rcos φ, y = rsin φ, в то время как две декартовы координаты x и y могут быть переведены в полярную координату r: r2 = y2 + x2 (по теореме Пифагора). Для определения угловой координаты следует принять во внимание два следующие соображения:
Для вычисления в интервале , можно воспользоваться такими уравнениями (arctg обозначает обратную функцию к тангенсу):
Для вычисления в интервале , можно воспользоваться такими уравнениями:[14]
Учитывая, что для вычисления полярного угла не достаточно знать отношение y к x, а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты x. 22
23 В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую. Уравнение вида
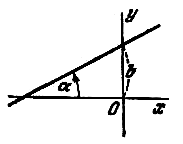
называется общим уравнением прямой. Угол
Уравнение
Если прямая задана общим уравнением , то ее угловой коэффициент определяется по формуле
Уравнение
Если
прямая проходит через точки
Уравнение
является уравнением прямой, проходящей через две точки ( , ) и ( , ). Если
известны угловые коэффициенты
Признаком параллельности двух прямых является равенство их угловых коэффициентов:
Признаком перпендикулярности двух прямых является соотношение
Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку. 24 1. Уравнение прямой, проходящей через данную точку A(x1, y1) в данном направлении, определяемом угловым коэффициентом k, y - y1 = k(x - x1). (1) Это уравнение определяет пучок прямых, проходящих через точку A(x1, y1), которая называется центром пучка. 2. Уравнение прямой, проходящей через две точки: A(x1, y1) и B(x2, y2), записывается так:
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле
25 3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом y = k1x + B1, y = k2x + B2, (4)
то угол между
ними
Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой. Если уравнения прямой заданы в общем виде A1x + B1y + C1 = 0, A2x + B2y + C2 = 0, (6) угол между ними определяется по формуле
4. Условия параллельности двух прямых: а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k1 = k2. (8) б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
5. Условия перпендикулярности двух прямых: а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
Это условие может быть записано также в виде k1k2 = -1. (11) б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства A1A2 + B1B2 = 0. (12)
26 Уравнение прямой в отрезках Если в общем уравнении прямой Ах + Ву + С = 0 С 0, то, разделив на –С, получим: или , где Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках. С = 1, , а = -1, b = 1. Векторно-параметрическое уравнение прямой
где
В координатах (параметрические уравнения):
2 Одна или две координаты направляющего вектора прямой
могут быть равны нулю, это означает, что числитель соответствующей дроби тоже равен нулю. Если в (1) ввести параметр t
то уравнения прямой можно записать в виде
Эти уравнения называются параметрическими уравнениями прямой. Они имеют механический смысл: если параметр t рассматривать как время, а x, y, z — как координаты материальной точки, то параметрические уравнения описывают равномерное прямолинейное движение точки со скоростью
= {l, m, n} , (x0, y0, z0) —начальное положение точки (при t = 0 ). 27 Расстояние от точки до прямой Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1: (1) Координаты x1 и у1 могут быть найдены как решение системы уравнений: Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0, то, решая, получим: Подставляя эти выражения в уравнение (1), находим: .
Теорема доказана.
Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1. k1 = -3; k2 = 2 tg = ; = /4.
Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны. Находим: k1 = 3/5, k2 = -5/3, k1k2 = -1, следовательно, прямые перпендикулярны.
Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С. Находим уравнение стороны АВ: ; 4x = 6y – 6; 2x – 3y + 3 = 0; Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b. k = . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: . Ответ: 3x + 2y – 34 = 0. Найти расстояние от начала координат до прямой x + y - 2 = 0.
Решение. Приведем уравнение прямой к нормальному виду. Нормирующий множитель
В нормальном виде уравнение прямой запишется так:
Свободный член
в нормальном уравнении прямой, взятый
по абсолютной величине, дает искомое
расстояние
28
29
30
31 Приведение уравнений кривых второго порядка к каноническому виду
32 Нормальным уравнением плоскости называется ее уравнение, написанное в виде
где
Пусть
Если
точка
имеет
координаты
, то отклонение точки от этой плоскости дается формулой
Очевидно,
Общее уравнение плоскости
приводится к нормальному виду (1) умножением на нормирущий множитель, определяемый формулой
знак нормирующего множителя берется противоположным знаку свободного члена нормируемого уравнения. 33 Нормальное уравнение плоскости
где
Приведение общего уравнения плоскости к нормальному виду:
Здесь
34
35 Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости
Пусть
заданы точки М1(x1,
y1,
z1),
M2(x2,
y2,
z2)
и вектор
Составим
уравнение плоскости, проходящей через
данные точки М1
и М2
и произвольную точку М(х, у, z)
параллельно вектору
Векторы
(
Уравнение
плоскости: 36
Уравнение плоскости, проходящей через три заданные точки Пусть даны три точки M0(x0 , y0, z0), M1(x1, y1, z1), M2(x2, y2, z2), которые лежат в одной плоскости. Пусть М (x, y, z) произвольная точка этой плоскости. Тогда векторы M0M, M0M1, M0M2 лежат в одной плоскости и их смешанное произведение равно нулю: M0M×(M0M1·M0M2) = 0 Расписывая смешанные произведения в координатной форме, получим:
Раскроем определитель по первой строке:
Если ввести
обозначения
37 Уравнение плоскости в отрезках. Полное уравнение может быть приведено к виду
Это уравнение в отрезках. Числа а,b,с имеют простой геометрический смысл - они равны величинам отрезков, которые отсекаются на осях 0х, 0у, 0z.
38 УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Р
Под углом
между двумя плоскостями будем понимать
один из двугранных углов, образованных
этими плоскостями. Очевидно, что угол
между нормальными векторами
Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.
Условие параллельности двух плоскостей.
Две плоскости α1
и α2 параллельны тогда и только
тогда, когда их нормальные векторы
и
параллельны,
а значит
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
Условие перпендикулярности плоскостей.
Ясно, что две
плоскости перпендикулярны тогда и
только тогда, когда их нормальные
векторы перпендикулярны, а следовательно,
Таким образом,
Примеры.
M(-2; 1; 4) параллельно плоскости 3x+2y-7z+8=0.
Уравнение плоскости
будем искать в виде Ax+By+Cz+D=0.
Из условия параллельности плоскостей
следует, что:
Кроме того, так какM α, то-6+2-28+D=0, D=32. Итак, искомое уравнение 3x+2y-7z+32=0.
Так как M1 α, то используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x-1)+B(y-1)+C(z-1)=0. Далее, так как M2 α, то подставив координары точки в выписанное уравнение, получим равенство -A-2C=0 или A+2C=0. Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C=0. Выразим коэффициенты Aи Bчерез C: A=-2C, B=C и подставим их в исходное уравнение: -2C(x-1)+C(y-1)+C(z-1)=0. Окончательно получаем -2x+y+z=0.
Так как M α, то A(x+2)+B(x-3)+C(z-6)=0.
По условию задачи
Итак уравнение плоскости принимает вид 13(x+2)-8(y-3)+z-6=0 или 13x-8y+z+44=0. 40 Каноническое уравнение прямой в пространстве
Пусть
прямая проходит через точку M1
(x1, y1,
z1) и параллельна
вектору
Возьмем произвольную точку M (x, y, z) на этой прямой и найдем зависимость между x, y, z. Построим вектор
Векторы
41 Уравнение прямой в пространстве, проходящей через две точки Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) и M2(x2, y2, z2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
Кроме того, для точки М1 можно записать:
Решая совместно эти уравнения, получим:
Это уравнение прямой, проходящей через две точки в пространстве. 42 Параметрическое уравнение прямой
Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.
Пусть в координатном
пространстве
а) точка
б) ненулевой
вектор
Требуется составить
уравнение прямой, коллинеарной вектору
Выберем на прямой
произвольную точку
Точка
где
—
направляющий вектор прямой, а
Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве
(4.33)
где
43 Угол между двумя прямыми Буду кратким. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x1; y1; z1) и b = (x2; y2; z2), то сможете найти угол. Точнее, косинус угла по формуле:
44 Условия параллельности и перпендикулярности прямых в пространстве Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.
45 - 46
47 Логическое высказывание — упрощение термина «Суждение» из формальной логики, используется в математической логике. Высказыванием является повествовательное предложение, которое формализует некоторое выражение мысли. Это утверждение, которому всегда можно поставить в соответствие одно из двух логических значений: ложь (0, ложно, false) или истина (1, истинно, true). Логическое высказывание принято обозначать заглавными латинскими буквами. Высказывательной формой называется логическое высказывание, в котором один из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание. Пример: A(x) = «В городе x идет дождь.» A — высказывательная форма, x — объект. Высказывание обычно имеет только одно логическое значение. Так, например, «Париж — столица Франции» — высказывание, а предложение «На улице идет дождь» высказыванием не является. Аналогично, «5>3» — высказывание, а выражение «2+3» — нет. Как правило, высказывания обозначают маленькими латинскими буквами. Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот. Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны. Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно. Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно. Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны. Кванторное
логическое высказывание с квантором
всеобщности
( Кванторное
логическое высказывание с квантором
существования ( 48
49 ПОВЕРХНОСТЬ ВТОРОГО ПОРЯДКА множество точек 3-мерного действительного (или комплексноро) пространства, координаты к-рых в декартовой системе удовлетворяют алгебраич. уравнению 2-й степени
Уравнение (*) может и не определять действительного геометрич. образа, в таких случаях говорят, что уравнение (*) определяет мнимую П. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат на нек-рый угол к одному из 17 приведенных ниже канонич. видов, каждому из к-рых соответствует определенный класс поверхностей. Именно, невырождающиеся нераспадающиеся поверхности:
вырождающиеся нераспадающиеся поверхности: цилиндрические поверхности, -
конические поверхности -
вырождающиеся распадающиеся поверхности:
х 2 + а 2=0 -пара мнимых параллельных плоскостей. x2= 0 -пара совпадающих плоскостей. П. в. п., имеющие единственный центр симметрии (центр П. в. п.), наз. центральными поверхностями. Координаты центра определяются решением системы:
П. в. п. без центра симметрии или с неопределенным центром наз. нецентральными поверхностями. Исследование П. в. п. может быть осуществлено без приведения общего уравнения к канонич. виду. Это достигается совместным рассмотрением значений т. н. основных инвариантов П. в. п.- выражений, составленных из коэффициентов уравнения (*), значения к-рых не меняются при параллельном переносе и повороте системы координат:
и семиинвариантов (полуинвариантов) D' и D", к-рые являются инвариантами относительно поворота системы координат: D' = D11 + D22 + D33, где Dij - алгебраич. дополнение элемента а ik, в D;
50 Эллипсоид Определение
13 . 3 Эллипсоидом называется
поверхность, каноническое уравнение
которой имеет вид
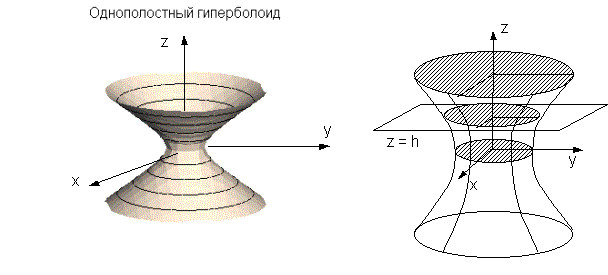
51 52 Однополостный гиперболоид Каноническое уравнение однополостного гиперболоида имеет вид
Координатные плоскости являются плоскостями симметрии, так как при замене х на − х, у на − у, z на − z уравнение не меняется.
Если
рассечь поверхность плоскостями z
= h, получим
кривые с уравнениями
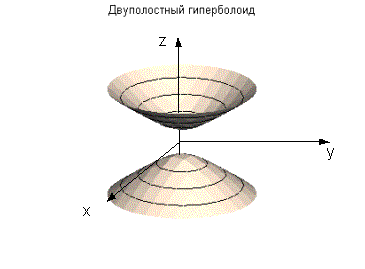
Точки этих гипербол являются вершинами эллипсов, получаемых при сечении поверхности плоскостями z = h. 53 Двуполостный гиперболоид Каноническое уравнение вуполостного гиперболоида имеет вид
Координатные
плоскости являются плоскостями
симметрии: при замене х
на − х,
у
на − у,
z
на − z
уравнение не меняется.
Если
рассечь поверхность плоскостями z
= h ( | z
| ≥ c
), получим эллипсы с уравнениями
При
| h
| ≥ с
получаются вещественные эллипсы с
полуосями
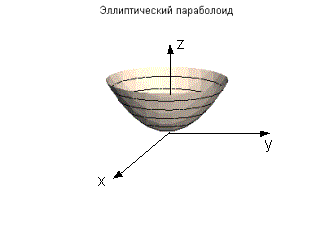
Точки этих гипербол являются вершинами эллипсов, получаемых при сечении поверхности плоскостями z = h (| h | ≥ с). 54 Эллиптический параболоид Каноническое уравнение эллиптического параболоида имеет вид
Координатные плоскости Оyz и OXZ являются плоскостями симметрии: при замене х на - х, у на - у уравнение не меняется. Поверхность проходит через начало координат и расположена над плоскостью Оху, так как z ≥ 0.
При сечениях z = h получаются эллипсы
полуоси
которых
55
Конус второго порядка Конусом второго порядка называется поверхность, заданная относительно специально выбранной системы координат уравнением x2/a2+y2/b2-z2/c2=0 (1). Из уравнения конуса второго порядка следует, что, если точка с координатами (x, y, z) лежит на этой поверхности, то на этой поверхности лежит и точка (±x, ±y, ±z) при любом наборе знаков + и -. Следовательно, координатные плоскости являются плоскостями симметрии конуса второго порядка. Будем считать, что a≥b. 1) Если a=b, то конус второго порядка называется конусом вращения и получается вращением вокруг оси oz двух пересекающихся прямых y/b-z/c=0 и y/b+z/c=0. 2) Пусть a>b. Начало координат называют вершиной конуса второго порядка. Ось oz — осью симметрии конуса. Основное свойство конуса: если точка M0(x0, y0, z0) лежит на конусе второго порядка, то и вся прямая OM0 также лежит на нем, где O - вершина конуса, точка M0 отлична от вершины конуса. Конус
второго порядка, заданный уравнением
(1) определяет собой поверхность,
образованную следующим образом: каждая
точка эллипса x2/(ac/h)2+y2/(bc/h)2=1
соединяется с началом координат по
прямым.
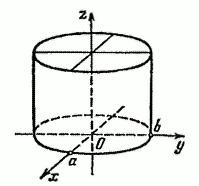
56 Цилиндры второго порядка а) Эллиптический цилиндр
Уравнение
(14) не содержит переменной
в плоскости . Эллипс (14) называют направляющей линией данной поверхности, а все возможные положения указанной движущейся прямой – образующими. Вообще
поверхность, описываемая прямой,
остающейся параллельной некоторому
заданному направлению и пересекающей
данную линию
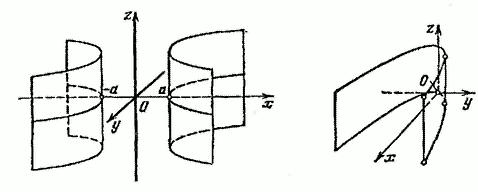
Рис.49 б) Гиперболический и параболический цилиндры
В данном случае направляющими линиями поверхностей являются гипербола и парабола, а образующими - прямые параллельные оси и проходящие через гиперболу или параболу в плоскости . Поверхности (15) и (16) изображены на рис. 50 и 51. в) Параллельные и пересекающиеся плоскости. Прямая.
Для поверхности (17) направляющими являются прямые линии
Поэтому
поверхность (17) есть пара пересекающихся
плоскостей. В уравнении поверхностей
(18) и (19) отсутствуют по две координаты.
Уравнение (18) в плоскости
есть
пара прямых
Рис. 50 Рис. 51 Если
мы будем брать
и
любые
Уравнение
(19) описывает плоскость
,
так как этому уравнению удовлетворяют
любые точки вида
Можно
также рассматривать
Уравнению
(20) удовлетворяет любая точка с
57 Определение множества Математическим анализом называется раздел математики, занимающийся исследованием функций на основе идеи бесконечно малой функции. Основными понятиями математического анализа являются величина, множество, функция, бесконечно малая функция, предел, производная, интеграл. Величиной называется все что может быть измерено и выражено числом. Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п. Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки. Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится). Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства. Например, перечислением заданы следующие множества:
Множество (-∞;+∞) называется числовой прямой, а любое число — точкой этой прямой. Пусть a — произвольная точка числовой прямой иδ — положительное число. Интервал (a-δ; a+δ) называется δ-окрестностью точки а. Множество Х ограничено сверху (снизу), если существует такое число c, что для любого x ∈ X выполняется неравенство x≤с (x≥c). Число с в этом случае называется верхней(нижней) гранью множества Х. Множество, ограниченное и сверху и снизу, называется ограниченным. Наименьшая (наибольшая) из верхних (нижних) граней множества называется точной верхней (нижней) гранью этого множества. Основные числовые множества
Обозначения Множество
вещественных чисел обозначается
Определения Ограниченное сверху множество Определение
Множество
Верхняя граница множества Определение Верхней границей множества называется любое число такое, что для любого из множества , Ограниченное снизу множество Определение
Множество
является
ограниченным снизу если существует
число
такое,
что для любого
из
множества
,
Нижняя граница множества Определение Нижней границей множества называется любое число такое, что для любого из множества , Несобственные числа Определение
Несобственное число
Несобственное
число
Считаем,
что
Точные границы Определение
Точная верхняя граница множества
это
его наименьшая верхняя
граница.
Точная верхняя граница обозначается
Определение
Точная нижняя граница множества
это
его наибольшая нижняя
граница
Точная нижняя граница обозначается
58 вещественное число, - положительное число, отрицательное число или нуль. Понятие Д. ч. возникло путем расширения понятия рационального числа. Необходимость этого расширения обусловлена как практическим использованием математики при выражении значения любой величины с помощью вполне определенного числа, так и внутренним развитием самой математики, в частности стремлением расширить область применимости ряда операций над числами (извлечение корня, вычисление логарифмов, решение уравнений и т. п.). К общему понятию Д. ч. подошли еще древнегреческие математики в своей теории несоизмеримых отрезков, однако как самостоятельное понятие оно было сформулировано впервые лишь в 17 в. И. Ньютоном (I. Newton) в "Arithmetica Universales": "Число есть не столько совокупность нескольких единиц, сколько отвлеченное отношение какой-нибудь величины к другой, однородной с ней принятой за единицу". Строгие теории Д. ч. были построены в конце 19 в. Г. Кантором (G. Cantor), P. Дедекиндом (R. Dedekind) и К. Вейерштрассом (К. Weierstrass). Действительные числа образуют совокупность элементов, обладающую следующими свойствами. I. Свойство упорядоченности. Для любых двух чисел а и 6 определено соотношение порядка, т. е. два любых Д. ч. аи bудовлетворяют одному и только одному из следующих соотношений: а<b, а=b или а>b; при этом, если а<bи b<с, то а<с (транзитивность упорядоченности). II. Свойство oпepaции сложения. Для любой упорядоченной пары чисел аи bопределено такое единственное число, наз. их суммой и обозначаемое через а+b, что выполняются следующие свойства: II1 )а+b=b+а (коммутативность); II2) a+(b+с)=(а+b)+с для любых чисел а, b и с(ассоциативность); II3) существует такое число, наз. нулем и обозначаемое 0, что а+0=а для любого числа а; II4) для любого числа асуществует такое число, наз. противоположным а и обозначаемое через -а, что а+ (-a) = 0; II5) если а<b, то а+с<b+с для любого числа с. Нуль единствен, и для каждого числа единственно противоположное ему число. Для любой упорядоченной пары чисел а и bчисло а+ (-b)наз. разностью чисел а и bи обозначается а-b. III. Свойство операции умножения. Для любой упорядоченной пары чисел аи bопределено такое единственное число, наз. их произведением и обозначаемое через аb, что: III1) ab=ba (коммутативность); III2) a(bc)=(ab)cдля любых чисел a, bи с (ассоциативность); III3) существует такое число, наз. единицей и обозначаемое через 1, что a1=a для любого числа а; III4) для любого числа а, не равного нулю, существует такое число, наз. обратным данному и обозначаемое через 1/a, что а(1/а)=1; III5) если а<b и с>0, то ac<bc. Эти свойства гарантируют единственность единицы и единственность обратного каждому элементу. Для любой упорядоченной пары чисел аи b, b неравно 0, число a(1/b )наз. частным от деления а на 6 и обозначается a/b. Число
1+1 обозначается 2, число 2+1 обозначается
3 и т. д. Эти числа 1, 2, 3... наз. натуральными
числами. Числа, большие нуля, наз.
положительными, а числа, меньшие нуля,-
отрицательными. Числа
IV. Свойство дистрибутивности умножения относительно сложения. Для любой тройки чисел а, bи с( а+b) с=ас+bс. Совокупность элементов, удовлетворяющих всем перечисленным свойствам, образует линейно упорядоченное поле. Д. ч. обладают еще двумя важными, свойствами. V. Архимедово свойство. Каково бы ни было число а, существует такое целое число п, что n>а. Совокупность элементов, удовлетворяющих свойствам I - V, образует упорядоченное архимедово поле. Таковым является не только совокупность Д. ч., но и множество рациональных чисел. Существенным свойством Д. ч. является свойство их непрерывности, к-рым рациональные числа не обладают. VI. Свойство непрерывности. Для всякой системы вложенных отрезков
существует
хотя бы одно число, к-рое принадлежит
всем отрезкам данной системы. Это
свойство наз. также принципом вложенных
отрезков Кантора. Если длины b
п- а п вложенных
отрезков стремятся к нулю при
то
Отсюда следует, что множество Д. ч. (в отличие, напр., от множества рациональных чисел) невозможно расширить с сохранением свойств I - V, т. е. не существует множества, в к-ром было бы введено соотношение порядка, операции сложения и умножения, удовлетворяющие свойствам I - V, и к-рое содержало бы подмножество, изоморфное множеству Д. ч., и не совпадало бы с ним. Д. ч. существенно больше, чем рациональных чисел, именно рациональные числа составляют счетное подмножество множества Д. ч., которое само несчетно. Как рациональные, так и иррациональные числа обладают свойством плотности во множестве всех Д. ч.: каковы бы ни были два Д. ч. а и b, а<b, найдутся такое рациональное r, что а<r<b, и такое иррациональное x, что a<x<b. Со
свойством непрерывности Д. ч. тесно
связано свойство их полноты, состоящее
в том, что всякая фундаментальная
последовательность Д. ч. является
сходящейся. Следует отметить, что
множество одних только рациональных
чисел уже не обладает свойством
полноты: в нем существуют фундаментальные
последовательности, не сходящиеся ни
к какому рациональному числу. Свойство
непрерывности множества Д. ч. (их
полнота) связано с их применением для
измерения тех или иных непрерывных
величин, например для измерения длин
геометрических отрезков: если выбрать
отрезок единичной длины, то в силу
непрерывности множества Д. ч. каждому
отрезку сопоставляется определенное
положительное Д. ч.- его длина. Образно
говоря, непрерывность множества Д. ч.
означает, что в нем нет "пустых
мест". Из непрерывности множества
Д. ч. следует, что из всякого положительного
числа можно извлечь корень я-и степени
(п- натуральное число) и что всякое
положительное число имеет логарифм
по любому основанию а>0, Свойство непрерывности Д. ч. можно сформулировать иначе. VI'. Всякое ограниченное сверху множество имеет точную верхнюю грань (см. Верхняя и нижняя грани). Можно
использовать также понятие сечения
АВ
в области Д. <ч. (см. Дедекиндово
сечение).
Говорят, что сечение АВ
производится числом а, если
Всякое число производит сечение. Свойство непрерывности, наз. непрерывностью Д. ч. по Дедекинду, состоит в справедливости обратного утверждения. VI". Всякое сечение Д. ч. производится нек-рым числом. Такое число единственно и является либо наибольшим в нижнем классе, либо наименьшим в верхнем. Каждое из утверждений VI, VI' и VI" равносильно каждому из остальных в том смысле, что из каждого из них, принятого за аксиому (и остальных свойств I-V), вытекают два других. Более того, как из свойства VI', так и из свойства VI" (и свойств I - IV) вытекает не только VI, но и архимедово свойство V. Определение Д. ч. как совокупности элементов, обладающих свойствами I-VI, является аксиоматич. построением теории Д. ч. Существует несколько методов построения этой теории на основе рациональных чисел. Первая такая теория была построена Р. Дедекиндом на основе понятия сечения R1|R2 в области рациональных чисел. Если для данного сечения R1|R2 рациональных чисел в Rr есть наибольшее рациональное число или в R2 наименьшее, то говорят, что сечение R1|R2 производится этим числом. Всякое рациональное число производит сечение. Сечение, у к-рого в нижнем классе нет наибольшего, а в верхнем нет наименьшего, наз. иррациональным числом. Рациональные и иррациональные числа наз. действительным и числами, при этом для единообразия рациональные числа рассматриваются как сечения, к-рые они производят. Пусть
x=R1|R2 и x'
= R'1|R'2.
Д. ч. хназ. меньшим Д. ч. х' (или, что
то же самое, х' наз. большим х),
если
Сумма и произведение Д. ч. всегда существуют, единственны и вся совокупность таким образом определенных Д. ч. с введенным в них отношением порядка и операциями сложения и умножения обладает свойствами I - VI. Абсолютная величина (модуль) действительного числа
Определение.
Абсолютной
величиной (модулем) действительного
числа
Так, например,
Свойства модуля
Если
Кроме того, справедливо соотношение:
В то же время справедливы неравенства:
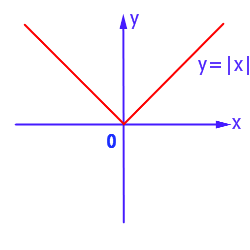
График функции
График функции имеет следующий вид:
Простейшее уравнение с модулем Рассмотрим простейшее уравнение с модулем, имеющее вид:
Поскольку
то данное уравнение эквивалентно совокупности двух систем:
Для решения исходного уравнения остается лишь решить две этих системы и объединить полученные ответы.
59
60 Определение Пусть
множество X
— это либо множество вещественных
чисел
Примеры
Свойства
|
61


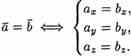
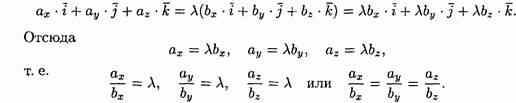
 AB=OB-OA=(x2i+y2j+z2k)-(x1i+y1j+z1k)=(x2 -
x1)i+(y2 -
y1)j+(z2 -
z1)k
AB=OB-OA=(x2i+y2j+z2k)-(x1i+y1j+z1k)=(x2 -
x1)i+(y2 -
y1)j+(z2 -
z1)k









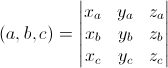

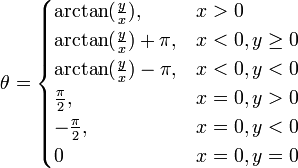










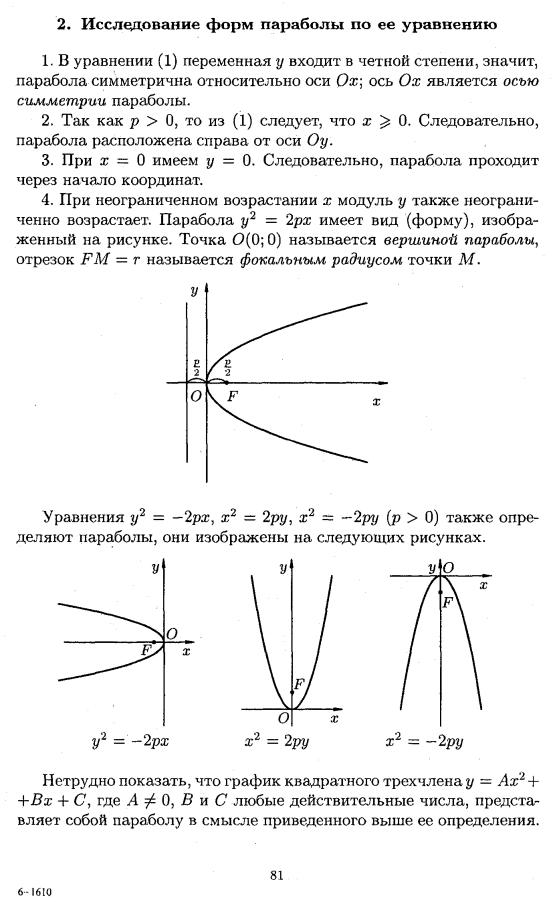
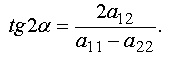


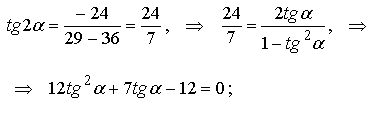
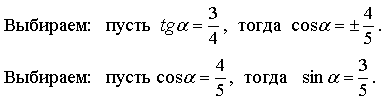
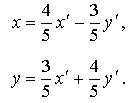
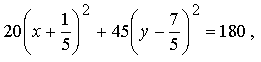

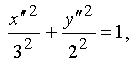
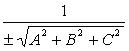 -
нормирующий множитель плоскости, знак
которого выбирается противоположным
знаку D, если
-
нормирующий множитель плоскости, знак
которого выбирается противоположным
знаку D, если
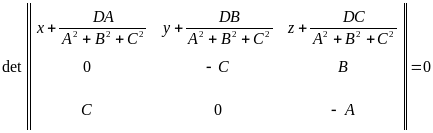 ,
,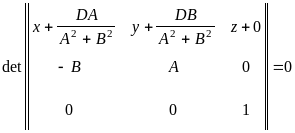 .
.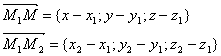 и
вектор
должны
быть компланарны, т.е.
и
вектор
должны
быть компланарны, т.е.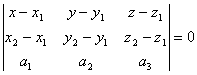
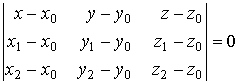
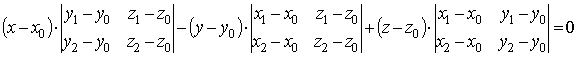
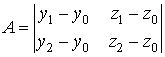 ,
,
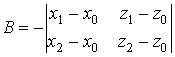 ,
,
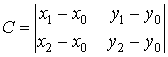 ,
то получим A·(x
- x0)
+ B·(y - y0)
+ C·(z - z0)
= 0, уравнение плоскости.
,
то получим A·(x
- x0)
+ B·(y - y0)
+ C·(z - z0)
= 0, уравнение плоскости.
 ассмотрим
две плоскости α1 и α2,
заданные соответственно уравнениями:
ассмотрим
две плоскости α1 и α2,
заданные соответственно уравнениями: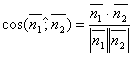 .
Т.к.
.
Т.к. .
.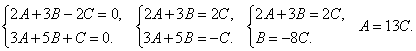

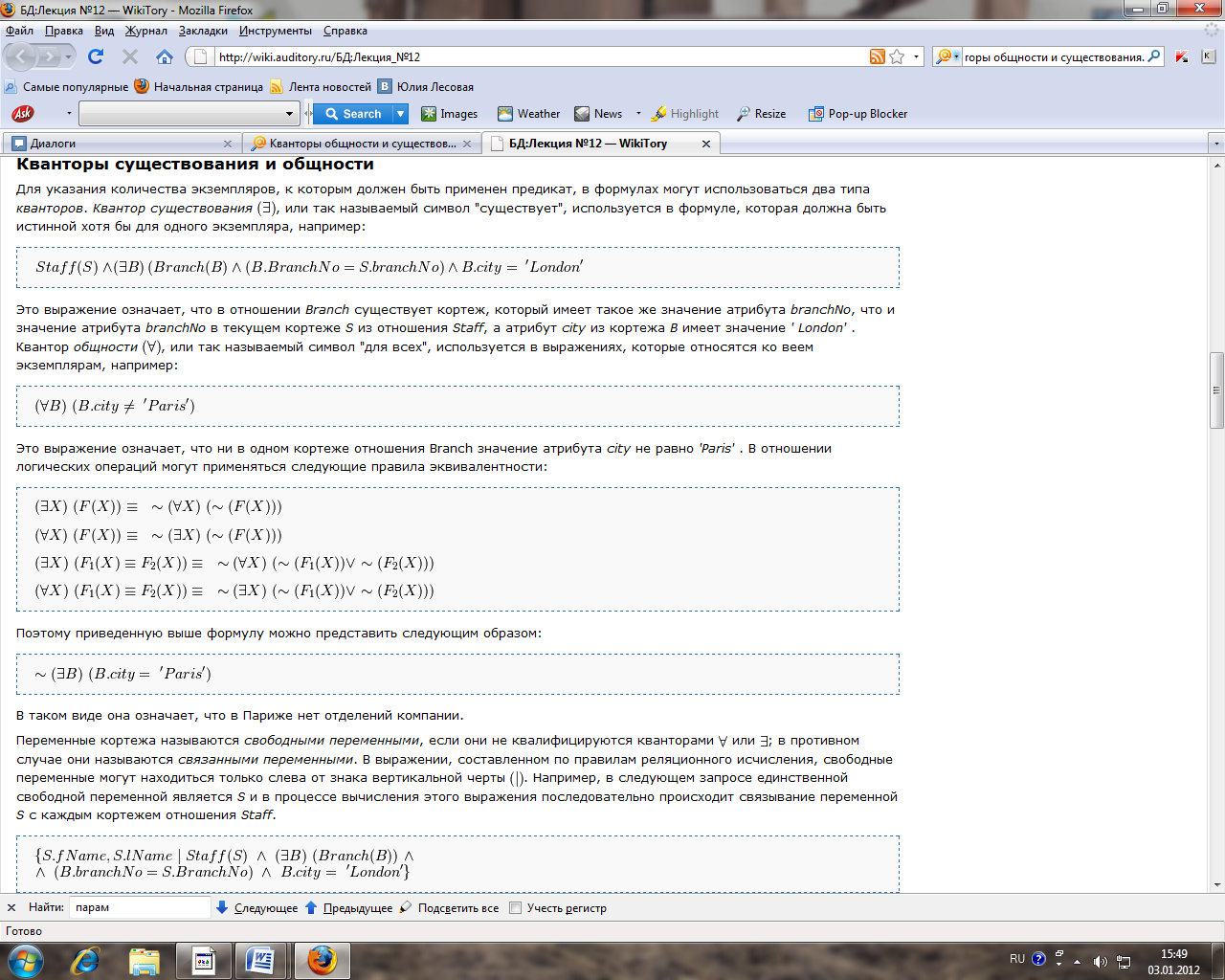
 (*)
(*)
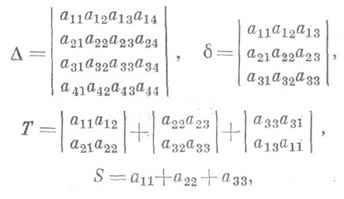

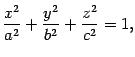 (
13 .3) где
(
13 .3) где
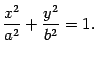 (
13 .4) По теореме 12.2 получаем, что линия
пересечения является эллипсом с
полуосями
и
(рис.
13.3).
(
13 .4) По теореме 12.2 получаем, что линия
пересечения является эллипсом с
полуосями
и
(рис.
13.3).
 Рис.
13 . 3 .Сечение плоскостью
Аналогично,
сечение в плоскости
Рис.
13 . 3 .Сечение плоскостью
Аналогично,
сечение в плоскости
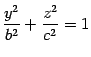 с
полуосями
и
,
а сечение плоскостью
с
полуосями
и
,
а сечение плоскостью
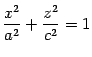 с
полуосями
и
(рис.
13.4)
с
полуосями
и
(рис.
13.4)
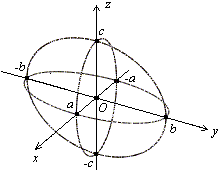 Рис.
13 . 4 .Сечения эллипсоида координатными
плоскостями Нарисованный "каркас"
из сечений уже дает представление об
эллипсоиде. Но чтобы выяснить, как
ведет себя поверхность между
нарисованными кривыми, рассмотрим
сечение эллипсоида плоскостью
Рис.
13 . 4 .Сечения эллипсоида координатными
плоскостями Нарисованный "каркас"
из сечений уже дает представление об
эллипсоиде. Но чтобы выяснить, как
ведет себя поверхность между
нарисованными кривыми, рассмотрим
сечение эллипсоида плоскостью
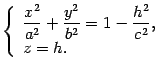 Очевидно,
что если
Очевидно,
что если
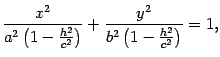 то
есть к виду
то
есть к виду
 (
13 .5) где
(
13 .5) где
 ,
,
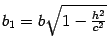 .
Уравнение ( 13.5 ) является уравнением
эллипса, подобного эллипсу, задаваемому
уравнением ( 13.4 ), с коэффициентом
подобия
.
Уравнение ( 13.5 ) является уравнением
эллипса, подобного эллипсу, задаваемому
уравнением ( 13.4 ), с коэффициентом
подобия
 и
полуосями
и
полуосями
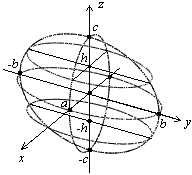 Рис.
13 . 5 .Дополнительные сечения эллипсоида
Таким образом, весь эллипсоид составлен
из эллипсов, лежащих в плоскостях,
параллельных плоскости
и
подобных эллипсу в плоскости
.
Рисунок 13.6 дает более привычное глазу
изображение эллипсоида.
Рис.
13 . 5 .Дополнительные сечения эллипсоида
Таким образом, весь эллипсоид составлен
из эллипсов, лежащих в плоскостях,
параллельных плоскости
и
подобных эллипсу в плоскости
.
Рисунок 13.6 дает более привычное глазу
изображение эллипсоида.
 Рис.
13 . 6 .Эллипсоид Так же, как для эллипса,
точки пересечения эллипсоида с
координатными осями называются
вершинами эллипсоида, центр симметрии --
центром эллипсоида. Числа
,
,
называются
полуосями. Если полуоси попарно
различны, то эллипсоид называется
трехосным . Если две полуоси равны
друг другу, то эллипсоид называется
эллипсоидом вращения . Эллипсоид
вращения может быть получен вращением
эллипса вокруг одной из осей. Например,
если
Рис.
13 . 6 .Эллипсоид Так же, как для эллипса,
точки пересечения эллипсоида с
координатными осями называются
вершинами эллипсоида, центр симметрии --
центром эллипсоида. Числа
,
,
называются
полуосями. Если полуоси попарно
различны, то эллипсоид называется
трехосным . Если две полуоси равны
друг другу, то эллипсоид называется
эллипсоидом вращения . Эллипсоид
вращения может быть получен вращением
эллипса вокруг одной из осей. Например,
если
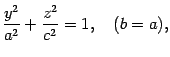 лежащего
в плоскости
,
при вращении его вокруг оси
(рис.
13.7).
лежащего
в плоскости
,
при вращении его вокруг оси
(рис.
13.7).
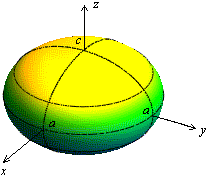 Рис.
13 . 7 .Эллипсоид вращения
Рис.
13 . 7 .Эллипсоид вращения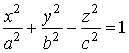 .
.
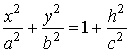 ,
z = h,
(- ∞ < h
< + ∞). Получили уравнение эллипса с
полуосями
,
z = h,
(- ∞ < h
< + ∞). Получили уравнение эллипса с
полуосями
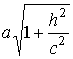 и
и
 .
При h
= 0 эллипс имеет наименьшие полуоси,
он носит название горлового. Когда |
h
| растёт, то полуоси эллипсов растут
вместе с h.
Сечения плоскостями х
= 0, у
= 0 представляют собой гиперболы
.
При h
= 0 эллипс имеет наименьшие полуоси,
он носит название горлового. Когда |
h
| растёт, то полуоси эллипсов растут
вместе с h.
Сечения плоскостями х
= 0, у
= 0 представляют собой гиперболы
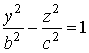 ,
,
 .
. .
.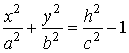 ,
z = h,
(- c
< h
< + c).
При - c < h
< + c имеем
мнимые эллипсы. Следовательно,
поверхность расположена ниже плоскости
z = − с
и выше плоскости z
= + с.
,
z = h,
(- c
< h
< + c).
При - c < h
< + c имеем
мнимые эллипсы. Следовательно,
поверхность расположена ниже плоскости
z = − с
и выше плоскости z
= + с.
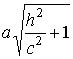 и
и
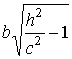 ,
которые растут с ростом | h
|. Сечения плоскостями х
= 0, у
= 0 представляют собой сопряжённые
гиперболы
,
которые растут с ростом | h
|. Сечения плоскостями х
= 0, у
= 0 представляют собой сопряжённые
гиперболы
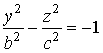 ,
,
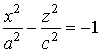 .
.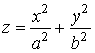 .
.
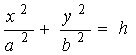 ,
,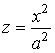 ,
,
 ,
точки которых являются вершинами
указанных выше эллипсов.
,
точки которых являются вершинами
указанных выше эллипсов.