15. Законы больших чисел и предельные теоремы. Теорема Бернулли. Теорема Чебышева. Центральная предельная теорема. Теорема Муавра – Лапласа.

Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений. Теоретическим обоснованием этого замечательного свойства случайных явлений является закон больших чисел.

Закон больших чисел.Если случайные величины x₁, x₂, …, x_n, … попарно независимы и ,то для любого e > 0

Теорема Бернулли. Пусть m n - число успехов в n испытаниях Бернулли и p - вероятность успеха в отдельном испытании. Тогда при любом e > 0 справедливо

Неравенство Чебышева. Если случайная величина x имеет дисперсию, то для любого e > 0 справедливо неравенство , где Mx и Dx - математическое ожидание и дисперсия случайной величины x

Центральная предельная теорема. Если случайные величины x₁, x₂, …, x_n, … попарно независимы, одинаково распределены и имеют конечную дисперсию, то при n → ∞ равномерно по x (-∞ , ∞)

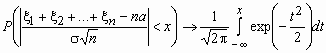
Теорема Муавра — Лапласа. Рассмотрим схему Бернулли с вероятностью успеха то есть пусть дана последовательность независимых случайных величин где

Определим как число успехов в первых n испытаниях:

Тогда:

то есть:

16. Асимптотическое распределение среднего арифметического независимых случайных величин и относительные частоты.