13.Способы расчета средних величин. Простые и взвешенные средние. Порядок применения взвешенных средних.
Степенные
средние в зависимости от представления
исходных данных могут быть простыми
и взвешенными.
Если
вариант
встречается
один раз, расчеты проводим по средней
простой (например зарплата в 3 тыс.руб.
встречается только у одного рабочего),
а если вариант повторяется неодинаковое
число раз, то есть имеет разные частоты
(например
зарплата в 4 тыс.рублей встречается у
пяти работников), то расчет проводим по
средней взвешенной.
Формула степенной простой в общем виде
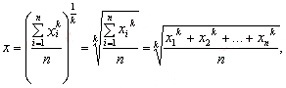
где:
—
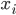индивидуальное
значение признака
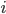-й
единицы совокупности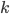
—
показатель
степени средней величины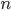
—
число
единиц совокупности
Формула степенной средней взвещенной в общем виде
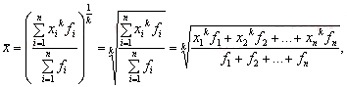
где:
—
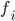частота
повторения
-й
варианты.
В зависимости от того, какое значение принимает показатель степени средней величины , получаем различные виды средних:
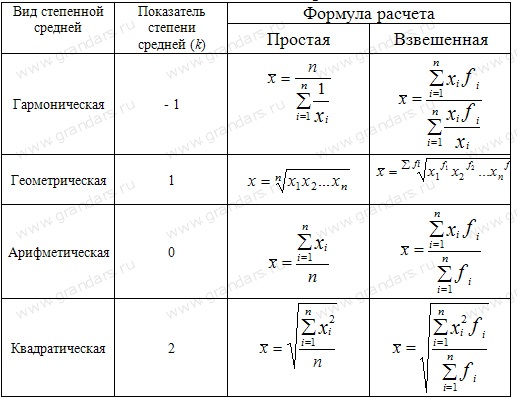
При расчете различных степенных средних по одним и тем же данным значения средних будут неодинаковыми. Чем выше показатель степени ( ), тем больше величина средней, т.е. действует правило мажорантности средних:
14.Вариация и задачи ее статистического изучения. Вариационный ряд: порядок его построения и графического изображения.
Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.
Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
ариационный
ряд
(set of order statistic) — последовательность
значений заданной выборки
,
расположенных в порядке неубывания:
k-й
порядковой статистикой
называется k-е
значение в вариационном ряду
.
Рангом
наблюдения
называется
его порядковый номер в вариационном
ряду:
.
Если
—
простая
выборка
и функция
распределения
случайной величины
непрерывна,
то с вероятностью 1 вариационный ряд не
содержит равных элементов (все неравенства
строгие), и данное выше определение
ранга корректно. Если же функция
распределения разрывна (в частности,
если случайная величина
дискретна),
то в вариационном ряду появляются
связки,
и значение ранга для некоторых элементов
определяется неоднозначно.
Связкой
размера
называется
подпоследовательность вариационного
ряда
такая,
что
и
Существует много способов обобщить определение ранга элемента на тот случай, когда в вариационном ряду имеются связки. Чаще всего применяется средний ранг.
Средним
рангом
наблюдения
называется
средний порядковый номер элементов той
связки
,
в которую попал элемент
:
.
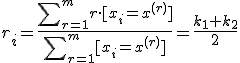Если
распределение, из которого взята выборка,
имеет плотность
то
совместное распределение всех элементов
вариационного ряда
задаётся
функцией
