
- •Основные понятия
- •Скалярное произведение векторов и его свойства
- •7.1. Определение векторного произведения
- •7.2. Свойства векторного произведения
- •7.3. Выражение векторного произведения через координаты
- •7.4. Некоторые приложения векторного произведения
- •Смешанное произведение трех векторов и его свойства
- •Краткий конспект лекции 13
- •Глава 5. Элементарная теория линейных операторов (продолжение)
- •5.3. Сопряженный оператор
- •5.3.1. Сопряженный оператор и его матрица
- •5.3.2. Самосопряженный оператор
- •5.3.3. Собственные значения и собственные векторы самосопряженного оператора
- •5.3.4. Приведение матрицы линейного оператора к диагональной форме
- •Бесконечно малая величина
- •Бесконечно большая величина
- •Свойства бесконечно малых
- •Связь бесконечно малой и бесконечно большой величины
- •Сравнение бесконечно малых функций.
- •Эквивалентные величины Определение
- •Теорема
- •Локальные экстремумы
Краткий конспект лекции 13
Глава 5. Элементарная теория линейных операторов (продолжение)
5.3. Сопряженный оператор
5.3.1. Сопряженный оператор и его матрица 5.3.2. Самосопряженный оператор 5.3.3. Собственные значения и собственные векторы самосопряженного оператора 5.3.4. Приведение матрицы линейного оператора к диагональной форме
5.3.1. Сопряженный оператор и его матрица
Напомним, что в
евклидовом пространстве определено
скалярное произведение векторов
![]()
Определение.
Если существует такой оператор
B, что для любых
![]() и
и
![]() из
евклидова пространства E справедливо
из
евклидова пространства E справедливо
![]() ,
то оператор B называется
сопряженным оператором к оператору A
и обозначается A*:
,
то оператор B называется
сопряженным оператором к оператору A
и обозначается A*:
![]()
Теорема. Если A — линейный оператор в евклидовом пространстве E и A — его матрица в некотором ортонормированном базисе в E, то у оператора есть единственный сопряженный оператор, причем матрица сопряженного оператора в том же базисе — это матрица AT.
Теорема доказана на лекции.
Пример. Рассмотрим оператор U поворота пространства R2 на угол относительно начала координат против часовой стрелки:
![]()
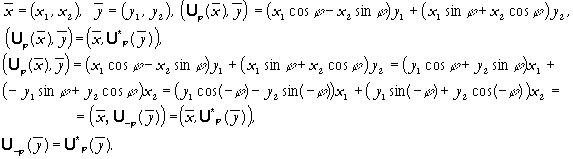 Т.е.
оператор, сопряженный оператору поворота
пространства R2 на угол
относительно
начала координат против часовой стрелки
— оператор поворота пространства R2
на угол -
относительно начала координат против
часовой стрелки.
Т.е.
оператор, сопряженный оператору поворота
пространства R2 на угол
относительно
начала координат против часовой стрелки
— оператор поворота пространства R2
на угол -
относительно начала координат против
часовой стрелки.
Матрицы операторов поворота на угол и угол - имеют, соответственно, вид:
![]() Видно,
что
Видно,
что
![]()
Нетрудно доказать (на лекции доказано) следующие свойства сопряженного оператора:
что сопряженный к линейному оператру — линейный оператор;
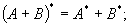
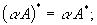
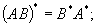
характеристические многочлены операторов
 и
и
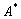
совпадают.
5.3.2. Самосопряженный оператор
Определение.
Если линейный оператор A,
действующий в евклидовом пространсте
E, таков, что для любых
и
из
E справедливо
![]() ,
то оператор A называется
самосопряженным оператором.
,
то оператор A называется
самосопряженным оператором.
Пример. Оператор
P2 — оператор проектирования
пространства R3 на подпространство
R2 параллельно вектору
![]() :
:
![]() .
.
Как показано выше,
матрица оператора P2 в
естественном ортонормированном базисе
![]()
Имеет вид
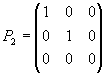
Тогда
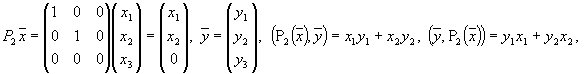 т.е.
т.е.
![]() —
оператор P2 —
самосопряженный оператор.
—
оператор P2 —
самосопряженный оператор.
Видно, что матрица P2 оператора P2 — симметричная матрица.
Нетрудно доказать следующие свойства самосопряженного оператора:
сумма самосопряженных операторов — самосопряженный оператор;
если оператор A самосопряженный оператор, то оператор
 —
тоже самосопряженный оператор (
—
тоже самосопряженный оператор (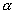 —
действительное число).
—
действительное число).
5.3.3. Собственные значения и собственные векторы самосопряженного оператора
Можно показать (на лекции не доказывается), что у самосопряженного оператора существует собственный ортонормированный базис.
Поскольку A=A*, то матрица самосопряженного оператора — симметричная матрица. Справедлива следующая теорема.
Теорема. Матрица самосопряженного оператора в собственном базисе имеет диагональную форму.
Ясно, что для того чтобы привести матрицу самосопряженного оператор к диагональному виду нужно найти собственные значения оператора и диагональную матрицу, на диагонали которой расположены собственные значения матрицы.
Если нужно записать
выражение для приведения матрицы к этой
диагональной форме, то нужно еще найти
собственные векторы матрицы, записать
матрицу C перехода к собственному
базису (матрицу, столбцами которой
являются координаты собственных векторов
оператора), найти обратную к ней матрицу
С-1 и тогда
![]() —
равенство, связывающее диагональну
форму
—
равенство, связывающее диагональну
форму
![]() матрицы
оператора в собственном базисе с матрицей
A оператора в заданном базисе.
матрицы
оператора в собственном базисе с матрицей
A оператора в заданном базисе.
