21. Расход жидкости

Расход потока жидкости (расход жидкости) – количество жидкости, протекающей в единицу времени через живое сечение потока.

Различают объёмный, массовый и весовой расходы жидкости.

Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м³/с, дм³/с или л/с. Он вычисляется по формуле , где     Q -  объёмный расход жидкости, V - объём жидкости, протекающий через живое сечение потока,    t – время течения жидкости.

Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле где      QM -  массовый расход жидкости, M -масса жидкости, протекающий через живое сечение потока,   t – время течения жидкости.

Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, КН/с. Формула для его определения выглядит так: где     QG -  весовой расход жидкости, G - вес жидкости, протекающий через живое сечение потока,   t – время течения жидкости.

Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости dQ.

22. Уравнение неразрывности

Уравнение неразрывности представляет собой закон сохранения массы вещества применительно к жидкостям. При соблюдении этого уравнения жидкость движется сплошным потоком без разрывов и пустот.

В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то можно записать: или где Q— расход жидкости, м³/с; v — средняя скорость в сечении при установившемся движении, м/с; S— площадь живого сечения, м²

Как следует из вышерассмотренного уравнения расход, проходящий через все живые сечения потока, неизменен, несмотря на то, что в каждом сечении средняя скорость и площадь живого сечения различны.

Это уравнение называют уравнением неразрывности потока при установившемся движении.

Из уравнения получим важное соотношение т. е. средние скорости обратно пропорциональны площадям живых сечений, которым соответствуют эти средние скорости.

Уравнение неразрывности потока — одно из основных уравнений гидродинамики. Оно выводится из уравнения неразрывности для элементарной струйки несжимаемой жидкости при установившемся движении: где v — местные скорости в каждом живом сечении струйки, м/с; DS — площадь живого сечения элементарной струйки, м²; D Qn— элементарный расход, м³/с

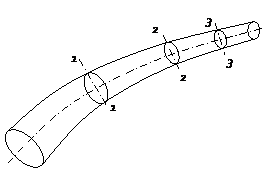
Рис.- схема демонстрирующая неразрывность потока

23. Средняя (расходная) скорость

Средняя скорость потока в данном сечении - воображаемая, фик­тивная скорость потока, одинаковая для всех точек данного живого се­чения, с которой через живое сечение проходил бы расход, равный фактическому.

Только в точках живых сечений, отстоящих от свободной поверх­ности примерно на 0,6 глубины и на 0,223r₀ от стенки в трубопроводе, местные скорости действительно равны средней скорости. В других же точках местные скорости больше или меньше средних.

При неравномерном движении средняя скорость в различных жи­вых сечениях по длине потока различна. При равномерном движении средняя скорость по длине потока постоянна во всех живых сечениях.

Если обратиться к формуле расхода потока ( ) и заменить в ней местные скорости u в каждой элементарной струйке средней скоростью, то полу­чим:

Последние три формулы очень важны и весьма часто используют­ся в гидравлических расчетах.