
- •Общие принципы получения информации в физических исследованиях. Основные цели обработки сигналов. Преимущества цифровых методов обработки сигналов. Примеры практического применения.
- •Содержание, этапы, методы и задачи цифровой обработки сигналов. Основные методы и алгоритмы цос.
- •Основные направления, задачи и алгоритмы цифровой обработки сигналов
- •Дискретные и цифровые сигналы. Основные дискретные последовательности теории цос.
- •Линейные дискретные системы с постоянными параметрами. Импульсная характеристика. Физическая реализуемость и устойчивость.
- •Линейные разностные уравнения с постоянными параметрами, их практическое значение и решение.
- •Соотношение между z-преобразованием и преобразованием Фурье
- •Обратное z-преобразование и методы его нахождения: на основе теоремы о вычетах, разложение на простые дроби и в степенной ряд.
- •Передаточная функция дискретных систем. Диаграммы нулей и полюсов. Условие устойчивости.
- •Частотная характеристика дискретных систем. Амплитудно-частотная и фазочастотная характеристики.
- •Фазовая и групповая задержка. Цифровая частота и единицы измерения частоты, которые используются в цифровой обработке сигналов.
- •Общая характеристика дискретного преобразования Фурье. Задачи, решаемые с помощью дпф. Дискретный ряд Фурье.
- •Дискретный ряд Фурье
- •Свойства дискретных рядов Фурье. Периодическая свертка двух последовательностей.
- •Дискретное преобразование Фурье. Основные свойства.
- •Общая характеристика ряда и интеграла Фурье, дискретного ряда Фурье и дискретного преобразования Фурье. Равенство Парсеваля.
- •Прямой метод вычисления дпф. Основные подходы к улучшению эффективности вычисления дпф.
- •Алгоритмы бпф с прореживанием по времени. Основные свойства.
- •Двоичная инверсия входной последовательности для
- •Алгоритмы бпф с прореживанием по частоте. Вычисление обратного дпф.
- •Вычисление периодической, круговой и линейной свертки. Алгоритм быстрой свертки. Вычислительная эффективность.
- •Вычисление линейной свертки с секционированием.
- •Амплитудный спектр, спектр мощности. Определение и алгоритмы получения.
- •Оценка спектра мощности на основе периодограммы. Свойства периодограммы. Методы получения состоятельных периодограммных оценок.
- •Основные проблемы цифрового спектрального анализа. Взвешивание. Свойства весовых функций. Модифицированные периодограммные оценки спм.
- •1.6.1. Просачивание спектральных составляющих и размывание спектра
- •Взвешивание. Свойства весовых функций
- •Паразитная амплитудная модуляция спектра
- •Эффекты конечной разрядности чисел в алгоритмах бпф
- •Метод модифицированных периодограмм
- •Метод Блэкмана и Тьюки получения оценки спектральной плотности мощности. Сравнительная оценка качества методов получения спм.
- •Сравнение методов оценки спектральной плотности мощности
- •Основные характеристики цифровых фильтров. Рекурсивные и нерекурсивные цифровые фильтры, их преимущества и недостатки.
- •Структурные схемы бих-фильтров (прямая и каноническая, последовательная и параллельная формы реализации).
- •Структурные схемы ких-фильтров (прямая, каскадная, с частотной выборкой, схемы фильтров с линейной фазой, на основе метода быстрой свертки).
- •Проектирование цифровых фильтров. Основные этапы и их краткая характеристика.
- •Расчет цифровых бих-фильтров по данным аналоговых фильтров. Этапы и требования к процедурам перехода.
- •Общая характеристика аналоговых фильтров-прототипов: Баттерворта, Чебышева I и II типа, Золоторева-Каура (эллиптические). Методика применения билинейного z-преобразования.
- •Эффекты конечной разрядности чисел в бих-фильтрах. Ошибки квантования коэффициентов, ошибки переполнения и округления. Предельные циклы.
- •Расчет цифровых ких-фильтров: методы взвешивания и частотной выборки.
- •Эффекты конечной разрядности чисел в ких-фильтрах.
- •Общая структурная схема системы цос. Дискретизация сигналов. Теорема отсчетов.
- •Погрешности дискретизации. Выбор частоты дискретизации в реальных условиях. Эффект наложения спектров
- •Дискретизация узкополосных сигналов
- •Выбор частоты дискретизации на практике
- •Квантование сигналов. Погрешность квантования. Отношение сигнал/шум и динамический диапазон при квантовании сигналов. Равномерное и неравномерное квантование
- •Анализ ошибок
- •Отношение сигнал/шум и динамический диапазон
- •Способы реализации алгоритмов и систем цос. Понятие реального времени обработки.
- •Особенности цос, влияющие на элементную базу, ориентированной на реализацию цифровых систем обработки сигналов.
- •Общие свойства процессоров цифровой обработки сигналов и особенности их архитектуры.
- •Архитектура Фон Неймана и гарвардская архитектура в пцос. Преимущества и недостатки.
- •Универсальные процессоры цос. Общая характеристика процессоров с фиксированной и плавающей точкой (запятой).
- •Основные различия между микроконтроллерами, микропроцессорами и сигнальными процессорами.
Общая характеристика ряда и интеграла Фурье, дискретного ряда Фурье и дискретного преобразования Фурье. Равенство Парсеваля.
1.4.2.2. Равенство Парсеваля. Пусть
имеются две последовательности конечной
длины
и
![]() ДПФ которых равны
ДПФ которых равны
![]() и
и
![]() соответственно. В этом случае
последовательность
можно представить в виде обратного
дискретного преобразования Фурье:
соответственно. В этом случае
последовательность
можно представить в виде обратного
дискретного преобразования Фурье:
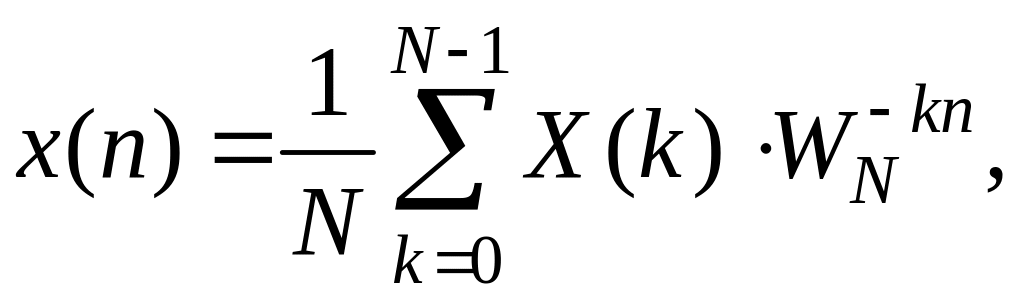
![]() (1.141)
(1.141)
Умножим правую и левую часть данного выражения на и найдём среднее значение полученного произведения:
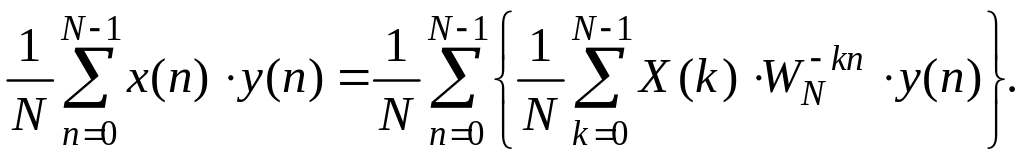 (1.142)
(1.142)
Изменив порядок суммирования в правой части последней формулы, получим:
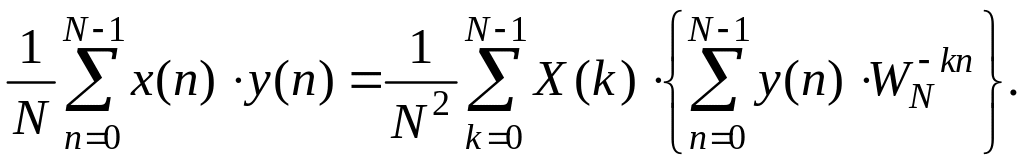 (1.143)
(1.143)
Так как
![]() (1.144)
(1.144)
то будем иметь:
 (1.145)
(1.145)
Если
![]() то
то
![]() и тогда
и тогда
 (1.146)
(1.146)
где
 – энергия сигнала, вычисленная по
переменной n
(во временной области), с новой
строки
– энергия сигнала, вычисленная по
переменной n
(во временной области), с новой
строки
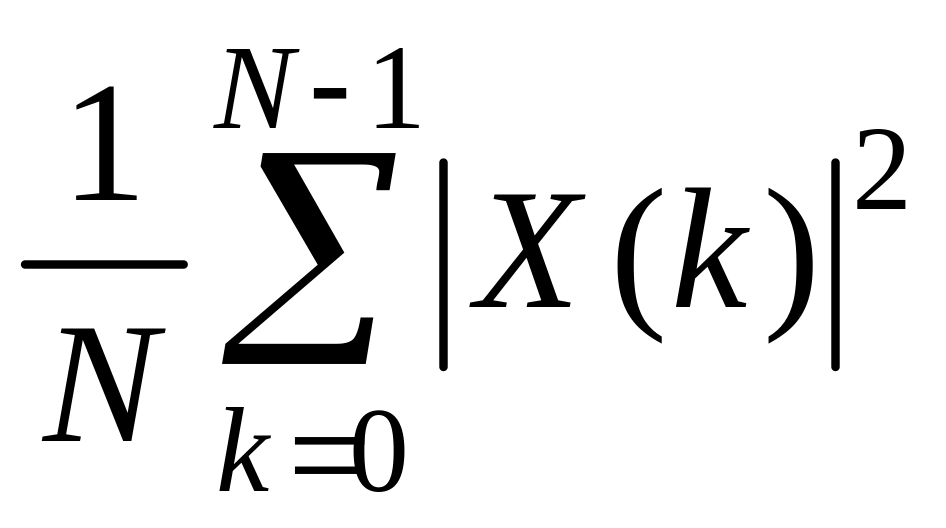 –
энергия сигнала, вычисленная по переменной
k (в
частотной области).
–
энергия сигнала, вычисленная по переменной
k (в
частотной области).
Это и есть равенство
(теорема) Парсеваля, устанавливающее
связь между энергией последовательности
![]() и её преобразованием Фурье
и её преобразованием Фурье
Прямой метод вычисления дпф. Основные подходы к улучшению эффективности вычисления дпф.
Рассмотрим непосредственное вычисление прямого ДПФ
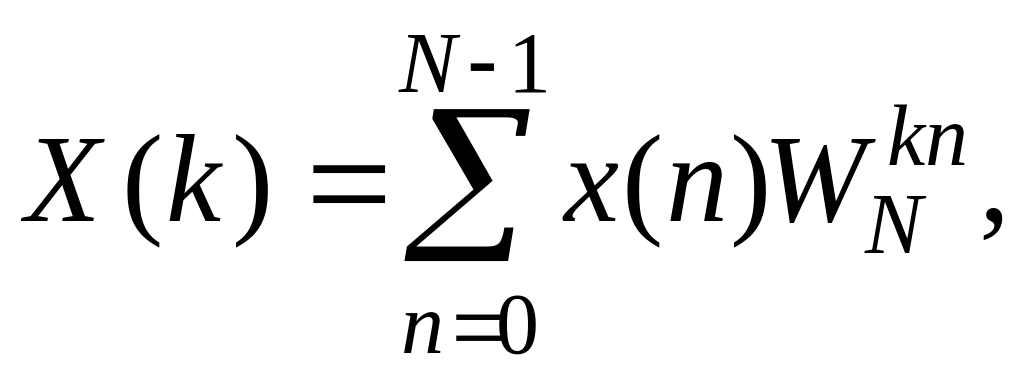 (1.147)
где
(1.147)
где
![]()
Выражение для X(k) можно представить в виде следующей системы уравнений:
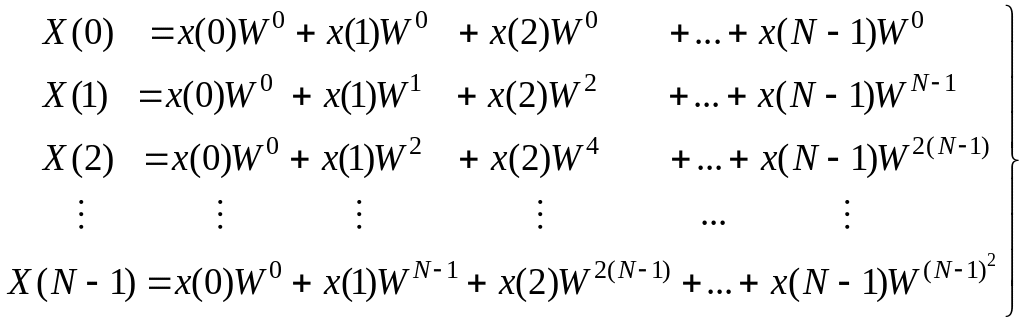 (1.148)
(1.148)
Видно, что для того, чтобы получить коэффициент X(0) необходимо выполнить N операций комплексного умножения и (N – 1) операцию комплексного сложения. Для получения X(1) требуется также N операций комплексного умножения и (N – 1) операций комплексного сложения.
Для того, чтобы вычислить два коэффициента X(0) и X(1) требуется 2N операций комплексного умножения и 2(N – 1) операция комплексного сложения.
Продолжив наши рассуждения дальше, получим, что, если требуется определить все N коэффициентов X(0), X(1), …, X(N – 1), то необходимо выполнить N2 операций комплексного умножения и N(N – 1) операций комплексного сложения. Представив (1.147) в виде последовательности операций над вещественными числами, получим откуда следует, что на каждое умножение комплексных чисел требуется четыре умножения и два сложения вещественных чисел, а каждое сложение комплексных чисел получается за счет сложения двух вещественных. Таким образом, при прямом вычислении одного значения ДПФ необходимо выполнения 4N вещественных умножений и (4N – 2) вещественных сложений. Для полного вычисления N-точечного ДПФ общее число умножений вещественных чисел достигнет 4N2, а сложений N(4N – 2).
Вдобавок к умножению и сложению при
вычислении ДПФ на универсальных или
специализированных ЭВМ необходимо
хранить N значений
входной последовательности x(n),
столько же комплексных экспонент
![]() и постоянно обращаться к ним в процессе
вычислений. Так как количество запоминаний
и обращений к памяти в вычислительных
алгоритмах обычно пропорционально
числу арифметических операций, то это
число считается разумной мерой сложности
вычислительного алгоритма или
времени, необходимого для выполнения
вычислений. Поскольку количество
операций, а, следовательно, и время
вычислений приблизительно пропорциональны
N2, то при прямом
методе вычисления ДПФ необходимое число
арифметических операций становится
весьма большим при больших значениях
N.
и постоянно обращаться к ним в процессе
вычислений. Так как количество запоминаний
и обращений к памяти в вычислительных
алгоритмах обычно пропорционально
числу арифметических операций, то это
число считается разумной мерой сложности
вычислительного алгоритма или
времени, необходимого для выполнения
вычислений. Поскольку количество
операций, а, следовательно, и время
вычислений приблизительно пропорциональны
N2, то при прямом
методе вычисления ДПФ необходимое число
арифметических операций становится
весьма большим при больших значениях
N.
