Программы как символьные преобразования Алфавит как тип данных
В реальных случаях автомат способен воспринимать лишь конечное множество событий, но очень большое. Без ограничения общности можно считать сообщение символами некоторого алфавита, а любой алгоритм – алгоритмом символьной обработки.
Замечание. «Можно без ограничения общности» здесь и далее означает «так проще определить, но неестественно и неудобно».
В соответствие с программистскими традициями определим алфавит как конечный порядковый тип. Множество слов в этом алфавите - это множество всех символьных последовательностей с операцией конкатенации. Последовательность длины ноль называют пустым символом, иногда пустым словом и обозначают ^. Приписывание пустого символа на деле означает «не приписывание никакого слова». Естественно считать пустой символ признаком конца слова. Для отражения ситуации переопределим семантику потоковых операций:
eof(f) f(marker-1)=^
read(f,^) if f(marker-1)=^ then… {Можно читать признак конца потока, но не позже}
write(f,^) f(marker):=^;
Таким образом, автомат может стоять на месте, не изменяя значения маркера.
Программы как синхронные преобразования
За счёт выбора походящего типа tOutput передачу сообщений можно без ограничения общности считать синхронной, порождающей по одному входному символу один выходной , то есть программу можно считать покомпонентной функцией.
<i1 i2 i3 …..>
< o1 o2 o3 …..>
Замечание. Введение пустого символа на деле уже реализует некоторую асинхронность.
Тривиальное поведение
Предполагает одинаковую реализацию на каждое входное сообщение, то есть наличие единственной функции f: input output; ot=f(it)
procedure Primitive (input, output);
begin
while not eof(input) do
begin
read(input, iMessage);
oMessage:=f(iMessage);
write(output, oMessage);
end;
end;
Или:
case iMessage of
i1: oMessage:=o(i1);
………………….
in: oMessage:=o(in);
end;
Замечание. При подходящем представлении данных тривиальное поведение порождает нетривиальные алгоритмы.
Упражнение. При представлении натуральных чисел в унарной системе (палочками) счисления запрограммировать функцию-последователь (+1)(разделитель записей–пробел).
Нетривиальное поведение
Реализует не один, а несколько типов поведения.
ot=ft(it)
Если функции ft вообще никак не связаны, уместно говорить не о сложном, а хаотичном, или глупом, поведении. Правильное поведение определяется не столько текущим временем, сколько памятью о прошлых событиях. В терминологии теории автоматов поведение характеризуется внутренним состоянием объекта. В реальности такая оперативная память всегда конечна.
f
Конечный автомат Мили определяется как конечная процедура.
Proc.: tInput tState tOutput tState
tState – произвольное конечное множество имён состояний.
Либо пара функций:
tOutput: tInput tState tOutput
fNextState: tInput tState tState
Независимые функции выхода и функции перехода.
procedure SimpleLife (input, output);
var state: tState;
begin
state:=InitState;
while not eof(input) do
begin
read(input, iMessage);
oMessage:=fOutput(iMessage, state);
state:=fNextState(iMessage, fState);
write(output, oMessage);
end;
end;
Понятие автомата Мили точно описывает достаточно сложное поведение. В современном программировании оно часто служит единственным языком формального описания. Популярность его в значительной степени обусловлена наглядным представлением в виде размеченного графа, где вершины графа представляют состояния, а пара меток на рёбрах – входные и выходные символы.
Пример. Управление электронными часами.
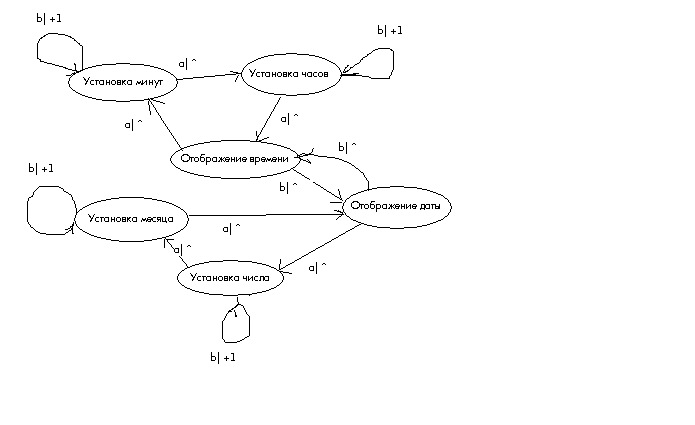
Упражнение. Построить конечный автомат, вычисляющий «предшественник» и сложение чисел в унарной системе.
Поскольку определение автомата включает лишь конечные функции, можно явно определить их разбором случаев (case), получив явную, или нормальную, форму.
Является ли эта форма действительно нормальной в смысле теоремы о нормальной форме, то есть любой ли алгоритм в принципе представим в виде конечного автомата?
Теория автоматов говорит «нет». Любой алгоритм, «сложнее» сложения, например, умножение чисел в представлении палочками не реализуется конечным автоматом. И всё-таки, при очень небольшом уточнении конечные автоматы являются универсальными вычислителями, то есть компьютерами. Более того, в некотором смысле, они реализуют не только все вычислимые функции, но и все алгоритмы, то есть все мыслимые правила разумного поведения.