Лекция 2 Математические модели систем автоматического регулирования

Математические модели описывают связи между входными и выходными сигналами элементов САР:

y(t) = F(x(t))

В теории автоматического регулирования используют следующие виды моделей:

• Дифференциальные уравнения:

(1).

Все производные берутся по времени t.

Дано: 1) x = x(t);

2) начальные условия: y|t=0=y0; y'|t=0=y'0; …; y(n-1)|t=0 = y'0.

Требуется найти y(t).

• Передаточные функции

• Частотные характеристики

• Переходные характеристики

Передаточные функции (ПФ)

Передаточные функции основаны на преобразовании Лапласа.

Пусть задана функция , которая удовлетворяет двум условиям:

1) f(t)≡0 при t< 0;

2) можно подобрать две константы “M” и “с” такие, что при функция удовлетворяет условию

Функция, удовлетворяющая условиям Дирихле, называется оригиналом.

Для любого оригинала существует несобственный интеграл:

F(p) = , (2)

Функция F(p) называется изображением по Лапласу оригинала f(t).

Связь оригинала с изображением обозначают:

f(t) F(p).

Имеются подробные таблицы соответствия оригиналов и изображений. Приведем некоторые соответствия:

1(t) 1/p (1(t)≡0 при t<0 и ≡1 при t≥1) ;

tⁿ n!/pⁿ⁺¹(n N);

е^–αt 1/(p+α);

sin ωt ω/(p²+ω²);

cos ωt p/(p²+ω²).

В теории преобразования Лапласа имеются теоремы:

1) Если f(t) F(p) и φ(t) ф(p),

то f(t)+ φ(t) F(p)+ ф(p).

2. Если f(t) F(p), то

cf(t) cF(p).

3) Теорема о дифференцировании оригинала:

Если f(t) F(p), то f'(t) pF(p)–f(0) (3)

Если, в частности, f(0) = 0, то

f'(t) pF(p). (4)

Применяя эту теорему и полагая, что все начальные условия нулевые

f'(0) = … = f^(n-1)(0) = 0,

получим : f ''(t) p²F(p),

………………., (5) f⁽ⁿ⁾(t) pⁿF(p).

Используя выражения (5) и предполагая, что уравнение (1) имеет нулевые начальные условия, преобразуем (1) к алгебраическому уравнению относительно изображений по Лапласу Y(p) и X(p):

(anpn + an-1pn-1 + … + a1p + + a0)Y(p) = (bmpm + … + b1p + b0)X(p);

Y(p) = (bmpm + … + b1p + b0)/ (anpn + an-1pn-1 + … + a1p + a0) *X(p) (6)

Отношение изображения по Лапласу выходного сигнала y(t) к изображению по Лапласу входного сигнала x(t) при нулевых начальных условиях

W(p) = Y(p)/X(p) (7)

называется передаточной функцией соответствующего звена (элемента) .

Из выражения (6) получаем связь передаточной функции с коэффициентами дифференциального уравнения (1):

W(p)= (bmpm + … + b1p + b0)/ (anpn + an-1pn-1 + … + a1p + a0) (8)

--------------------6 билет-------------------------

Структурные схемы САР и правила преобразования структурных схем

Структурной схемой САР называется такая схема, все элементы которой представлены своими передаточными функциями.

Структурные схемы можно преобразовывать с целью приведения к простейшему (каноническому) виду. Для этого используются следующие правила:

1) последовательное соединение элементов системы, где W(p) = W1(p)·W2(p)

2) параллельное соединение элементов, где W(p) = W1(p) + W2(p).

3) Антипараллельное соединение с отрицательной обратной связью

Y(p) = W1(p)·ε(p) = W1(p)·[X0(p) – Xос(p)] = W1(p)·[X0(p) – W2(p)·Y(p)],

тогда (1 + W1(p)·W2(p))·Y(p) = W1(p)·X0(p); Y(p) = X0(p) · W1 / (1 + W1·W2), отсюда эквивалентная передаточная функция

W(p) = W1(p) / (1 + W1(p)·W2(p))

Замечание: если обратная связь будет положительной, то знак в знаменателе будет заменен на «–».

4) Перенос звена через узел разветвления вперед (по ходу сигнала) – рисунок слева.

5) Перенос звена через узел разветвления назад – второй слева рисунок.

6) Перенос звена через узел суммирования вперед – третий рисунок.

7) Перенос звена через узел суммирования назад – четвертый рисунок.

--------------------11 билет------------------------

Передаточные функции разомкнутой и замкнутой САР

Используя правила (1–7), cтруктурную схему любой САР можно преобразовать к следующему каноническому (простейшему) виду, изображенному на рис.5, где передаточная функция Wрс(p) = Xос(p)/ε(p).

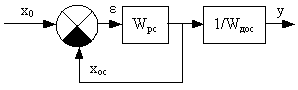
Рис.5. Каноническая структурная схема САР

Передаточная функция разомкнутой системы (ПФРС) – это отношение изображения по Лапласу сигнала обратной связи к изображению ошибки рассогласования при нулевых начальных условиях: Wрс(p) = Xос(p)/ε(p).

В общем случае ПФРС представляется как отношение двух полиномов (формула 8), где m≤n (условие физической реализуемости системы).

В зависимости от вида ПФРС различают 2 типа систем:

Если в выражении (8) и , система называется статической,

Если в выражении (8) , , система называется астатической,

Отношение изображения по Лапласу сигнала обратной связи к изображению по Лапласу задающего воздействия называется передаточной функцией замкнутой системы (ПФЗС):

Wзс(p)=Xос(p)/X0(p) = Wрс(p) / (1 + Wрс(p)). (9)

Замечание. Иногда удобно ПФЗС определять как отношение Y(p)/X0(p)=Wзс(y)(p); Wзс(y)(p)=Wзс(p)/Wдос(p), где Wдос(p) – передаточная функция датчика обратной связи.

хаpактеpистический полином – знаменатель ПФЗС (1 + Wрс(p)).

--------------------8 билет-------------------------