8.3. Обобщенный вектор трехфазной системы и замена переменных
Мгновенные
значения фазных величин трехфазной
системы можно получить, как проекции
трех фазных величин на одну ось времени,
так и проектируя один вектор на три оси
времени, сдвинутых на
.
Этот вектор носит
название обобщенного или изображающего
вектора (рис. 8.3).
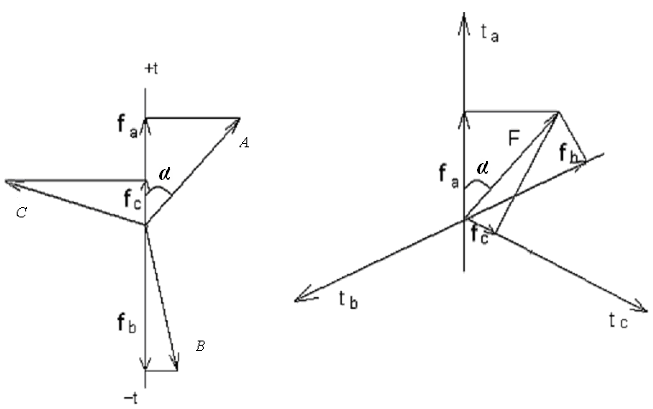
Рис. 8.3. Обобщенный вектор трехфазной системы
Связь между двумя системами определяется соотношениями:
Обобщенный вектор удобно представить в неподвижной декартовой системе координат xy. Такой способ носит название замены переменных. Число переменных при замене не изменяется. Связь между системами определяется соотношениями:
В симметричном режиме:
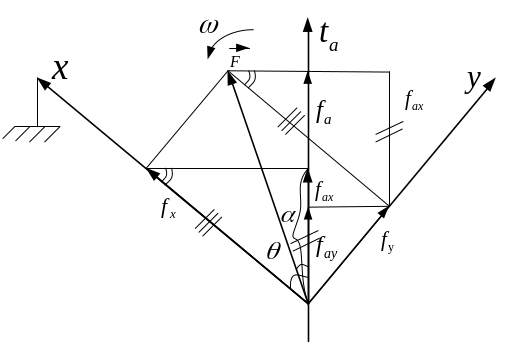
Рис. 8.4. Замена переменных
В
несимметричном режиме машины вводится
нулевая составляющая
.
При этом
.
(8.3)
−
частный
случай. Симметричный режим машины.
В декартовой системе координат (двухфазной машине) число коэффициентов собственных и взаимных индуктивностей уменьшилось, но не устранена переменность коэффициентов. Такая система координат осей х, у, неподвижных в пространстве, используется при анализе переходных процессов в несимметричных режимах синхронных машин. При анализе переходных процессов асинхронных машин вводятся оси, связанные с ротором при переменной скорости вращения. Такие оси носят название осей α, β.
Симметричные переходные процессы в синхронной машине целесообразно исследовать в системе координат, вращающихся вместе с ротором (ось х при этом совмещают с осью d ротора). Эта система осей называется осями d, q. Удобство системы координат, жестко связанных с ротором, для синхронной машины заключается в том, что для наблюдателя, вращающегося вместе с этими осями, машина в магнитном отношении оказывается симметричной независимо от положения ротора. То есть ротор вращается вместе со статором и ротор относительно статора остается неподвижным. В такой модельной машине невозможно образование ЭДС вращения, но они могут быть получены при обратном переходе от двухфазной машины к трехфазной.
Поэтому в системе координат d, q, потокосцепления уже не содержат переменных индуктивностей, а дифференциальные уравнения имеют постоянные коэффициенты, что существенно облегчает исследование. Преобразование к осям
d, q является практически единственным, приводящим дифференциальные уравнения синхронной машины с периодическими коэффициентами к уравнениям с постоянными коэффициентами. Это делает преобразование к осям d, q весьма важным, играющим фундаментальное значение в теории синхронной машины. Это преобразование было предложено Блонделем для установившегося режима и развито для переходных процессов Парком и Горевым. Уравнения носят название уравнений по огибающим (так как в новой системе координат и старой системе координат максимальные значения совпадают) или уравнений Парка−Горева.
Модель преобразованной машины представлена на рисунке 8.5. Если для этой
машины составить дифференциальные уравнения, то это будут дифференциальные уравнения с постоянными коэффициентами, которые можно будет решить и осуществить обратный переход к трехфазной машине по соотношениям (8.3).
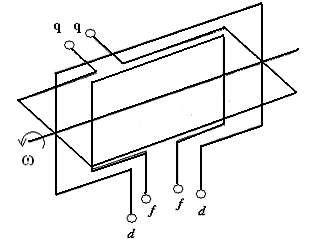
Рис. 8.5. Модель преобразованной синхронной машины
Потокосцепления модели и связь параметров модели и трехфазной машины:
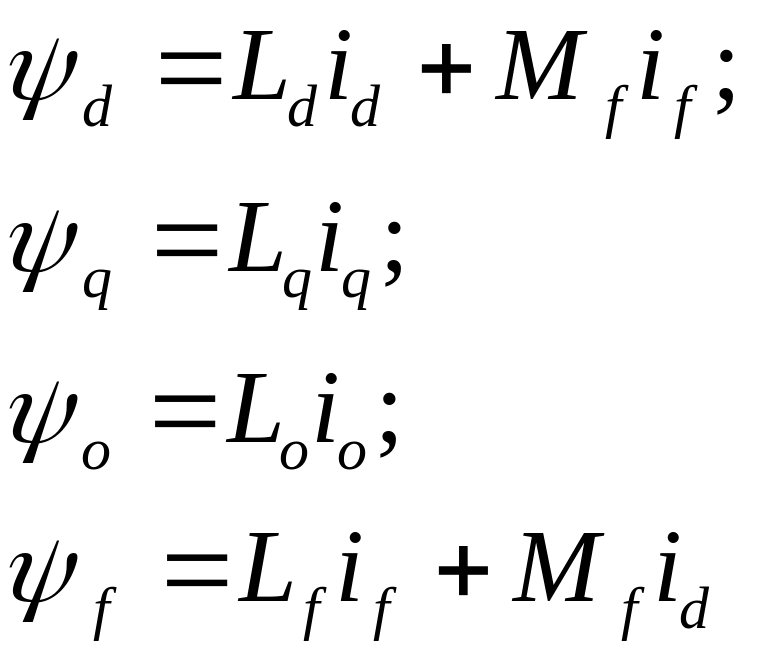
(8.4)