Файловый архив студентов. Файловый архив студентов.
1259 вузов, 4592 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Чистопольский (филиал «Восток» Казанского национального исследовательского технического университета имени А. Н. Туполева)
Предмет:
Вычислительная математика
Файл:

Лаба 3-4 по ВМ

.pdf
Скачиваний:
4
Добавлен:
21.03.2019
Размер:
235.26 Кб
Скачать
☆

ЛАБОРАТОРНАЯ РАБОТА №3-4. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ

УРАВНЕНИЙ

Цель работы: научиться решать системы нелинейных уравнений (СНУ) методом простых итераций (МПИ) и методом Ньютона с помощью ЭВМ.

Содержание работы:

1.Изучить МПИ и метод Ньютона для решения систем нелинейных уравнений.

2.На конкретном примере усвоить порядок решения систем нелинейных уравнений МПИ и методом Ньютона с помощью ЭВМ.

3.Составить программу и с ее помощью решить систему уравнений с точностью 0.001.

4.Изменить /100 и снова решить задачу. Сделать вывод о влиянии точности на количество итераций.

5.Составить отчет о проделанной работе.

ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ

Задание.

 

 

1. Аналитически решить СНУ вида:

 

 

f x, y x y 5 0;

 

1

 

(1)

f2 x, y xy 6

0.

 

2. Построить рабочие формулы МПИ и метода Ньютона для числен-

ного решения системы (1) при начальном приближении

 

x 0 , y 0 2,1 .

(2)

3. Составить программу на любом языке программирования, реализующую построенный итерационный процесс.

Решение.

1. Аналитическим решением СНУ (1) являются точки 2;3 и 3;2 .

2. Для построения рабочих формул МПИ для численного решения

системы (1) необходимо вначале привести ее к виду:

 

x 1 x, y

(3)

 

x, y

y 2

 

Для этого умножим первое уравнение системы (1) на неизвестную постоянную , второе - на , затем сложим их и добавим в обе части

уравнения x . Получим первое уравнение преобразуемой системы

 

x x f1 x, y f2 x, y x x y 5 xy 6 ,

(4)

где 1 x, y x x y 5 xy 6 . Далее, умножим первое уравнение

121

системы (1) на неизвестную постоянную , второе - на , затем сложим их и добавим в обе части уравнения y . Тогда второе уравнение преобразуе-

мой системы будет иметь вид:

y y f1 x, y f2 x, y y x y 5 xy 6 , (5)

где 2 x, y y x y 5 xy 6 .

Неизвестные постоянные , , , определим из достаточных условий сходимости итерационного процесса:

 

 

 

 

1

 

 

 

 

 

2

 

 

 

1 и

 

 

1

 

 

 

2

 

1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

x

 

 

 

 

y

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Запишем эти условия более подробно:

 

 

 

 

 

 

 

 

 

f1

 

 

f 2

 

 

 

 

f1

 

f 2

 

1

 

1

 

 

 

x

 

 

x

 

x

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f1

 

 

f 2

 

 

 

 

f1

 

f 2

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

y

 

 

y

 

y

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Полагая равными нулю выражения под знаком модуля, получим систему линейных алгебраических уравнений (СЛАУ) 4 порядка с 4 неизвестными , , , :

 

 

 

 

 

 

 

 

 

1 f1

f2 0;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f1

 

 

 

 

f2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0;

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

x

 

 

 

 

(6)

 

 

 

 

 

 

 

 

 

 

 

 

f1

 

 

 

 

f2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0;

 

 

 

 

 

 

 

 

 

 

y

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f1

 

 

 

 

 

f2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

y

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для решения системы (6) необходимо вычислить частные производ-

ные

f1

,

f2

,

f1

, f2

:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

x

 

y

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f1

 

f1

1,

 

f2

y,

f2

x .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

y

 

 

 

x

 

 

 

 

 

 

y

 

Тогда СЛАУ (6) запишется так:

1 y 0;

y 0;

x 0;

1 x 0.

122

 

Решением этой системы являются следующие значения:

x

,

 

 

y x

1

 

 

y

1

 

 

 

 

 

 

 

 

 

,

 

 

,

 

 

 

. Тогда рабочие формулы (4), (5) для ре-

y x

x y

x y

шения СНУ (1) примут вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x x

 

 

x

 

x y 5

1

 

xy 6 ,

 

 

 

 

 

 

y

x

 

y x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y y

 

y

x y 5

1

 

xy 6 .

 

 

 

 

 

x

y

 

x y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для реализации на ЭВМ рабочие формулы можно переписать так:

x k 1 x k

 

 

x k

 

 

 

x k y k 5

 

 

 

1

 

 

 

x k y k 6

,

 

y

k

x

k

 

y

k

x

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y k 1 y k

 

 

y k

 

 

 

x k y k 5

 

 

 

1

 

 

 

x k y k 6 , k 0,1,2,...

 

x

k

y

k

 

x

k

y

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

После несложных преобразований данные формулы примут вид:

x k 1

x k y k 5x k 6

,

 

 

 

 

x k y k

 

 

y k 1

x k y k 5y k 6

, k 0,1,2,...

x k y k

 

 

 

 

Заметим, что если частные производные f1 , f2 , f1 , f2 мало изме-

x x y y

няются в окрестности начального приближения (2), то:

f1 f1 1,

f2 y

 

2;1

1, f2 x

 

2;1

2 .

 

 

x

y

x

 

y

 

 

 

 

 

 

 

 

 

 

Тогда СЛАУ (6) запишется так:

1 0;

0;

2 0;

1 2 0.

Решением этой системы являются точки 2 , 1, 1. То-

гда рабочие формулы (4), (5) МПИ для решения СНУ (1) примут вид: x x 2 x y 5 xy 6 ,

y y x y 5 xy 6 .

Для реализации на ЭВМ рабочие формулы можно переписать так:

123

x k 1 x k 2 x k y

k 5 x k y

k 6 ,

(7)

y k 1 y k x k y k 5 x k y k 6 , k 0,1,2,...

 

Итерационный процесс (7) можно начать, задав начальное приближение (2). Процесс (7) заканчивается при одновременном выполнении

двух условий:

 

xk 1

xk

 

и

 

 

 

yk 1 yk

 

 

. В этом случае значения

xk 1 и

 

 

 

 

yk 1 являются приближенным значением одного из решений СНУ (1).

3. Для построения рабочих формул метода Ньютона в виде

 

 

 

 

 

 

 

 

 

 

k 1

 

 

k

 

W 1

 

k f

 

k ,

(8)

 

 

 

 

 

 

 

 

x

x

x

x

 

 

 

 

 

 

 

, ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

 

 

 

f1

x1

f1 xn

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где W x

 

 

 

 

 

 

 

 

 

 

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

, ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

fn

x1

fn

 

 

 

 

 

x1k , , xnk

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xn

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

необходимо:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.

 

 

Найти

 

 

матрицу

 

частных

производных

f1

 

f1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

y

1

1

 

 

 

 

 

 

 

W x, y

f2

 

f2

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

y

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Найти определитель этой матрицы:

 

 

 

 

 

 

 

 

 

 

 

det W x, y x y .

 

 

 

 

 

3. Определить обратную матрицу:

 

 

 

 

 

W x, y

1

 

 

 

1

 

 

x

y T

1

 

x

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

det W x, y 1

1

 

x y

1

Проведя несложные преобразования получим рабочую формулу ме-

тода Ньютона (8) в виде:

 

x k y k 5x k 6 ,

 

 

 

 

 

 

 

 

 

 

x k 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x k

y k

 

 

 

 

 

 

 

 

 

 

 

 

y k 1

 

x k y k 5 y k 6

, k 0,1,...

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x k y k

 

 

 

 

 

3. Блок-схема МПИ и метода Ньютона для решения СНУ приведена на рисунке 1.

Решение: в результате решения СНУ (1) при начальном приближе-

нии (2) методом простых итераций с точностью 0.001 получено реше-

ние

x 2 , y 2 2.00000;3.00000 ,

а

методом

Ньютона

124

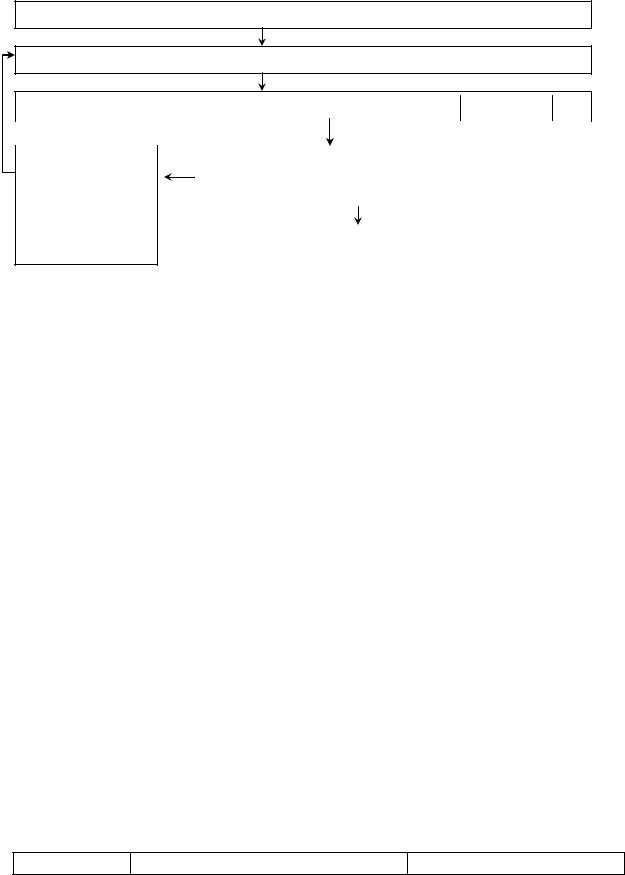
1.Задать параметры метода: k 0, x x 0 , y y 0 , .

2.Вычислить очередное приближение x k 1 , y k 1 по формулам (7).

3. Проверить условия окончания процесса: | x k 1 x k | & y k 1 y k .

 

 

 

 

 

 

да

 

 

 

4.

Обновить

на-

 

 

5. Распечатать приближенное значение

 

чальное приближе-

 

 

решения x k 1

 

k 1 .

 

нет

, y

 

ние

x k x k 1 ,

 

 

 

 

 

 

 

y k

y k 1

и

 

 

 

 

 

 

 

 

 

 

6. Останов

 

 

 

k k 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис.1

x 1 , y 1 2.00000;3.00000 .

4. Содержание отчета.

Отчет о проделанной работе должен содержать: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы (вывод итерационных формул); листинг программы; таблицу результатов; выводы о проделанной работе.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Определить аналитическое(ие) решение(я) исходной системы нелинейных уравнений.

2.Построить итерационные формулы, реализующие процесс поиска одного из решений системы нелинейных уравнений методом простых итераций и методом Ньютона.

3.Составить программу на любом языке программирования, реализующую построенные итерационные процессы, используя алгоритм методов, приведенный на рисунке 1. Печать результатов должна осуществляться на каждом шаге итераций в виде следующей таблицы:

k

x k

x k 1

 

 

x k 1 x k

 

 

y k

y k 1

 

 

y k 1 y k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.Провести вычислительные эксперименты.

5.Составить отчет о проделанной работе.

ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ

№ варианта Система нелинейных уравнений Начальное приближение

125

 

x y 4 0;

 

2,2

1.

 

 

 

 

 

 

 

 

 

 

 

xy 5

0

 

 

 

 

2.

x

2 y 2 4 0;

 

3,2

 

 

y 2 0

 

 

x

 

 

 

3.

x

2 y 2

5 0;

 

1,0

 

 

y 1 0

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x y 4 0;

 

 

 

 

 

 

1, 1

4.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x y

2

20 0

 

 

 

8

 

 

 

 

 

 

x y 2 0;

 

2, 4

5.

 

 

 

 

 

 

 

 

 

 

 

xy 3

0

 

 

 

 

 

x y 2 0;

 

1, 3

6.

 

 

 

 

 

 

 

 

 

 

 

xy 3

0

 

 

 

 

 

2x y 5 0;

 

1,1

7.

 

 

 

 

 

 

 

 

 

 

 

y x2 2

0

 

 

 

x 3y 5 0;

 

 

2, 1

8.

 

y2 1 0

 

 

 

x

 

 

 

 

x y 1 0;

 

1,1

9.

 

 

 

 

 

 

 

 

 

 

 

y x2 1

0

 

 

 

x y 1 0;

 

2,2

10.

 

 

y2

2

 

 

 

x

 

0

 

 

 

x

2 y 6 0;

 

1,1

11.

 

 

y 4 0

 

 

x

 

 

 

 

x y2 2 0;

 

2,2

12.

 

 

y 2 0

 

 

x

 

 

 

 

2x y 7 0;

 

2,2

13.

 

 

 

 

 

 

 

 

 

 

 

xy 6

0

 

 

 

 

 

x

2 y 2 17 0;

 

1,3

14.

 

 

 

 

 

 

 

 

 

 

 

3x y 1 0

 

 

 

x y 2xy 7 0;

1,0

15.

 

 

 

 

 

 

 

 

 

 

 

2x 2 y xy 8

0

 

126

 

 

2

xy

12

0;

 

 

y

 

1,3

16.

 

 

 

 

 

 

 

 

 

2

xy

3 0

 

 

x

 

 

 

x2 25y 2

0;

4,1

17.

 

 

 

 

 

 

 

 

xy 5 0

 

 

 

x

2 y 2 xy 7 0;

3,1

18.

 

y 1 0

 

 

x

 

 

 

 

y

2

2 0;

 

 

x

 

2,2

19.

 

 

 

 

 

 

 

 

 

2

y 2 0

 

 

x

 

 

20.

x

2 4 0;

 

1.8,1

 

3y 8 0

 

x

 

 

x

2 y2

9 0;

1,1

21.

 

y 3 0

 

 

x

 

 

127

Соседние файлы в предмете Вычислительная математика
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности