
Урок 1. Seminar_1_Proizvodnaya_integral-1
.pdfЭто всё то, что я рассказывал на семинаре. Если было понятно – можно просто пролистать.
Что такое функция
Величина y называется функцией переменной величины x, если каждому из тех значений, которые может принимать x, соответствует одно или несколько определенных значений y. При этом переменная величина x называется аргументом.
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции.
Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.
Разность между двумя значениями аргумента называется приращением аргумента и обозначается символом ∆х. Приращение может быть положительным, отрицательным и равным нулю. Если первое значение аргумента обозначить через х1, а второе через х2, то
∆х = х2 – х1
Разность между двумя значениями функции называется приращением функции: ∆у = у2 – у1 = f (х2) – f (х1).
Вычисление приращения любой функции у= f (х) удобно проводить в следующем порядке:

1.Даем аргументу х функции у= f (х) приращение ∆х, получаем точку х+∆х.
2.Находим значение функции в точке х+∆х у+∆у= f (х+∆х)
3.Из значения функции у+∆у вычитаем ее значение в точке х и находим приращение функции:
∆у= f (х+∆х) – f (х)
Предел функции Любой предел состоит из трех частей:
1)Всем известного значка предела  .
.
2)Записи под значком предела, в данном случае  . Запись читается «икс стремится к единице». Чаще всего – именно
. Запись читается «икс стремится к единице». Чаще всего – именно  , хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (
, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ( ).
).
3)Функции под знаком предела, в данном случае  .
.
Сама запись  читается так: «предел функции
читается так: «предел функции  при икс стремящемся к единице».
при икс стремящемся к единице».
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим
последовательность: сначала  , затем
, затем 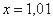 ,
,  , …,
, …,  , …. То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
, …. То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Готово.
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
Разбираемся, что такое 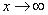 ? Это тот случай, когда
? Это тот случай, когда  неограниченно возрастает,
неограниченно возрастает,
то есть: сначала |
, потом |
, потом |
, затем |
и так далее |
до бесконечности. |
|
|
|
|
А что в это время происходит с функцией |
? |
|
||
, |
, |
, … |
|
|
Итак: если  , то функция
, то функция  стремится к минус бесконечности:
стремится к минус бесконечности:

Грубо говоря, согласно нашему первому правилу, мы вместо «икса»
подставляем в функцию  бесконечность и получаем ответ.
бесконечность и получаем ответ.
Еще один пример с бесконечностью:
Опять начинаем увеличивать 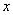 до бесконечности и смотрим на поведение функции:
до бесконечности и смотрим на поведение функции:
Вывод: при функция |
неограниченно возрастает: |
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
,  ,
,  ,
, 
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если  , попробуйте построить последовательность
, попробуйте построить последовательность  ,
, 
,  . Если
. Если 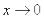 , то
, то  ,
,  ,
,  .
.
Обратите внимание! Строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим
числом вверху, да хоть с миллионом:  , то все равно
, то все равно  , так
, так
как рано или поздно «икс» начнёт принимать такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
Производная функции
Составим отношение приращения функции к приращению аргумента
Это отношение показывает, во сколько раз в данном интервале (x, x+∆x) приращение функции больше приращения аргумента, т.е. это отношение есть средняя скорость изменения функции относительно аргумента в данном интервале.
Если мы перейдем к пределу при ∆х→0, получим величину, равную скорости
изменения функции относительно аргумента в точке x. Этот предел  и называется производной от функции y (или просто производной функции) по аргументу x.
и называется производной от функции y (или просто производной функции) по аргументу x.

Производной функции y=f(x) при данном значении аргумента x называется предел отношения приращения функции ∆y к приращению аргумента ∆x, когда приращение аргумента стремится к нулю.
Таким образом, производная от функции y по аргументу x есть мгновенная скорость изменения функции относительно аргумента.
Пусть функция задана графически. Возьмём на кривой точку A(x,y) и дадим аргументу приращение ∆x. В результате функция получает приращение ∆y.
Проведем секущую AB и обозначим угол наклона секущей к оси Ох через ϕ. Из
рисунка 
При ∆х→0 точка B перемещается вдоль кривой, приближаясь к точке А. Секущая превращается в касательную к графику функции в точке А, имеющей угол наклона α к оси Ox
Производная функции равна тангенсу угла наклона касательной, проведенной к графику функции в точке, в которой находят производную.
Дифференциальные уравнения и их решение
Дифференциальные уравнения (ДУ). Эти два слова обычно приводят в ужас студентов.
Дифференциальное уравнение первого порядка в общем случае содержит:
1)независимую переменную  ;
;
2)зависимую переменную  (функцию);
(функцию);
3)первую производную функции:  .
.
В некоторых уравнениях 1-го порядка может отсутствовать «икс» или (и) «игрек», но это не существенно – важно чтобы в ДУ была первая производная  , и не было производных высших порядков –
, и не было производных высших порядков –  ,
,  и т.д.
и т.д.
Что значит решить дифференциальное уравнение? Решить дифференциальное уравнение – это значит, найти множество всех функций, которые удовлетворяют
данному уравнению. Такое множество функций часто имеет вид  (
( 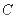 – произвольная постоянная), который называется общим решением дифференциального уравнения.
– произвольная постоянная), который называется общим решением дифференциального уравнения.

Пример 1
Решить дифференциальное уравнение  Полный боекомплект. С чего начать решение?
Полный боекомплект. С чего начать решение?
В первую очередь нужно переписать производную немного в другом виде.
Вспоминаем громоздкое обозначение  , которое многим из вас наверняка казалось нелепым и ненужным.
, которое многим из вас наверняка казалось нелепым и ненужным.
Итак:
На втором шаге смотрим, нельзя ли разделить переменные? Что значит разделить переменные? Грубо говоря, в левой части нам нужно оставить только «игреки», а в правой части организовать только «иксы». Разделение переменных выполняется с помощью «школьных» манипуляций: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т.п.
Дифференциалы 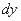 и
и  – это полноправные множители и активные участники боевых действий. В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:
– это полноправные множители и активные участники боевых действий. В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:
Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».
Следующий этап – интегрирование дифференциального уравнения. Всё просто,
навешиваем интегралы на обе части:
Разумеется, интегралы нужно взять. В данном случае они табличные:
Строго говоря, после того, как взяты интегралы, дифференциальное уравнение считается решённым. Единственное, у нас «игрек» не выражен через «икс», то есть решение представлено в неявном виде. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. То
есть,  – это общий интеграл.
– это общий интеграл.
Ответ в такой форме вполне приемлем, но нет ли варианта получше? Давайте попытаемся получить общее решение.
Пожалуйста, запомните первый технический приём, он очень распространен и часто применяется в практических заданиях: если в правой части после интегрирования появляется логарифм, то константу во многих случаях (но далеко не всегда!) тоже целесообразно записать под логарифмом.
То есть, ВМЕСТО записи  обычно пишут
обычно пишут  . Зачем это нужно? А для того, чтобы легче было выразить «игрек».
. Зачем это нужно? А для того, чтобы легче было выразить «игрек».
Используем свойство логарифмов  . В данном случае:
. В данном случае:

Теперь логарифмы и модули можно убрать:
Функция представлена в явном виде. Это и есть общее решение.
Ответ: общее решение:  .
.
Ответы многих дифференциальных уравнений довольно легко проверить. В нашем
случае это делается совсем просто, берём найденное решение  и дифференцируем его:
и дифференцируем его:
После чего подставляем  и производную
и производную  в исходное уравнение
в исходное уравнение  :
:
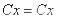 – получено верное равенство, значит, общее решение
– получено верное равенство, значит, общее решение  удовлетворяет уравнению
удовлетворяет уравнению  , что и требовалось проверить.
, что и требовалось проверить.
Придавая константе  различные значения, можно получить бесконечно много частных решений дифференциального уравнения. Ясно, что любая из
различные значения, можно получить бесконечно много частных решений дифференциального уравнения. Ясно, что любая из
функций  ,
,  ,
,  и т.д. удовлетворяет дифференциальному
и т.д. удовлетворяет дифференциальному
уравнению  .
.
Иногда общее решение называют семейством функций. В данном примере общее
решение  – это семейство линейных функций, а точнее, семейство прямых пропорциональностей.
– это семейство линейных функций, а точнее, семейство прямых пропорциональностей.
Общей чертой любых измерений является то, что ни одно из них невозможно произвести абсолютно точно из-за отсутствия идеально точных измерительных приборов, вследствие несовершенства органов чувств, несовершенства методики измерения. Иначе говоря, результат измерений всегда выражается приближенным числом или, как принято говорить, отягощен погрешностью.
Классификация погрешностей. Прямые и косвенные измерения
Следует различать три типа погрешностей: грубые или промахи, систематические и случайные погрешности измерений.
1.Грубые погрешности или промахи – это погрешности, резко выделяющие результат наблюдения из серии результатов, полученных в одинаковых условиях. Результат наблюдения, содержащий промах, должен быть исключен. Такие погрешности возникают из-за неправильного отсчета по прибору, неправильным записям (по невнимательности) и т.п.
2.К систематическим погрешностям относятся:
1)Погрешности, обусловленные несовершенством и неисправностью измерительного прибора (например, стрелка измерительного прибора может быть погнута). Измерительный прибор невозможно изготовить абсолютно точно хотя бы потому, что при его настройке и градуировке приходится производить измерения, а они отягощены погрешностями.
2)Погрешности, обусловленные несовершенством метода измерения. Чтобы избежать систематических погрешностей, нужно следить за исправностью приборов и критически относиться к методу измерения.
3. К случайным погрешностям относятся
1)Погрешности, обусловленные несовершенством органов чувств человека.
2)Погрешности, связанные с особенностями объекта и зависимостью измеряемой величины от контролируемых окружающих условий. Например, мы измеряли диаметр детали, а деталь в результате обработки нагрелась и имеет температуру выше комнатной, или сильно шероховатая. При измерениях в медицинской практике особенно важно учитывать отклонения параметров организма пациентов от средних значений в норме.
3)Погрешности, связанные с влиянием неконтролируемых внешних условий.
Все измерения можно разбить на два типа: прямые измерения и косвенные. Прямыми измерениями называются такие измерения, при которых непосредственно измеряется (сравнивается с мерой, эталоном) интересующая нас физическая величина. Например, измерение длины линейкой, измерение массы тела на весах и т.д.
Косвенными измерениями называются такие, при которых измеряется не сама интересующая нас величина, а другие величины, закономерно связанные с ней, результат измерения находится с помощью вычисления функциональной зависимости данной величины от других, которые были измерены непосредственно. Например, скорость ходьбы υ = t S . Непосредственно измеряли путь S и время t, а скорость υ подсчитывали по вышеприведенной формуле.
Абсолютная и относительная погрешности измерения
Для характеристики отклонения результата измерения от истинного значения измеряемой величины вводится понятие абсолютной погрешности. Абсолютная погрешность равна разности между полученным и истинным значениями (которое мы не знаем) измеренной величины.
Под относительной погрешностью (ε) измерения понимают отношение абсолютной погрешности к результату измерения. Относительную погрешность измеряют в относительных единицах или в процентах. Относительная погрешность характеризует степень точности конкретного измерения.
Оценка погрешностей прямых измерений
При прямом однократном измерении (непосредственному отсчету по прибору) за абсолютную погрешность принимают половину цены наименьшего деления шкалы прибора. Например, при измерении температуры был использован градусник, цена наименьшего деления которого равна 0,50 . Абсолютная погрешность, допускаемая при измерении, составит 0,250 .
При прямом многократном измерении получаем n значений измеряемой величины: Х1, Х2,. Х3, ….Хn. Результаты измерений обрабатываем по схеме:
1)Находим среднее значение измеренной величины как среднее арифметическое из значений полученных при отдельных измерениях.
2)Находим абсолютные погрешности отдельных измерений как разность между средним значением и значением, полученным при данном измерении: ∆Х1=Хср−Х1 ∆Х2=Хср−Х2 ……………. ∆Хn=Хср−Хn
3)Находим среднюю погрешность как среднее арифметическое из абсолютных значений абсолютных погрешностей отдельных измерений
Результат измерения записывается в виде: Х = (Хср ± ∆Хср)[ ] Здесь [ ] Х − единицы измерения величины Х.

Примеры для домашнего задания (в итоге должно быть 6 примеров по производным и 6 по интегралам)
Дальше материал, который можно распечатать и вложить\вклеить в тетрадь.

Производная функции
Составим отношение приращения функции к приращению аргумента
Это отношение показывает, во сколько раз в данном интервале (x, x+∆x) приращение функции больше приращения аргумента, т.е. это отношение есть средняя скорость изменения функции относительно аргумента в данном интервале.
Если мы перейдем к пределу при ∆х→0, получим величину, равную скорости изменения функции относительно аргумента в точке x. Этот
предел  и называется производной от функции y (или просто производной функции) по аргументу x.
и называется производной от функции y (или просто производной функции) по аргументу x.
Производной функции y=f(x) при данном значении аргумента x называется предел отношения приращения функции ∆y к приращению аргумента ∆x, когда приращение аргумента стремится к нулю.
Таким образом, производная от функции y по аргументу x есть мгновенная скорость изменения функции относительно аргумента.
Пусть функция задана графически. Возьмём на кривой точку A(x,y) и дадим аргументу приращение ∆x. В результате функция получает приращение ∆y.
Проведем секущую AB и обозначим угол наклона секущей к оси Ох через ϕ. Из рисунка 
При ∆х→0 точка B перемещается вдоль кривой, приближаясь к точке А. Секущая превращается в касательную к графику функции в точке А, имеющей угол наклона α к оси Ox
Производная функции равна тангенсу угла наклона касательной, проведенной к графику функции в точке, в которой находят производную.

Действия со степенями
Таблица
неопределенных
интегралов
