
ЦОС (1 лаб)
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Федеральное государственное образовательное бюджетное учреждение
высшего образования «Санкт-Петербургский государственный университет телекоммуникаций
им. проф. М. А. Бонч-Бруевича»
_____________________________________________________________________________
Кафедра радиосистем и обработки сигналов
Дисциплина «Цифровая обработка сигналов»
Лабораторная работа ЛР07
ДИСКРЕТНЫЕ СИГНАЛЫ
Выполнили: Проверил: Чернов И. Н.
Санкт-Петербург
Перемен
ная
|
N |
|
|
бр |
|
|
N |
|
|
T |
|
|
a |
|
|
C |
|
ωˆ 0 |
(рад) |
|
|
m |
|
|
U |
|
|
n |
|
|
0 |
|
|
n |
|
|
imp |
|
B |
, B |
, B |
1 |
2 |
3 |
ωˆ 1, ωˆ 2 , ωˆ 3
a1, a2 , a3
mean
var
СОДЕРЖАНИЕ ОТЧЕТА
ТАБЛИЦА ИСХОДНЫХ ДАННЫХ
Назначение |
|
|
|
Значение |
Идентификатор |
|||||||||||
Номер бригады |
|
|
|
|
N |
бр |
|
|
|
|
|
Nb = 1 |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Длина |
|
N = 30 + N |
бр |
mod 5 |
N = 32 |
|||||||||||
последовательности |
|
|||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Период |
T = 0, 0005(1 + Nбр mod 3) |
T = 0.0017 |
||||||||||||||
дискретизации |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Основание |
a = (−1)Nбр (0,8 + 0,005Nбр ) |
a = 0.805 |
||||||||||||||
экспоненты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Амплитуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С = 3 |
|
гармонического |
|
|
C =1 + N |
бр |
|
mod 5 |
||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
сигнала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частота |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w0 = pi/8 |
|
гармонического |
ωˆ |
0 |
= π (6 + N |
бр |
|
mod 5) |
||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
сигнала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задержка |
|
m = 5 + N |
бр |
mod 5 |
m = 7 |
|||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Амплитуда импульса |
|
|
|
U = N |
бр |
|
|
U = 1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Начальный момент |
|
n |
= N |
бр |
mod 5 + 3 |
n0 = 5 |
||||||||||
|
|
|||||||||||||||
импульса |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Длина импульса |
nimp = Nбр mod 5 + 5 |
n_imp = 7 |
||||||||||||||
Амплитуды |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гармонических |
|
B =1,5 + N |
|
|
|
|
mod 5 |
|
||||||||
|
|
1 |
|
|
|
|
|
бр |
|
|
|
Вектор |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
сигналов |
B |
|
= 5, 7 − N |
|
|
|
mod 5 |
|||||||||
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
бр |
|
|
B = [3.5 3.7 4.2] |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
B |
|
= 2, 2 + N |
|
|
|
mod 5 |
|||||||||
|
|
бр |
|
|||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||
Частоты |
ωˆ |
= π (4 + N |
бр |
mod 5) |
|
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
Вектор |
||||
гармонических |
ωˆ |
2 |
= π (8 + N |
бр |
|
mod 5) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
w = [pi/6 pi/10 pi/18] |
|||||
сигналов |
ωˆ |
|
= π (16 + N |
бр |
mod 5) |
|||||||||||
|
|
|
||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||
Коэффициенты |
|
a1 |
=1,5 − Nбр mod 5 |
Вектор |
||||||||||||
линейной комбинации |
a2 |
= 0, 7 + Nбр mod 5 |
||||||||||||||
гармонических |
A = [-0.5 2.7 3.4] |
|||||||||||||||
|
a |
=1, 4 + N |
|
|
|
|
mod 5 |
|||||||||
сигналов |
|
|
|
|
|
|
||||||||||
|
|
3 |
|
|
|
|
|
бр |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Математическое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mean = 5 |
|
ожидание |
mean = Nбр mod 5 + 3 |
|||||||||||||||
|
|
|||||||||||||||
Дисперсия |
|
var = Nбр mod 5 + 5 |
Var = 7 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
ПУНКТЫ ЗАДАНИЯ
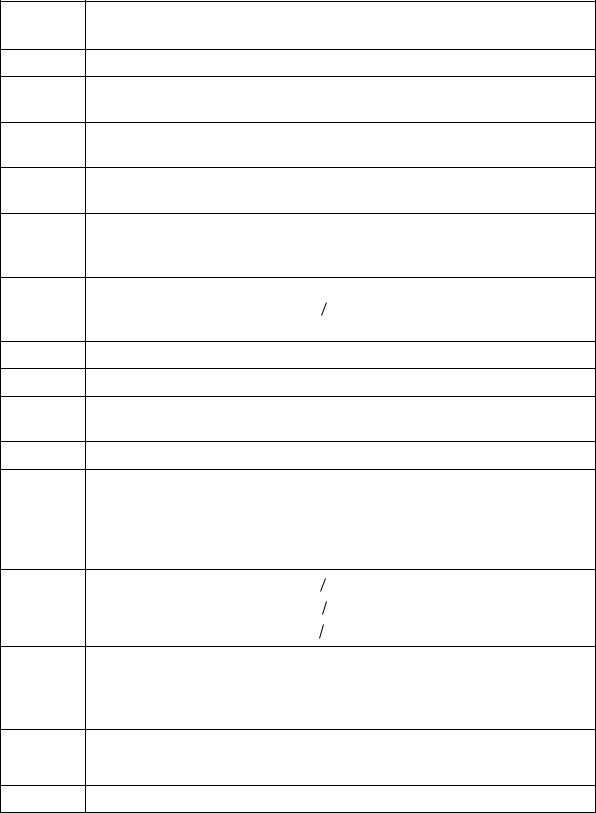
1. Цифровой единичный импульс 0( ) (идентификатор u0)
•Взаимосвязь между дискретным и дискретным нормированным временем.
Значения , где = 1 – период дискретизации.
д
Значение n: =
• Различие между цифровым единичным импульсом и дельта-функцией.
Цифровой единичный импульс. Это аналог дельта-функции для дискретных систем, но в отличие него, - физически реализуемый сигнал.
Дельта-функция (она же функция Дирака), используется в аналоговых системах.
ДОПОЛНИТЕЛЬНО:
Формула дельта-функции.
∞, = 0= { 0, ≠ 0
∞
∫ ( ) = 1
−∞
Эта функция бесконечно малой длительности, с бесконечным значением и площадью 1.
2. Цифровой единичный скачок 1( ) (идентификатор u1)
•Соответствие между цифровым и аналоговым единичными скачками.
Функция единичного скачка (она же функция Хевисайда, или функция включения), используется в аналоговых системах.
• Чему равна частота дискретизации цифрового единичного скачка.
д = |
1 |
= |
1 |
= 2кГц |
|
|
0,0005 |
||||
|
|
|
3
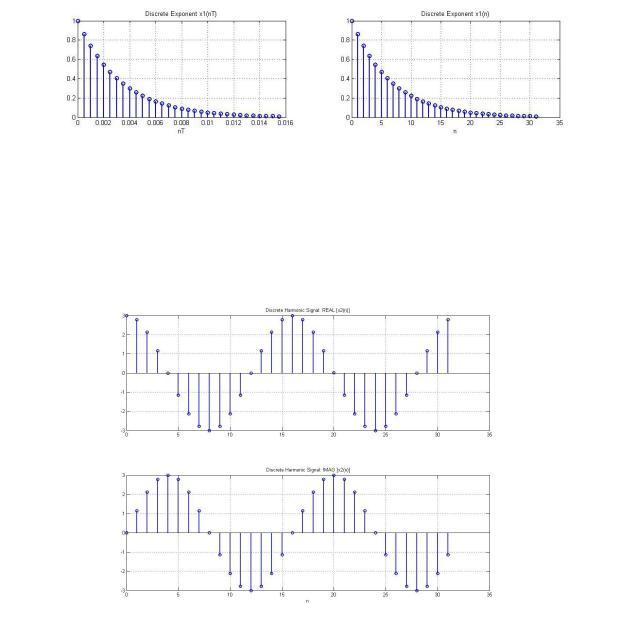
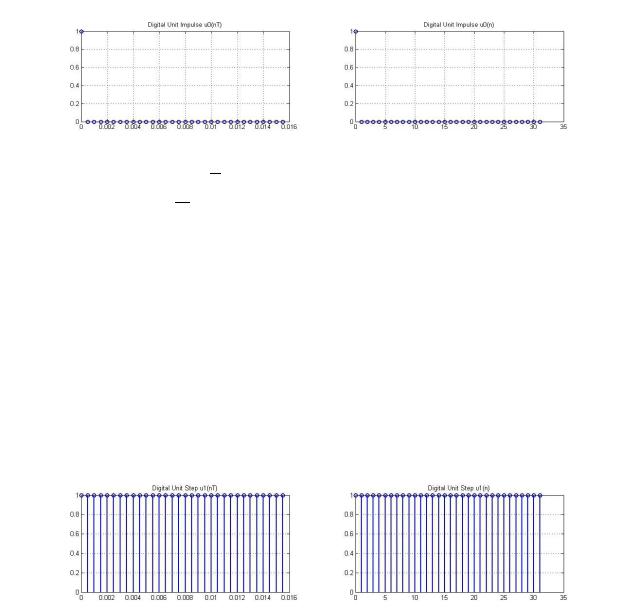
3. Дискретная экспонента 1( ) (идентификатор x1)
•Соответствие между дискретной и аналоговой экспонентами.
Вид дискретной экспоненты определяется величиной и знаком параметра a.
•Формула дискретной экспоненты в общем виде и со своими исходными данными.
( ) = { |
, ≥ 0 |
, ( ) = { |
0,805, ≥ 0 |
, < 0 |
0, < 0 |
4. Дискретный комплексный гармонический сигнал 2( ) (идентификатор x2)
•Сигнал в виде комбинации двух вещественных последовательностей.
( ) = ( ) = ;( ) = ( ) + ( );
|
( ) = 3 |
|
0,0017; |
|
|||
|
8 |
|
|||||
( ) = |
3 ( |
|
0,0017 ) + 3 ( |
|
0,0017 ) |
||
|
|
||||||
8 |
8 |
||||||
4
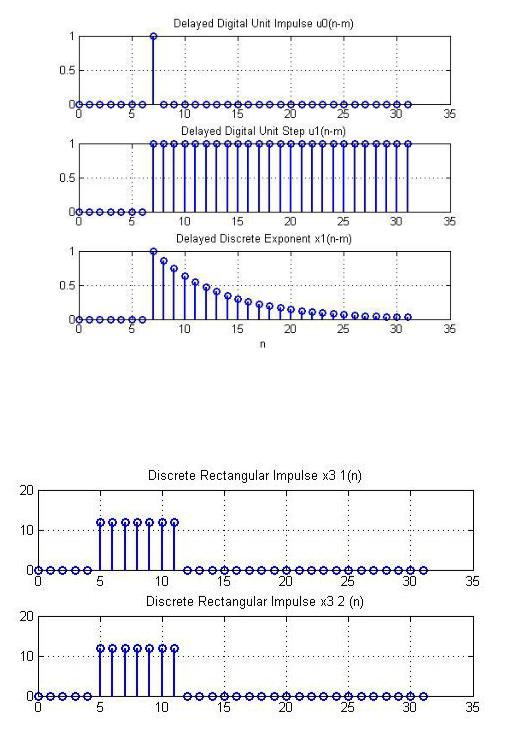
5. Задержанные последовательности
•Формула задержанных последовательностей.
0( − ) = {1, = |
; 1( − ) = {1, ≥ |
; ( − ) = {1, ≥ |
0, ≠ |
0, < |
0, < |
6. Дискретный прямоугольный импульс 3( )
•Изобразить от руки графики аналогового и дискретного прямоугольных импульсов и определить их длительность.
5
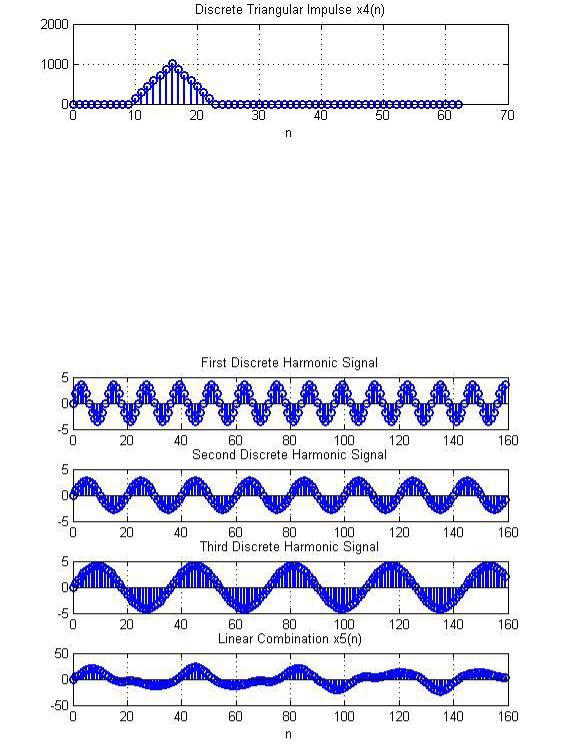
7. Дискретный треугольный импульс
•Аналитическая запись свёртки. Определить теоретически и по графику длину
свёртки L и ширину треугольного импульса.
∞
∑ ( ) ( − )
( ) = =0
∞
∑ ( ) ( − )
{ =0
8. Линейная комбинация дискретных гармонических сигналов 5( ) (идентификатор x5)
•Как определяют указанные характеристики.
6
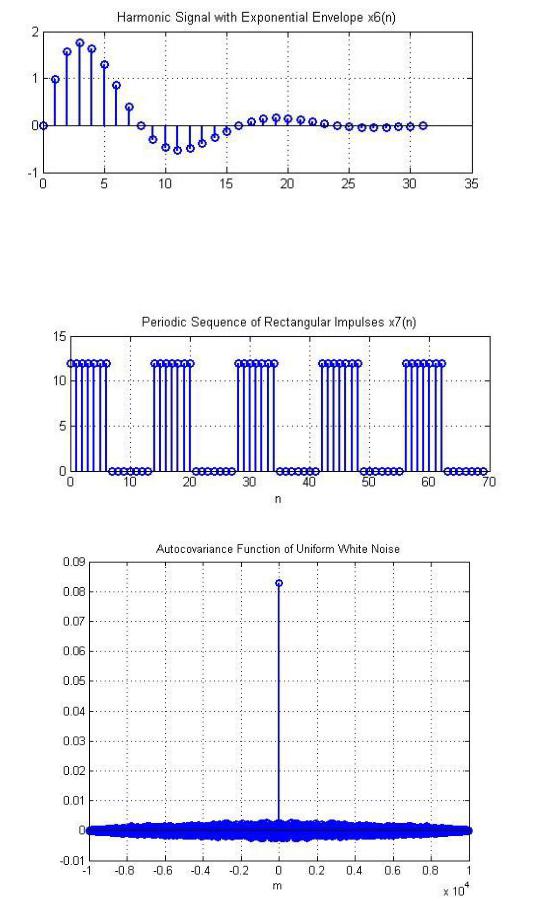
9. Дискретный гармонический сигнал с экспоненциальной огибающей.
Аналитическая формула дискретного сигнала 6( ):
∞
( ) = ∑ ( ) 0( − )
=0
10. Периодическая последовательность дискретных прямоугольных импульсов
11. Равномерный белый шум
• Чему равны истинные значения математического ожидания и дисперсии.
M(x)=0,49956; D(x)=0,08291
7
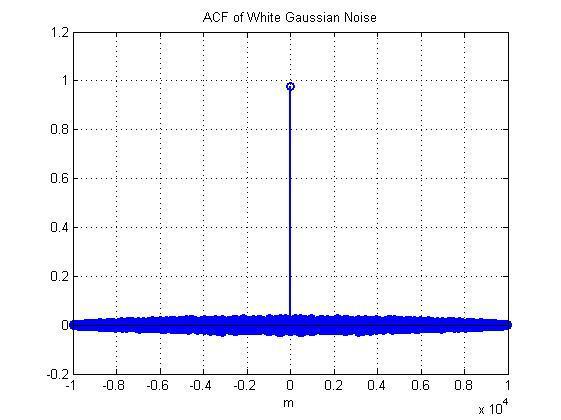
•Каков вид истинной автоковариационной функции.
Автоковариационная функция имеет цифрового единичного скачка
•Чему равна длина оценки автоковариационной функции.
Длина оценки: L=2N-1
Дополнительно:
Формула автоковариационной функции
|
1 |
−| |−1 |
|
|
|
( ) = |
∑ |
[ ( ) − ][ ( + ) − ] |
|||
|
|||||
|
|
|
|
|
|
=0
Позволяет оценить зависимость между отклонениями отсчетов последовательности от среднего значения при различных сдвигах по времени m.
12. Нормальный белый шум
•Чему равны истинные значения математического ожидания и дисперсии.
M(x)=0,0018848; D(x)=0,97902
•Каков вид истинной АКФ.
АКФ имеет вид цифрового единичного скачка.
• Чему равна длина оценки АКФ.
L=2N-1
АКФ позволяет оценить зависимость между её отсчётами при различных сдвигах по времени m:
|
1 |
−| |−1 |
|
( ) = |
∑ ( ) ( + ), −( − 1) ≤ ≤ ( − 1). |
||
|
|||
|
|
|
=0
8
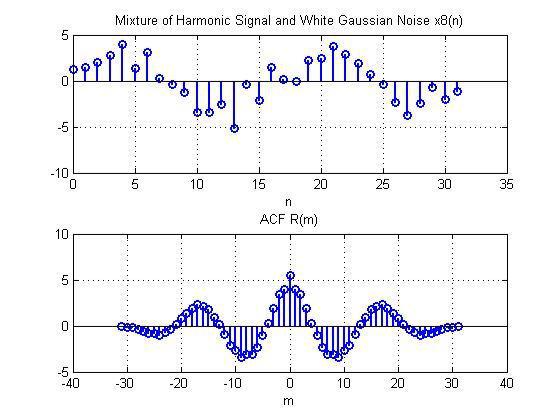
13.Аддитивная смесь 8( ) (идентификатор x8) дискретного гармонического сигнала x(n) с нормальным белым шумом с выводом графика на интервале времени.
•Понятие аддитивная смесь сигнала с шумом.
Аддитивная смесь сигнала с шумом – суммируется шум с полезным сигналом.
14.Оценка АКФ Rx(m) (идентификатор R) последовательности 8( ) с выводом графика АКФ, центрированной относительно m = 0.
•Свойства АКФ.
Являются чётными функциями длины L=2N-1, центрированными относительно m=0:
( ) = (− )( ) = (− )
при = 0 получаем равенства:
( ) = ( )(0) = (0) = 2
9
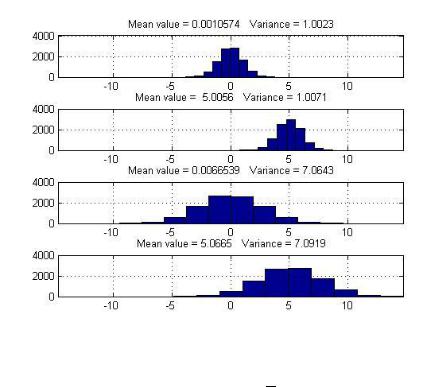
15. Нормальный белый шум с заданными статистическими характеристиками.
•К каким изменениям шума приводит изменение его математического ожидания и дисперсии.
= ∑ =0−1 ( ), 2 = 1 ∑ =0−1[ ( ) − ( )]2
Изменение математического ожидания и дисперсии приводит к изменению размаха и отклонению по оси х.
•Что отображает гистограмма и как она изменяется при изменении математического ожидания и дисперсии шума.
Дополнительно:
Гистограмма отражает нормальное распределение и как она изменяется при измерении математического ожидания и дисперсии шума происходит изменения высоты и отклонения по оси х.
Случайный сигнал – сигнал, значение которого в дискретные моменты времени n(или nT) заранее неизвестны и могут быть определены лишь с некоторыми вероятностями. Случайный сигнал называется эргодическим, если усреднение по множеству равно усреднению по времени.
10
