vostrikov

Отметим, что все нелинейности и действующие на объект внешние возмущения, отраженные в функциях f (t, y) и b(t, y) , подавляются

большим коэффициентом k , численные значения которого рекомендуется выбирать по соотношению

В этом случае точность обеспечения требуемых свойств (11.23) будет составлять

(0,05 0,01) f (t, y) ,

что соответствует обычной в практике 5%-ной зоне ошибок.

Полученный эффект объясняется структурной локализацией возмущений, что иллюстрирует схема системы, показанная на рис. 11.3.

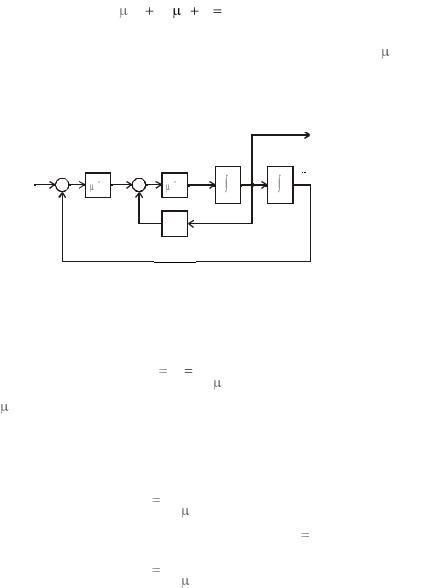
Рис. 11.3. Структурная иллюстрация метода

Как видим, система двухконтурная: внешний контур образован обычной обратной связью по выходной переменной, а внутренний – обратной связью по производной. Именно в нем локализовано влияние функций f (t, y) и b(t, y) , которое подавляется коэффициентом уси-

ления k .

Отметим, что внутренний контур является безынерционным, так как не содержит инерционных звеньев.

Для реализации закона (11.21) необходимо убедиться в том, что численные значения управления в любой момент времени не будут превышать имеющегося ресурса объекта. С этой целью исследуем управляющее воздействие в замкнутой системе, подставляя в (11.21) вместо y правую часть уравнения (11.19):

u k F ( ) f ( ) b( )u .

Отсюда следуют несколько важных выводов.

1.Асимптотическое управление (11.25) совпадает с управляющим воздействием (11.16), соответствующим точному решению поставленной задачи синтеза. Следовательно, основанный на методе локализации закон (11.21) представляет собой неявную реализацию «точного» управления (11.16).

2.Управляющее воздействие в замкнутой системе остается конечным даже при бесконечном коэффициенте усиления.

3.Выражение (11.25) позволяет определить максимальное значение управления в наихудшей ситуации, когда все функции достигают своих предельных значений

Больше этого значения управление в замкнутой системе быть не может. Если выполняется условие

то в ней можно обеспечить желаемые процессы (11.20).

11.3.2. ОЦЕНКА ВЛИЯНИЯ ПОМЕХ ИЗМЕРЕНИЯ

Выходная переменная физической системы измеряется датчиком, который всегда имеет некоторую помеху измерения. Как известно, дифференцирование усиливает влияние высокочастотных помех, поэтому в системах с законом управления (11.21) важно оценить их влияние.

С учетом (11.27) и (11.19) запишем управление в замкнутой системе

u k F ( ) f ( ) b( )u h

или после преобразований

uk F( ) f ( ) h . (11.29)

1b( )k

Впределе при k асимптотическое управление будет следующим:

определяет «вклад» помехи в управление. Сравнение (11.25) и (11.30) показывает, что при наличии помехи измерения может требоваться больший ресурс управления для объекта, чем без нее.

Выражение (11.30) следует иметь в виду при выборе датчика.

11.3.3. ДИФФЕРЕНЦИРУЮЩИЙ ФИЛЬТР

При практической реализации закона управления (11.21) необходимо оценивать производную y . С этой целью в систему следует доба-

вить специальное устройство, реализованное на интеграторах, которое будем называть дифференцирующим фильтром [8]. Он представляет собой динамическую систему первого порядка

выбираемую в зависимости от частотного состава и уровня помех измерения. Здесь yˆ – измеренное значение выходной переменной; –

малый параметр, отражающий инерционность фильтра.

Структурная схема дифференцирующего фильтра второго порядка показана на рис. 11.4.

yˆ x

a

2d2

a3

Рис. 11.4. Структурная интерпретация фильтра второго порядка

Поскольку дифференцирующий фильтр является линейным звеном, можно записать его передаточную функцию

где D( p) – характеристический полином фильтра, его будем назы-

вать также «фильтрующим» полиномом.

Покажем, что это устройство действительно позволяет получить оценку производной, выражение для которой с учетом (11.34) представим в виде

Так как p есть оператор дифференцирования, то py y и

точным значением. Таким образом, для реализации закона управления (11.21) необходимо использовать дифференцирующий фильтр с малой инерционностью. На практике достаточно, чтобы инерционность фильтра была на порядок меньше, чем основные процессы в системе.

Заметим, что наличие таких звеньев приводит к возникновению в системе разнотемповых процессов, причем для ее работоспособности быстрые движения должны быть устойчивыми.

11.3.4.АНАЛИЗ ВЛИЯНИЯ МАЛЫХ ИНЕРЦИОННОСТЕЙ

Спомощью метода разделения движений выделим медленные и быстрые процессы в системе с дифференцирующим фильтром (рис. 11.5).

Рис. 11.5. Структурная схема системы с фильтром

При использовании фильтра первого порядка уравнения замкнутой системы имеют вид

y f ( ) b( )k F ( ) yˆ ,

(11.35)

yˆ y yˆ.

Поскольку первое уравнение содержит производную в правой части, необходимо сначала представить описание в стандартной форме. С этой целью введем новую переменную

z 1( y yˆ)

и получим следующую математическую модель системы:

y f ( ) b( )k F ( ) z ,

(11.36)

z f ( ) b( )k F ( ) z z.

Выделим подсистему быстрых движений

Запишем характеристическое уравнение подсистемы быстрых движе-

ний (рис. 11.6)

yˆ

€

x& WWфф((pp))

Рис. 11.6. Структурная схема контура быстрых движений

В общем случае с учетом D( p) оно принимает вид

Как видим, контур быстрых движений линейный, поэтому для анализа устойчивости можно применять известные критерии устойчивости (см. главу 4). Если используется фильтр первого или второго порядка, то этот контур будет устойчив при любых положительных значениях b( ) .

движений можно записать в форме

1

D( p)

Рис. 11.8. Контур быстрых движений с учетом помехи измерения

Так как этот контур линейный и для него справедлив принцип суперпозиции, то определим реакцию u на воздействие h(t) :

где Wк ( p) – передаточная функция контура.

соответствующая асимптотическая логарифмическая амплитудночастотная характеристика представлена на рис. 11.10. Очевидно, что в этом случае высокочастотная помеха будет отфильтровываться контуром.

Обсудим задачу синтеза системы управления на основе метода локализации для объекта, математическая модель которого имеет вид уравнения произвольного порядка