Интерполяция функций
В науке существуют три способа задания функции:
-
Аналитический – в виде формулы
:
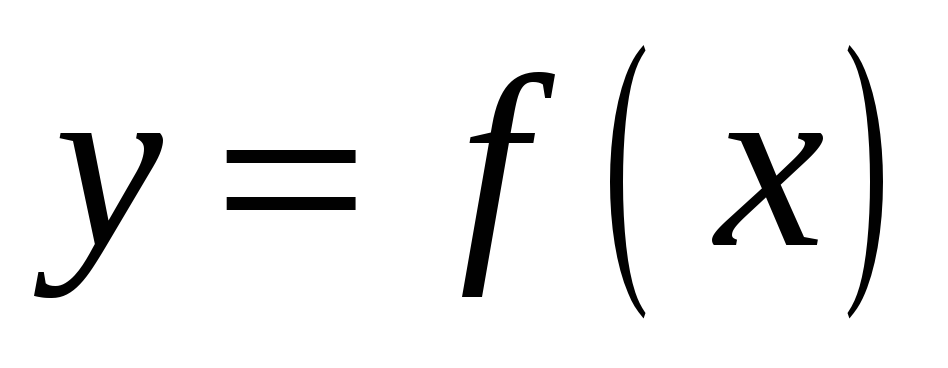«+» для любого значения аргумента можно вычислить значение функции
«-» вычисления могут быть достаточно сложными
«-» нет наглядности
-
Графический:
«+» наглядно
«-» малая степень точности при нахождении значения функции по графику
-
Табличный – распространен в физике, технике, экономике и чаще всего возникает в результате эксперимента. Также удобно задавать функцию таблично, если ее аналитическое выражение очень сложное. В этом случает просчитываются значения функции только в нескольких ключевых точках:
«+» для каждого значения аргумента из таблицы значение функции уже вычислено
«-» нельзя задать функцию на сплошном промежутке, т.е. вычислить значение функции в точке, которой нет в таблице
Пусть задана
таблица значений функции
для некоторых точек отрезка
:
|
|
|
|
|
… |
|
|
|
|
|
|
|
… |
|
|
Требуется построить
приближающую функцию
,
которая имеет достаточно простой вид
(принадлежит известному классу функций)
и принимает в узлах таблицы те же самые
значения, что и функция
,
т.е.
.
Поставленная
задача называется задачей
интерполяции, функция
называется интерполирующей,
узлы таблицы – узлами
интерполяции.
Для всех значений
аргумента
из таблицы справедливо равенство
,
для точек
,
отличных от узлов интерполяции (
)
значения данной и интерполирующей
функции примерно равны (равны с некоторой
степенью точности). Тогда отклонение
называется остаточным
членом интерполяции
и характеризует погрешность интерполирования
(в узловых точках погрешность интерполяции
равна 0!).
Наиболее часто интерполирующую функцию ищут в виде алгебраического (методы Лагранжа и Ньютона) или тригонометрического многочлена.
Теорема:
по таблице значений функции, содержащей
точку можно построить единственный
многочлен
степени
,
удовлетворяющий равенствам
.
Метод Лагранжа
Пусть функция
задана таблично:
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
Тогда интерполяционный многочлен Лагранжа имеет вид (степень интерполяционного многочлена на 1 меньше количества точек в таблице):
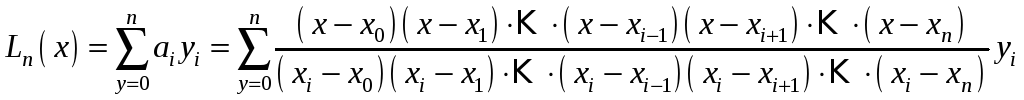
Пример:
|
|
0 |
2 |
4 |
6 |
|
|
5 |
4 |
7 |
3 |
Составим множители
Лагранжа
:
,
,
,
.
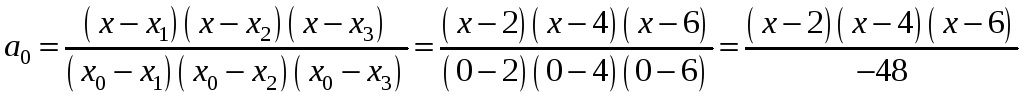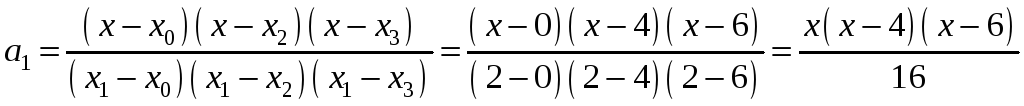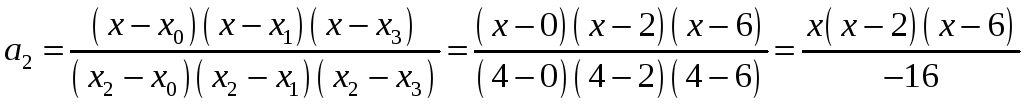Составляем многочлен Лагранжа:
.
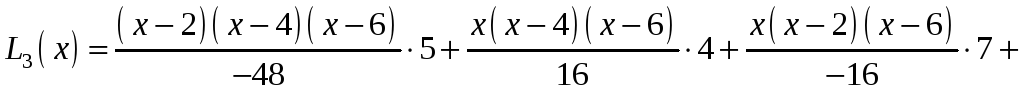
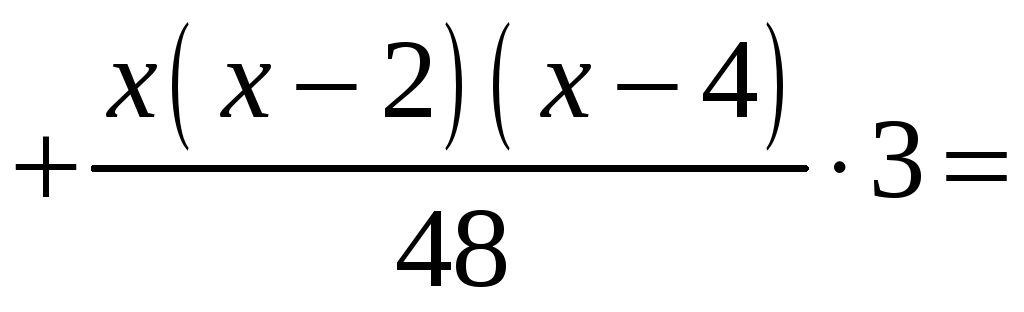
Замечание: если нет необходимости записывать интерполяционный многочлен в каноническом виде, а нужно просто вычислить значение функции в некоторой нетабличной точке, то удобнее подставить нужную точку в составленный многочлен в сокращенной форме:
.
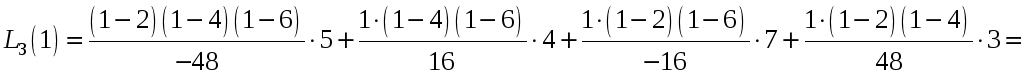
Метод Ньютона
Интерполяционный многочлен Ньютона строится только для таблицы с равноотстоящими точками.
.
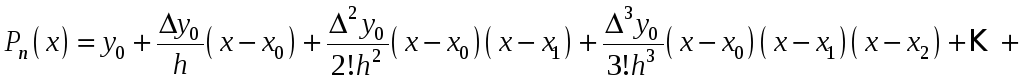
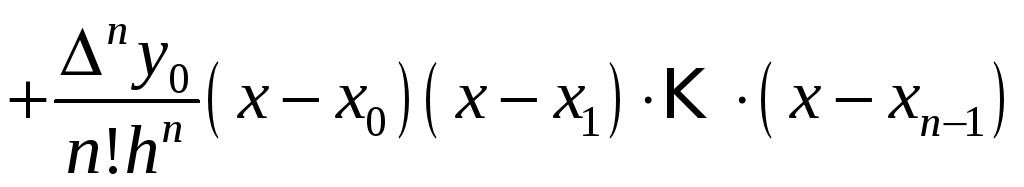Пример:
|
|
0 |
2 |
4 |
6 |
|
|
5 |
4 |
7 |
3 |
Составим таблицу конечных разностей:
|
|
|
|
|
|
|
0 |
5 |
-1 |
4 |
-11 |
|
2 |
4 |
3 |
-7 |
|
|
4 |
7 |
-4 |
|
|
|
6 |
3 |
|
|
|
Тогда многочлен Ньютона имеет вид:
Замечание:
по таблице из
точки можно составить многочлен степени
,
и притом только один. Поэтому
интерполяционные многочлены, составленные
по разным методам, должны совпадать!