37. Построение критической области.

Пусть вид распределения критерия k известен, p_k(x) – его плотность вероятности.

Построим правосторонней критическую область, исходя из уравнения значимости..

Вероятность попадания в заданный интервал вычисляется по формуле

;

В этом уравнении p_k(x) известно, – выбираем сами, поэтому всегда можем получить k_кр.

Найдем K_кр

тогда

Пусть критическая область двусторонняя и пусть p_k(x) – четная функция, тогда вероятность попадания в критическую область |k|>k_кр можем выразить через одностор.

p_k(x)dx = , то переходя в одностороннюю область p_k(x)dx =

38. Критерий согласия Пирсона.

Критерий проверки гипотез о предполагаемом виде распределения называется критерием согласия. Наиболее распространенный из них – критерий согласия Пирсона или критерий .(хи квадрат)

Пусть имеется независимая выборка (x₁,…., x_n) и пусть есть основание предположить,что он распределен по некоторой функции F(x).

Найдем максимальное x_max и минимальные x_min значения значение выборки, размах варьирования R= x_max–x_min.

Разобьем R на несколько частичных интервалов одинаковой длинны n:

k=3,32lg(n)

Пусть в результате получили интервалы z₀<z₁<…<z_k

Подсчитаем число вариант n_i попавших в i-ый интервал.

Исходя из предположения о виде распределения F(x) вычислим теоретические частоты.

На основании теоремы Бернулли

Сравним эмпирические и теоритические частоты с помощью случ величины.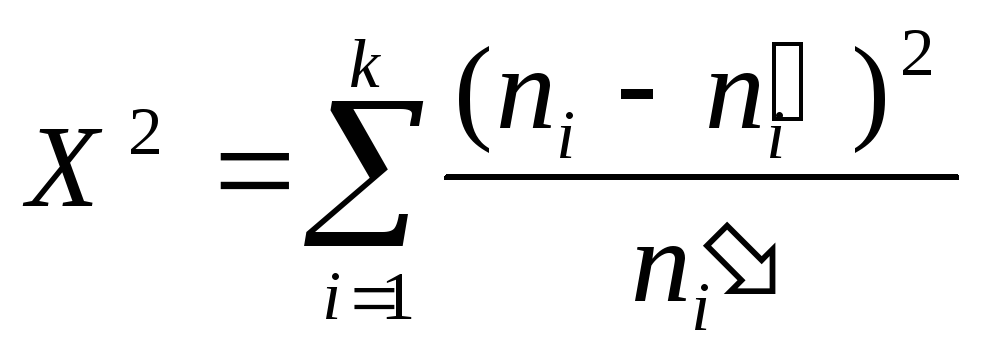

Можно показать, что при H₀ случайная величина имеет распределение (k-l-1) с числом степеней свободы (k-l-1).

Где k – число интервалов, l – число параметров предполагаемого распределения.

Проверка H₀ осуществляется следующим образом:

1. вычислить наблюдаемое значение критерия

2. по таблице критических точек распределения по выбранному уровню значимости и числу степеней свободы (k-l-1)находят_кр

а. Если _набл<_кр, то говорят, что нет основания отвергнуть H₀, следовательно признак X имеет распределение F(x).

б. Если _набл>_кр, то H₀ отвергаем и принимаем H₁.

Следовательно X имеет другое распределение.

Замечание:

Для того, чтобы эмпирическая функция распределения лучше приближалась к теоритической. Число интервалов k должно быть большим. Однако, построение критерия основано на немалых частотах n_i.Если некоторые частоты малы (<5), то соседние интервалы объединяются и соответствующие частоты складываются. В этом случае число степеней свободы уменьшается на 1.

39. Вычисление теоретических частот для нормального распределения.

Предположим, что признак Х имеет нормальное распределение. Находим x_max, x_min, R= x_max–x_min и z₀<z₁<…<z_k.

Перейдем к дискретному ряду для вычисления числовых характеристик, где Z_i^*– середины построенных интервалов

Для подсчета оценок параметров a и перейдем к дискретному ряду.

X			…
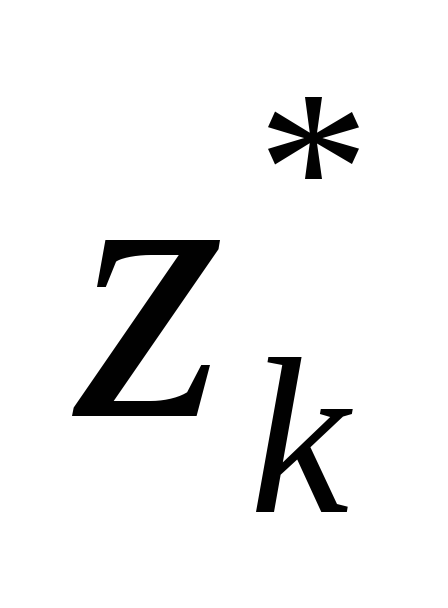
ni	n1	n2	…	nn

Найдем оценки параметров

1.

2. Счит вероятности попадания случ величины в построенные интервалы

3,Теоритическая частота

Постр табл

Замечания.

1. т.к. норм распределение принимает значения от –∞ до +∞, то будем считать, что

z₀=–∞, z_k=+∞

2. функция Лапласа нечетная и ассимптотическая

Ф₀(–z) = –Ф₀(z); Ф₀(+∞)=0,5