41. Дисперсия нормального закона распределения

Найдем дисперсию

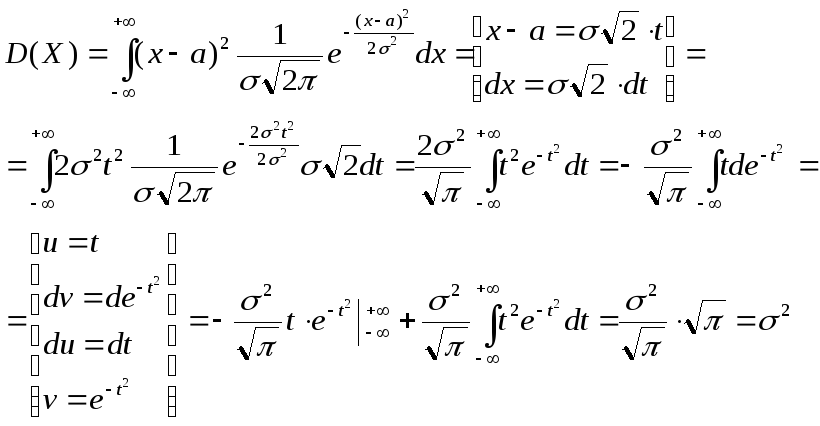
Таким образом, , , .

Мы установили вероятностный смысл параметров и а, а - это математическое ожидание распределения, - ее среднеквадратическое отклонение. По нормальному закону распределено большое количество случайных величин. Например, этому закону подчиняется распределение роста 20-ти летнего мужчины, вес женщины, рост которой равен 170 см, дальность полета снаряда, результат измерения длины, массы, времени и т.д.

42-43. Функция Лапласа и ее связь с функцией распределения нормальной случайной величины

Функция называется функцией Лапласа или интегралом вероятности. Она тесно связана с нормальным законом распределения. Ее основные свойства:

1. область определения функции Лапласа – вся числовая ось;

2. функция Лапласа монотонно возрастает на всей числовой прямой, т.к. ;

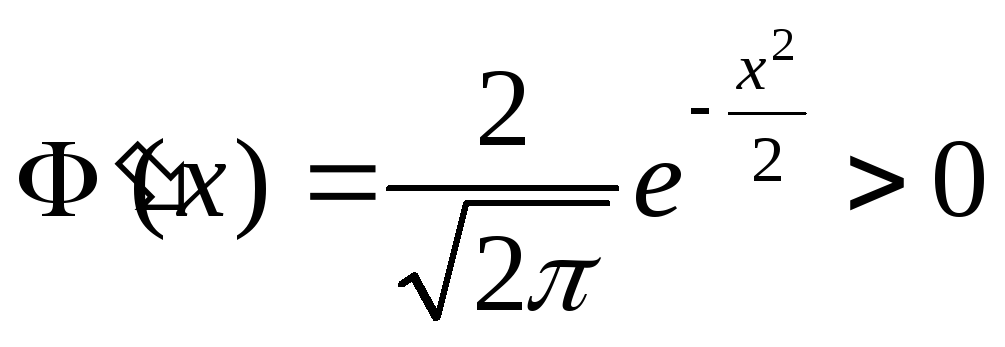3. функция 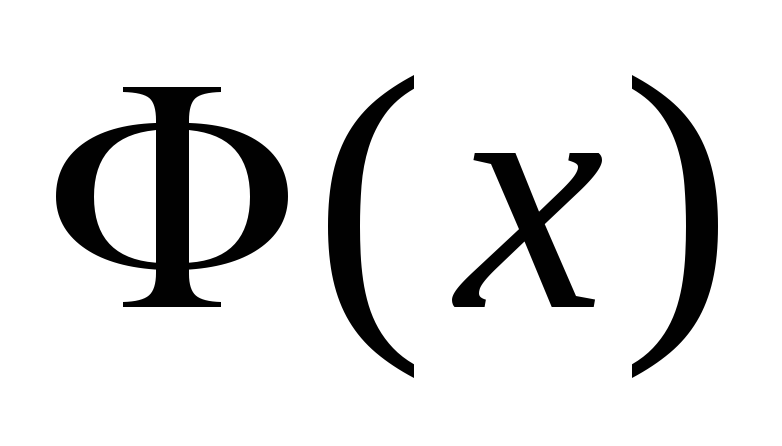- нечетная, покажем это.

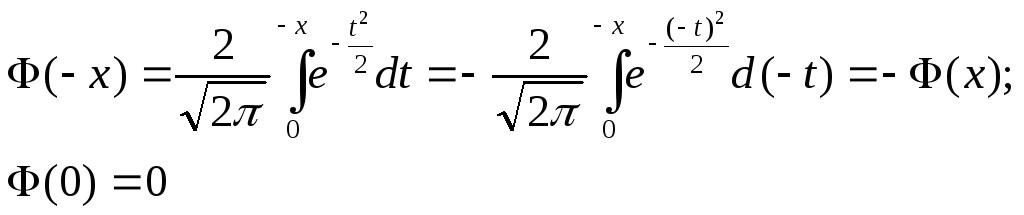
4) . Действительно,

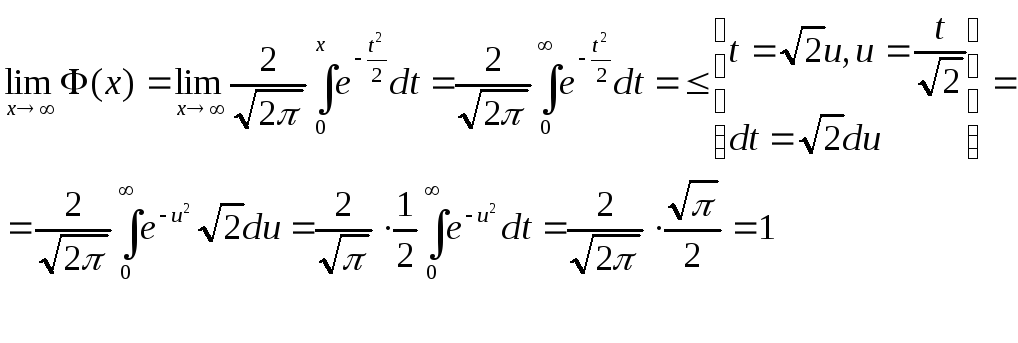
График.

Итак, пусть у нас имеется нормальная случайная величина X с математическим ожиданием а и дисперсией . Тогда функция распределения этой случайной величины

.

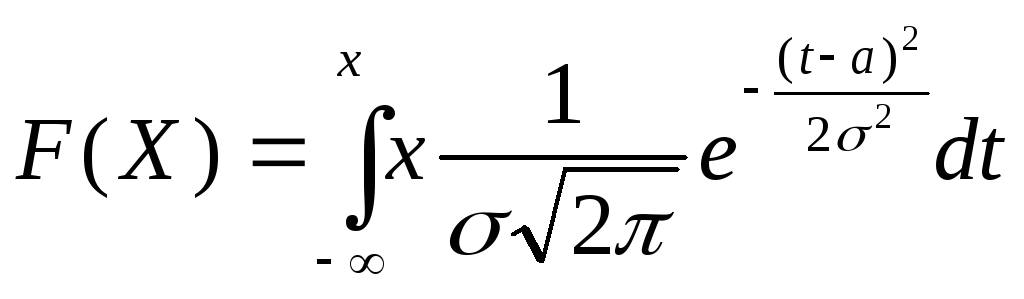Сделаем замену переменной в этом интеграле, положив . Тогда , при , , при , .

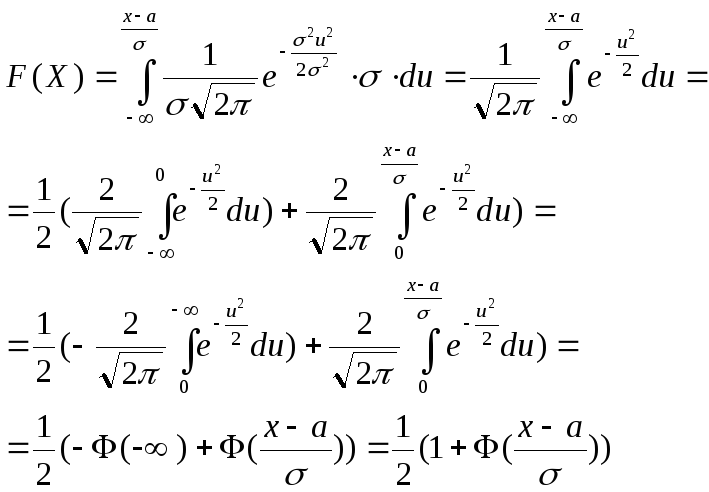
Если , то случайная величина называется нормированной. График функции распределения нормированной нормальной случайной величины с математическим ожиданием , т.е. имеет вид:

Найдем вероятность того, что случайная величина , распределенная по нормальному закону с параметрами , , примет значение из

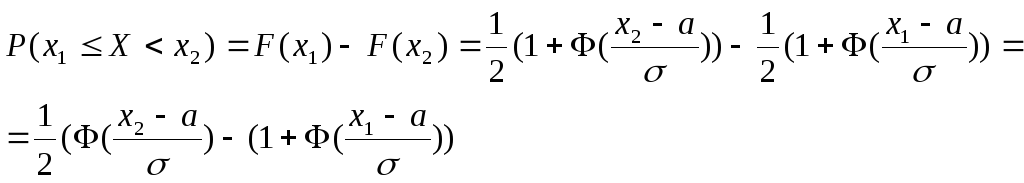
Таким образом,

.

Найдем вероятность того, что отклонение нормальной случайной величины от ее математического ожидания по модулю меньше некоторого положительного , т.е. найдем вероятность

.

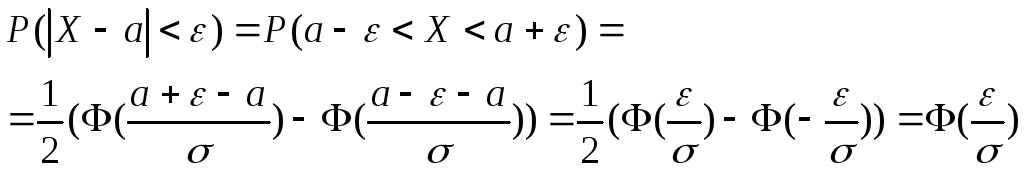
Итак: .

Вероятность того, что нормальная случайная величина отклоняется от своего математического ожидания по модулю меньше, чем на , определяется формулой

.

Если в этой формуле положить , то получим

.

Отсюда вытекает, что среди 10000 значений нормальной случайной величины в среднем только 27 выйдут за пределы интервала . Это означает, что практически среди небольшого числа значений нет таких, которые выходят за пределы указанного интервала. В этом и состоит правило «трех сигм», которое широко применяется в статистике.

44. Неравенство Маркова

Теорема. Если случайная величина может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина той же размерности, что и , всегда выполняется неравенство

.

Доказательство. Пусть - непрерывная случайная величина с плотностью распределения . Из условия теоремы следует, что при и при .

Математическое ожидание случайной величины -

(разобьем на два интеграла)

.

Так как , то .

Итак,

, .

Если это неравенство вычесть из тождества 1=1, то

или . Что и требовалось доказать.

Пример. Средний срок службы мотора 4 года. Оценить снизу вероятность того, что данный мотор не прослужит 20 лет.

Решение. Пусть случайная величина - срок службы мотора. Из условия задачи - . Требуется оценить снизу вероятность . Эту вероятность можно рассматривать как левую часть неравенства Маркова с . Тогда

.

Пример. Сумма всех вкладов в некотором сберегательном банке составляет 2 млн. рублей, вероятность того, что случайно взятый вклад не превышает 10000 руб. равна 0.8. Что можно сказать о числе вкладчиков данного сберегательного банка?

Решение. Пусть - величина случайно взятого вклада, а - число всех вкладчиков. Тогда из условия задачи следует, что . Так как , то по неравенству Маркова получим или

, , .