
- •1. Событие. Классификация событий
- •2. Вероятность события. Свойства вероятности. Классическая вероятность
- •3. Статистическое определение вероятности
- •4. Геометрическая вероятность
- •5. Задача о встрече
- •6. Действия над событиями
- •7. Теорема сложения вероятностей
- •8. Теорема умножения вероятностей
- •9. Условная вероятность события
- •10. Следствия из теоремы умножения вероятностей
- •11. Формула полной вероятности
- •12. Теорема гипотез. ( Формула Байеса )
- •13. Дискретные и непрерывные случайные величины
- •14. Закон распределения
- •15. Функция распределения
- •16. Общие свойства функции распределения
- •17. Плотность распределения
- •18. Основные свойства плотности распределения
- •19. Математическое ожидание и его свойства
- •20. Математическое ожидание непрерывной случайной величины
- •21. Мода и медиана
- •22. Дисперсия случайной величины
- •23. Свойства дисперсии
- •27. Условные законы распределения. Зависимые и независимые случайные величины
- •30. Корреляционный момент случайных величин и его свойства
- •31. Коэффициент корреляции и его свойства
- •32. Формула Бернулли
- •33. Наивероятнейшее число наступления события
- •34. Асимптотические формулы вычисления вероятностей
- •35. Биномиальный закон распределения
- •36. Закон распределения Пуассона
- •37. Равномерный закон распределения
- •38. Показательный закон распределения
- •39. Нормальный закон распределения
- •40. Математическое ожидание нормального закона распределения
- •41. Дисперсия нормального закона распределения
- •44. Неравенство Маркова
- •45. Неравенство Чебышева
- •46. Теорема Чебышева
- •47. Теорема Бернулли
- •48. Теорема Ляпунова
- •49. Интегральная теорема Лапласа
- •50. Виды статистических наблюдений
- •Виды статистических наблюдений:
- •51. Виды измерений
- •Количественные измерения
- •Порядковые (ранговые) измерения
- •Номинальные измерения
- •Статистические таблицы
- •52. Методы ранжирования
- •53. Группировка и табулирование количественных данных
- •54. Графическое изображение вариационных рядов
- •55. Показатели центра распределения (мода, медиана, среднее арифметическое, среднее гармоническое, среднее геометрическое)
- •56. Показатели вариации
- •57. Ассиметрия и эксцесс
- •58. Эмпирическая функция распределения
- •59. Точечные интервальные оценки
- •60. Доверительные интервалы
36. Закон распределения Пуассона
Случайная
величина
![]() ,
которая принимает значение
,
которая принимает значение
![]() с вероятностью
с вероятностью
![]() ,
,
где
![]() ,
,
![]() ,
называется распределенной по закону
Пуассона с параметром
,
называется распределенной по закону
Пуассона с параметром
![]() .
Этот закон может быть записан в виде
следующей таблицы:
.
Этот закон может быть записан в виде
следующей таблицы:
-
Значения
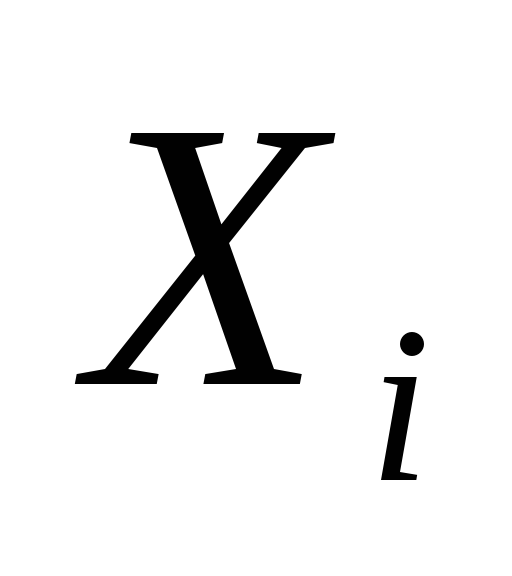
0
1
2
…
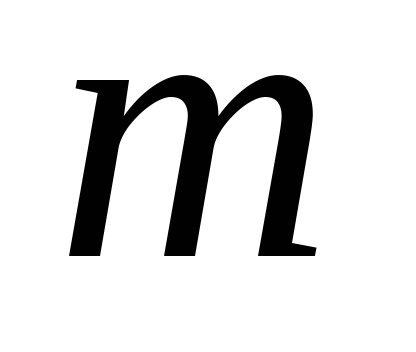
…
Вероятности

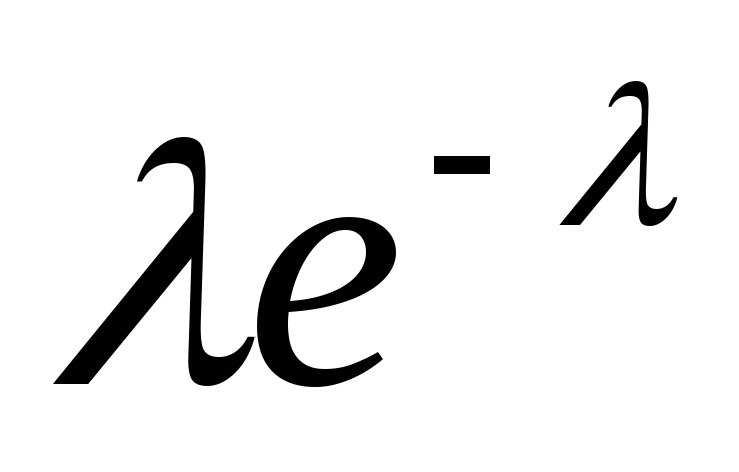
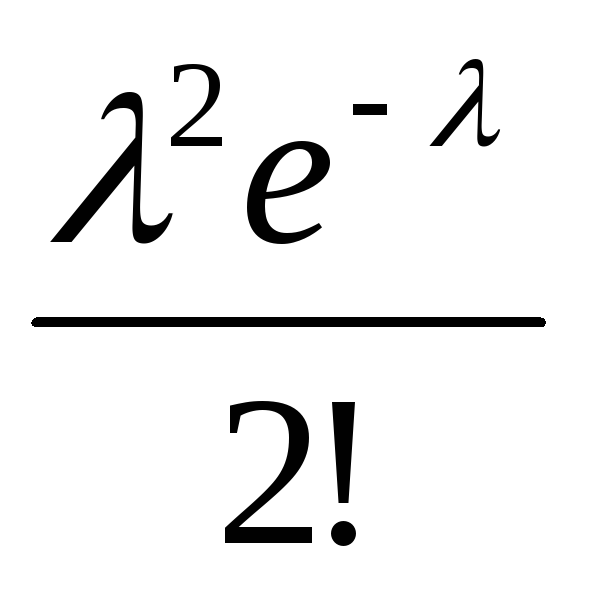
…
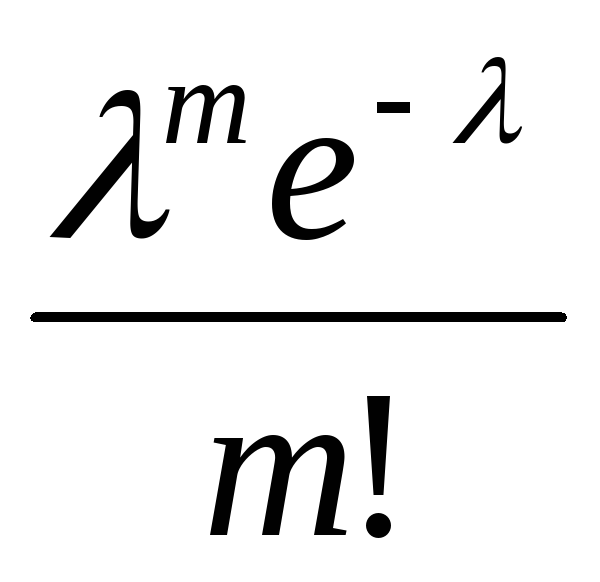
…
Данное
выше определение корректно. Действительно,
![]() и
и
![]() .
.
Найдем математическое ожидание и дисперсию данной случайной величины
![]() .
.
![]() ,
,
![]()
![]()
![]()
Таким
образом, если
![]() распределено по закону Пуассона с
параметром
распределено по закону Пуассона с
параметром
![]() ,
то
,
то
![]() .
.
Согласно
теореме Пуассона, распределение Пуассона
– это предельный случай биномиального
распределения, когда
![]() ,
,
![]() и
и
![]() .
По закону Пуассона распределены числа
так называемых редких явлений (например,
число рождения четверней, число вызовов
на АТС, поступивших в течение минуты,
число несчастных случаев на производстве
и т.д.).
.
По закону Пуассона распределены числа
так называемых редких явлений (например,
число рождения четверней, число вызовов
на АТС, поступивших в течение минуты,
число несчастных случаев на производстве
и т.д.).
37. Равномерный закон распределения
Непрерывная случайная величина, которая принимает значения только на сегменте [a,b] с постоянной плотностью распределения, называется распределенной по равномерному закону.
Из определения следует, что плотность распределения определяется равенством
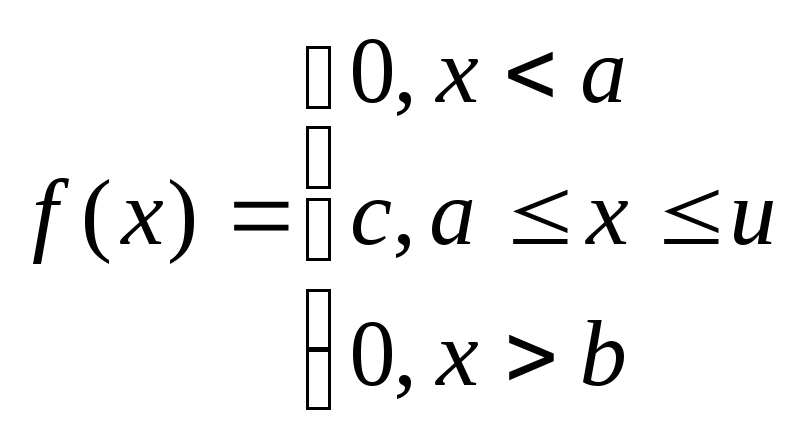
и должна удовлетворять двум требованиям:
1)
![]()
2)
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом
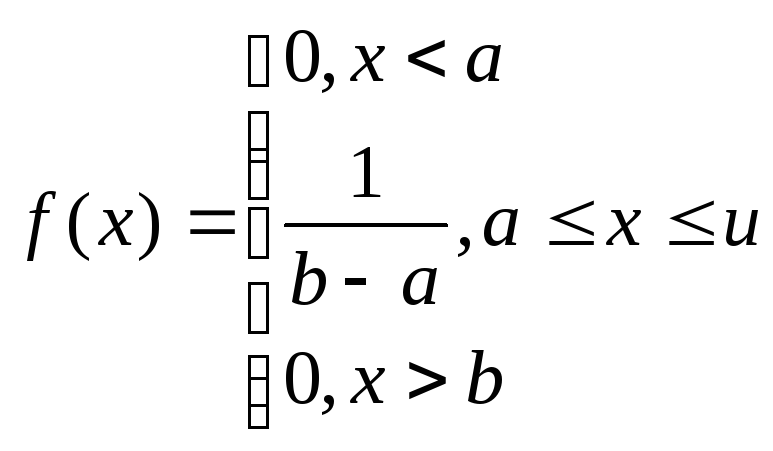
Найдем
функцию распределения данной случайной
величины. Известно, что
![]() ,
,
Тогда согласно формуле выше, получим
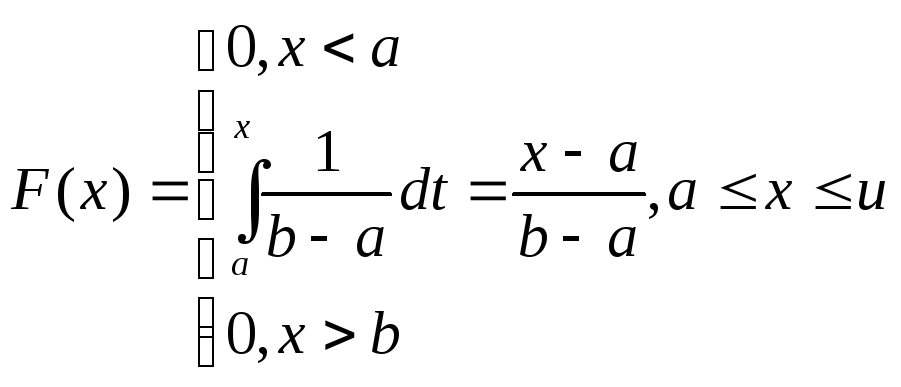
Графики
Найдем математическое ожидание и дисперсию случайной величины, распределенной равномерно на сегменте [a,b]:
![]()
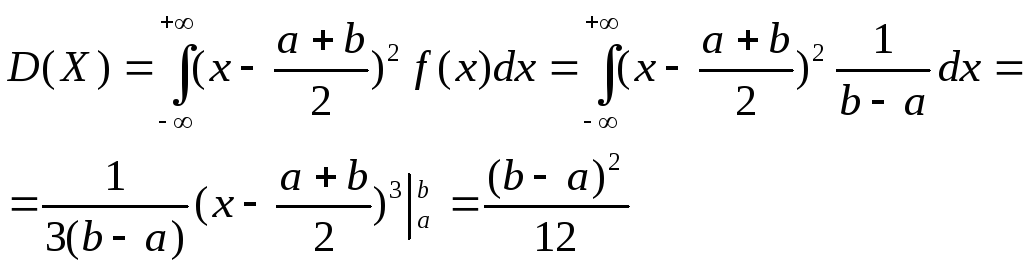
Следовательно,
![]() ,
,
![]() ,
,
![]()
Равномерный
закон распределения применяется при
работе с округленными числами. Например,
если число округлено до целого, то ошибка
округления
![]() распределена
равномерно на
распределена
равномерно на
![]() .
.
38. Показательный закон распределения
Непрерывная случайная величина X, которая принимает только неотрицательные значения с плотностью распределения
![]() ,
,
![]()
называется
распределенной по показательному закону
с параметром
![]() .
Так как
.
Так как
![]() ,
,
т.е. приведенное определение корректно.
Функция распределения показательно распределенной случайной величины X имеет вид:
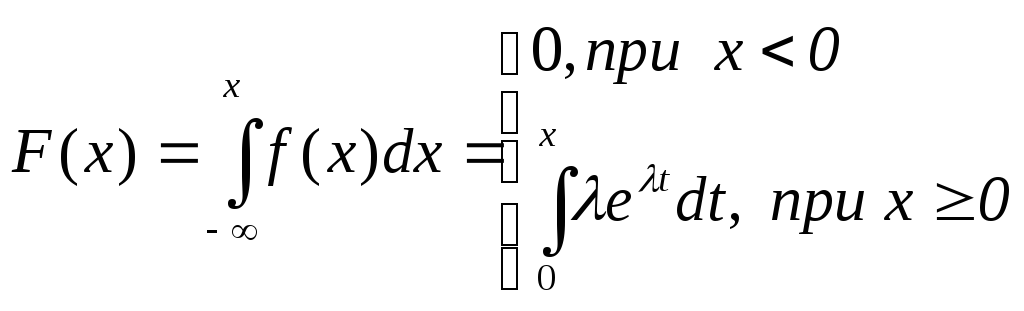
графики
Найдем математическое ожданиеи дисперсию случайной величины, распределенной по показательному закону.
![]()
![]()
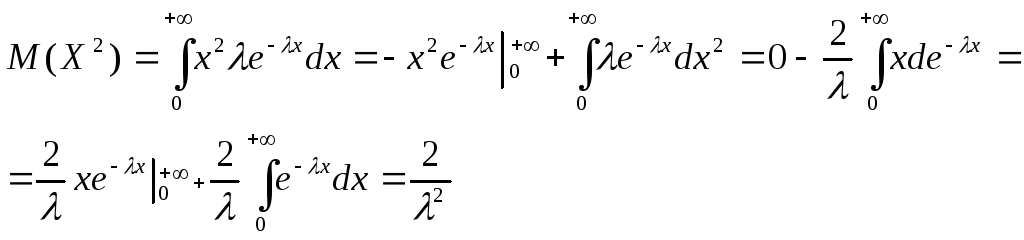
Поэтому
![]()
Пример. Среднее время обслуживания покупателя 20 минут. Чему равна вероятность простоя в очереди от 20 минут до 40 минут?
Решение.
Мат. ожидание
![]() .
Искомая вероятность
.
Искомая вероятность
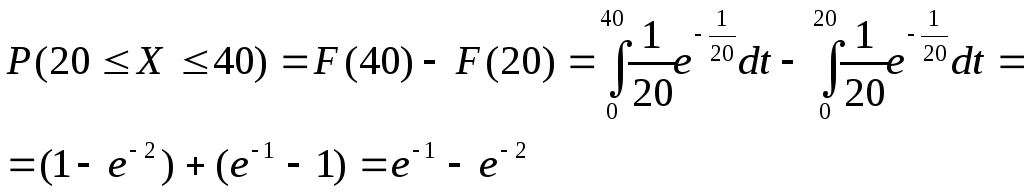
39. Нормальный закон распределения
Случайная величина X распределена по нормальному закону, если плотность рапределения определяется по формуле
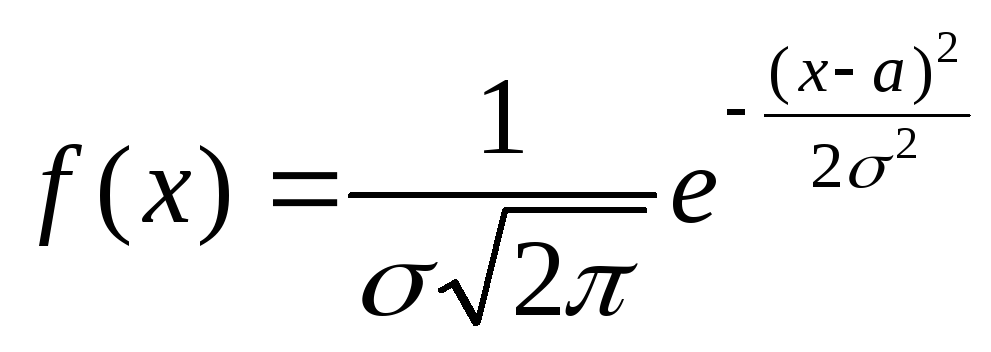
где
![]() и а
– параметры распределения.
и а
– параметры распределения.
Так
как
![]() и
и
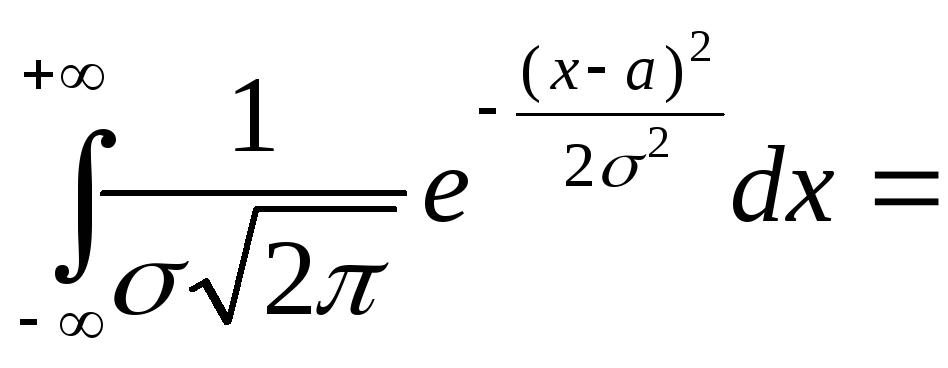 [введем замену
[введем замену
![]() ]
]
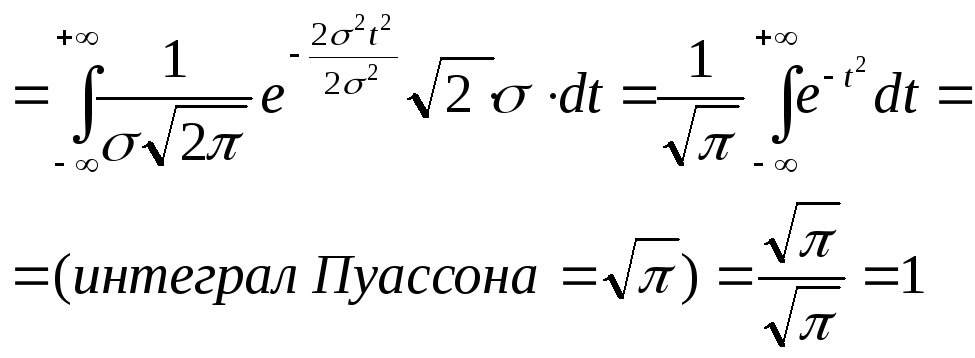
таким образом, приведенное выше определение корректно.
40. Математическое ожидание нормального закона распределения
Найдем
математическое ожидание случайной
величины X
, распределенной
по нормальному закону с параметрами
![]() и а:
и а:
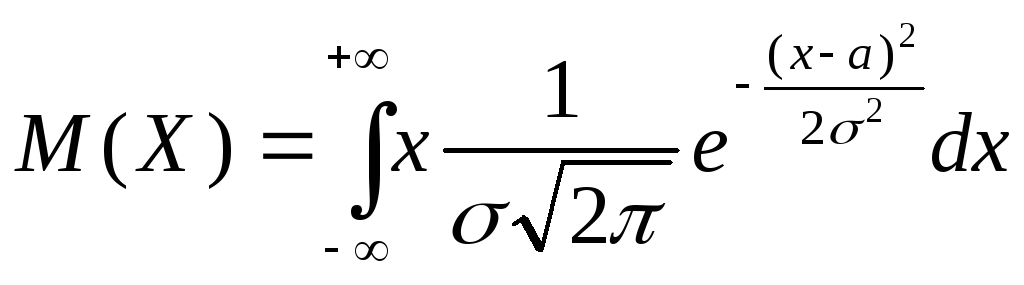
Проведем
замену в этом интеграле
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
пределы интегрирования не меняются и,
следовательно,
,
пределы интегрирования не меняются и,
следовательно,
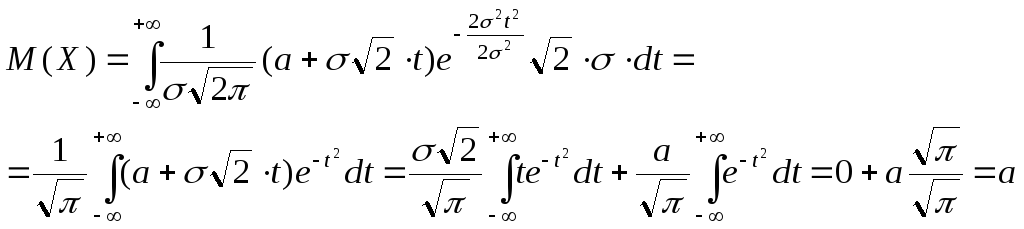
(интеграл от нечетной функции равен нулю по симметричному относительно начала координат промежутку).
