
- •1. Событие. Классификация событий
- •2. Вероятность события. Свойства вероятности. Классическая вероятность
- •3. Статистическое определение вероятности
- •4. Геометрическая вероятность
- •5. Задача о встрече
- •6. Действия над событиями
- •7. Теорема сложения вероятностей
- •8. Теорема умножения вероятностей
- •9. Условная вероятность события
- •10. Следствия из теоремы умножения вероятностей
- •11. Формула полной вероятности
- •12. Теорема гипотез. ( Формула Байеса )
- •13. Дискретные и непрерывные случайные величины
- •14. Закон распределения
- •15. Функция распределения
- •16. Общие свойства функции распределения
- •17. Плотность распределения
- •18. Основные свойства плотности распределения
- •19. Математическое ожидание и его свойства
- •20. Математическое ожидание непрерывной случайной величины
- •21. Мода и медиана
- •22. Дисперсия случайной величины
- •23. Свойства дисперсии
- •27. Условные законы распределения. Зависимые и независимые случайные величины
- •30. Корреляционный момент случайных величин и его свойства
- •31. Коэффициент корреляции и его свойства
- •32. Формула Бернулли
- •33. Наивероятнейшее число наступления события
- •34. Асимптотические формулы вычисления вероятностей
- •35. Биномиальный закон распределения
- •36. Закон распределения Пуассона
- •37. Равномерный закон распределения
- •38. Показательный закон распределения
- •39. Нормальный закон распределения
- •40. Математическое ожидание нормального закона распределения
- •41. Дисперсия нормального закона распределения
- •44. Неравенство Маркова
- •45. Неравенство Чебышева
- •46. Теорема Чебышева
- •47. Теорема Бернулли
- •48. Теорема Ляпунова
- •49. Интегральная теорема Лапласа
- •50. Виды статистических наблюдений
- •Виды статистических наблюдений:
- •51. Виды измерений
- •Количественные измерения
- •Порядковые (ранговые) измерения
- •Номинальные измерения
- •Статистические таблицы
- •52. Методы ранжирования
- •53. Группировка и табулирование количественных данных
- •54. Графическое изображение вариационных рядов
- •55. Показатели центра распределения (мода, медиана, среднее арифметическое, среднее гармоническое, среднее геометрическое)
- •56. Показатели вариации
- •57. Ассиметрия и эксцесс
- •58. Эмпирическая функция распределения
- •59. Точечные интервальные оценки
- •60. Доверительные интервалы
33. Наивероятнейшее число наступления события
Число
наступлений события
![]() ,
которому отвечает наибольшая вероятность,
называют наивероятнейшим
числом наступления
события
,
которому отвечает наибольшая вероятность,
называют наивероятнейшим
числом наступления
события
![]() .
.
Пусть
![]() - наивероятнейшее число наступлений
события
- наивероятнейшее число наступлений
события
![]() ,
тогда
,
тогда
![]() ,
,
![]() .
Отсюда
.
Отсюда
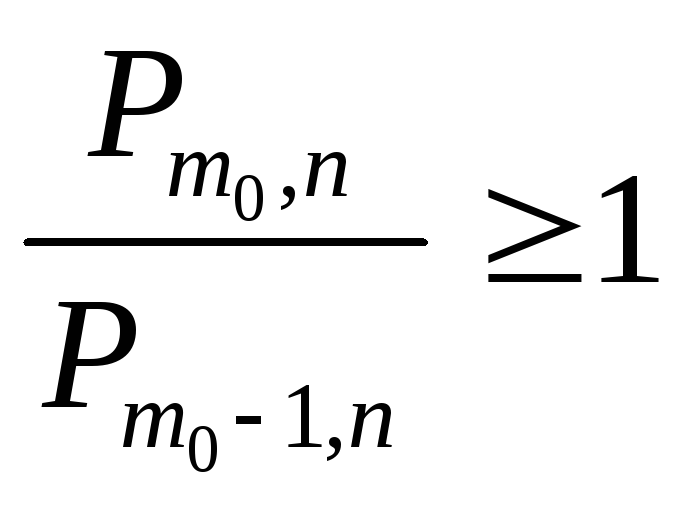 или
или
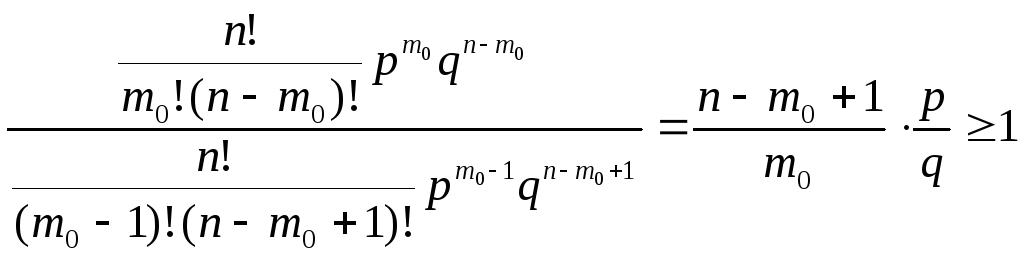 ,
следовательно,
,
следовательно,
![]() .
С другой стороны,
.
С другой стороны,
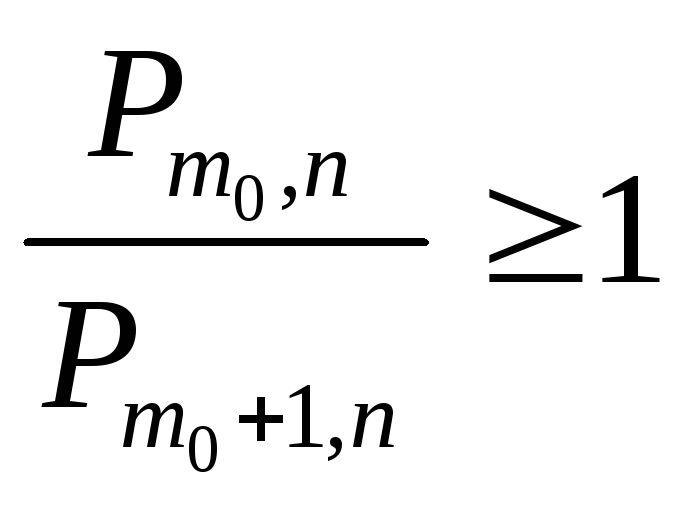 ,
тогда
,
тогда
![]() ,
т.е.
,
т.е.
![]() .
.
Итак,
![]() определяется двойным неравенством
определяется двойным неравенством
![]() .
Отметим, что разность
.
Отметим, что разность
![]() ,
следовательно, всегда существует целое
число
,
следовательно, всегда существует целое
число
![]() ,
удовлетворяющее двойному неравенству
выше. При этом если
,
удовлетворяющее двойному неравенству
выше. При этом если
![]() - целое число, то наивероятнейших чисел
будет два:
- целое число, то наивероятнейших чисел
будет два:
![]() и
и
![]() .
.
Пример 1. Доля изделий высшего сорта на данном предприятии составляет 31%. Чему равно наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий?
Решение.
В данном случае
![]() ,
,
![]() ,
,
![]() .
Составляем неравенство
.
Составляем неравенство
![]() или
или
![]() ,
следовательно,
,
следовательно,
![]() .
.
Пример 1. Сколько раз надо подбросить игральную кость, чтобы наивероятнейшее число выпадений «двойки» было равно 32?
Решение.
Здесь
![]() ,
,
![]() .
Требуется найти
.
Требуется найти
![]() -
число независимых испытаний. Воспользуемся
неравенством
-
число независимых испытаний. Воспользуемся
неравенством
![]() .
Откуда
.
Откуда
![]() и
и
![]() ,
получаем, что с одной стороны
,
получаем, что с одной стороны
![]() ,
а с другой -
,
а с другой -
![]() .
Таким образом, необходимо провести от
191 до 197 независимых испытаний.
.
Таким образом, необходимо провести от
191 до 197 независимых испытаний.
34. Асимптотические формулы вычисления вероятностей
При
больших
![]() и
и
![]() на
практике пользоваться формулой Бернулли
на
практике пользоваться формулой Бернулли
![]() затруднительно.
В этом случае
пользуются
локальной
теоремой Лапласа, которую приведем без
доказательства.
затруднительно.
В этом случае
пользуются
локальной
теоремой Лапласа, которую приведем без
доказательства.
Теорема.
Если вероятность
![]() наступления
события
наступления
события
![]() в каждом из
в каждом из
![]() испытаний отлична от 0 или 1, то
испытаний отлична от 0 или 1, то
![]() - вероятность
того, что
событие
- вероятность
того, что
событие
![]() при этом наступит
при этом наступит
![]() раз, при
раз, при
![]() удовлетворяет предельному неравенству
удовлетворяет предельному неравенству
![]() ,
,
где
![]() ,
,
![]() .
.
При
сделанных предположениях относительно
![]() ,
если
,
если
![]() достаточно большое, имеет место
приближенное равенство
достаточно большое, имеет место
приближенное равенство
![]() .
.
Пример. Вероятность изготовления детали высшего сорта на данном станке равна 0.4 . Найти вероятность того, что среди наудачу взятых 26 деталей половина окажется высшего сорта.
Решение.
Требуется найти вероятность
![]() ,
используя теорему Лапласа. Имеем
,
используя теорему Лапласа. Имеем
![]() =0.4
=0.4 ![]()
![]()
![]()
![]() =26
=26 ![]()
![]() =13
=13 ![]()
![]() ;
;
![]()
![]() .
.
Таким
образом, вероятность того, что среди
наудачу взятых 26 деталей половина
окажется высшего сорта, равна
![]() .
.
Формула
![]() эффективнее,
когда
эффективнее,
когда
![]() близко
к 0.5 . Если
близко
к 0.5 . Если
![]() - мало, пользуются асимптотической
формулой Пуассона, которая вытекает из
следующей теоремы Пуассона.
- мало, пользуются асимптотической
формулой Пуассона, которая вытекает из
следующей теоремы Пуассона.
Теорема.
Пусть
проводится
![]() независимых испытаний, в каждом из
которых событие
независимых испытаний, в каждом из
которых событие
![]() наступает с вероятностью
наступает с вероятностью
![]() .
Тогда, если число испытаний неограниченно
возрастает, а
.
Тогда, если число испытаний неограниченно
возрастает, а
![]() ,
причем
,
причем
![]() - величина постоянная, то
- величина постоянная, то
![]() .
.
35. Биномиальный закон распределения
Случайная
величина
![]() ,
которая принимает значение
,
которая принимает значение
![]() с вероятностью
с вероятностью
![]()
![]()
![]() ,
называется
распределенной по биномиальному закону.
,
называется
распределенной по биномиальному закону.
Если
проводятся независимые испытания, в
каждом из которых событие
![]() может наступить с одной и той же
вероятностью
может наступить с одной и той же
вероятностью
![]() ,
то число наступлений события
,
то число наступлений события
![]() в
в
![]() испытаниях и есть случайная величина
испытаниях и есть случайная величина
![]() .
.
Приведем таблицу распределения биномиальной случайной величины
|
Значения
|
0 |
1 |
2 |
… |
|
|
Вероятности |
|
|
|
… |
|
Проверим
корректность определения случайной
величины
![]() ,
т.е. выполнения требования
,
т.е. выполнения требования
![]() .
.
Здесь
![]() - вероятность того, что событие
- вероятность того, что событие
![]() не наступит ни разу;
не наступит ни разу;
![]() - наступит один раз;
- наступит один раз;
![]() - два раза и т.д. или, наконец,
- два раза и т.д. или, наконец,
![]() раз. Но это вероятность достоверного
события и поэтому равна единице.
раз. Но это вероятность достоверного
события и поэтому равна единице.
Найдем
математическое ожидание и дисперсию
биномиальной случайной величины
![]() .
Пусть
.
Пусть
![]() - это число наступлений события
- это число наступлений события
![]() в
в
![]() ом
испытании. Тогда распределение случайной
величины
ом
испытании. Тогда распределение случайной
величины
![]() задается таблицей
задается таблицей
|
Значения
|
0 |
1 |
|
Вероятности |
|
|
Очевидно,
что
![]() ,
,
![]() - независимые случайные величины и их
сумма
- независимые случайные величины и их
сумма
![]() - это случайная величина
- это случайная величина
![]() .
Найдем математическое ожидание и
дисперсию случайной величины
.
Найдем математическое ожидание и
дисперсию случайной величины
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Тогда
![]() ,
,
![]() .
.
Итак,
![]() ,
,
![]() ,
,
![]() .
.
