
- •1. Событие. Классификация событий
- •2. Вероятность события. Свойства вероятности. Классическая вероятность
- •3. Статистическое определение вероятности
- •4. Геометрическая вероятность
- •5. Задача о встрече
- •6. Действия над событиями
- •7. Теорема сложения вероятностей
- •8. Теорема умножения вероятностей
- •9. Условная вероятность события
- •10. Следствия из теоремы умножения вероятностей
- •11. Формула полной вероятности
- •12. Теорема гипотез. ( Формула Байеса )
- •13. Дискретные и непрерывные случайные величины
- •14. Закон распределения
- •15. Функция распределения
- •16. Общие свойства функции распределения
- •17. Плотность распределения
- •18. Основные свойства плотности распределения
- •19. Математическое ожидание и его свойства
- •20. Математическое ожидание непрерывной случайной величины
- •21. Мода и медиана
- •22. Дисперсия случайной величины
- •23. Свойства дисперсии
- •27. Условные законы распределения. Зависимые и независимые случайные величины
- •30. Корреляционный момент случайных величин и его свойства
- •31. Коэффициент корреляции и его свойства
- •32. Формула Бернулли
- •33. Наивероятнейшее число наступления события
- •34. Асимптотические формулы вычисления вероятностей
- •35. Биномиальный закон распределения
- •36. Закон распределения Пуассона
- •37. Равномерный закон распределения
- •38. Показательный закон распределения
- •39. Нормальный закон распределения
- •40. Математическое ожидание нормального закона распределения
- •41. Дисперсия нормального закона распределения
- •44. Неравенство Маркова
- •45. Неравенство Чебышева
- •46. Теорема Чебышева
- •47. Теорема Бернулли
- •48. Теорема Ляпунова
- •49. Интегральная теорема Лапласа
- •50. Виды статистических наблюдений
- •Виды статистических наблюдений:
- •51. Виды измерений
- •Количественные измерения
- •Порядковые (ранговые) измерения
- •Номинальные измерения
- •Статистические таблицы
- •52. Методы ранжирования
- •53. Группировка и табулирование количественных данных
- •54. Графическое изображение вариационных рядов
- •55. Показатели центра распределения (мода, медиана, среднее арифметическое, среднее гармоническое, среднее геометрическое)
- •56. Показатели вариации
- •57. Ассиметрия и эксцесс
- •58. Эмпирическая функция распределения
- •59. Точечные интервальные оценки
- •60. Доверительные интервалы
27. Условные законы распределения. Зависимые и независимые случайные величины
Пусть
у нас имеется случайный вектор
![]() ,
распределение которого дается таблицей:
,
распределение которого дается таблицей:
-
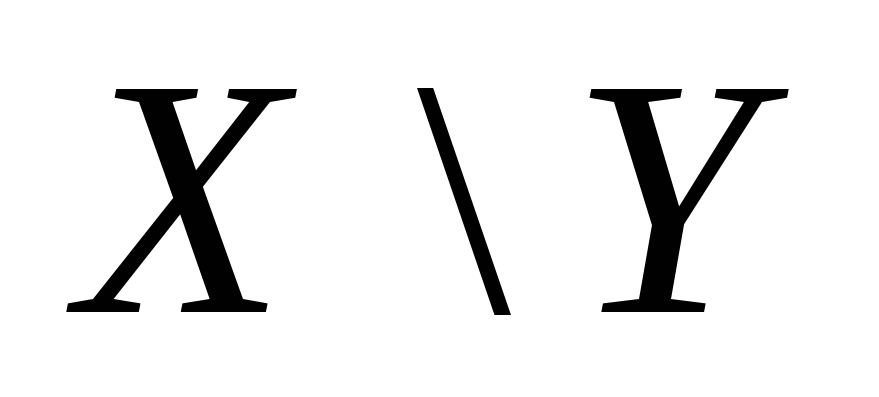
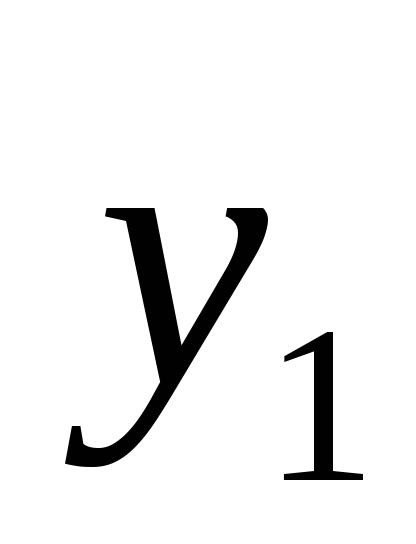
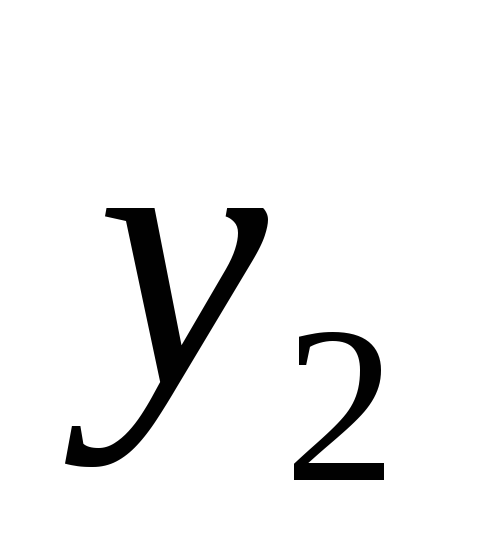

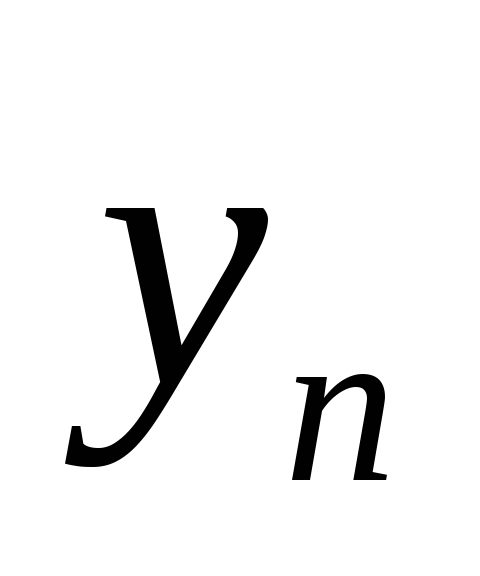
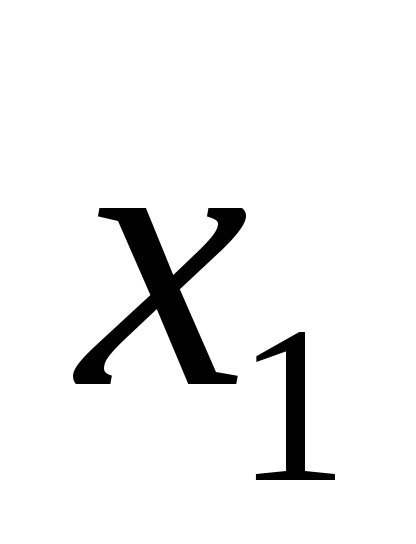

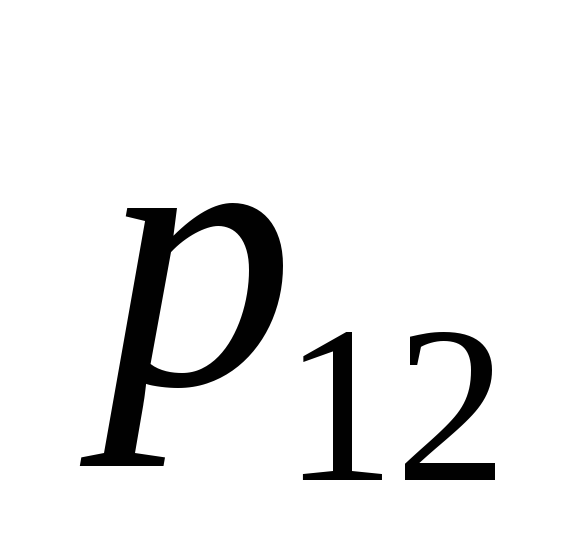

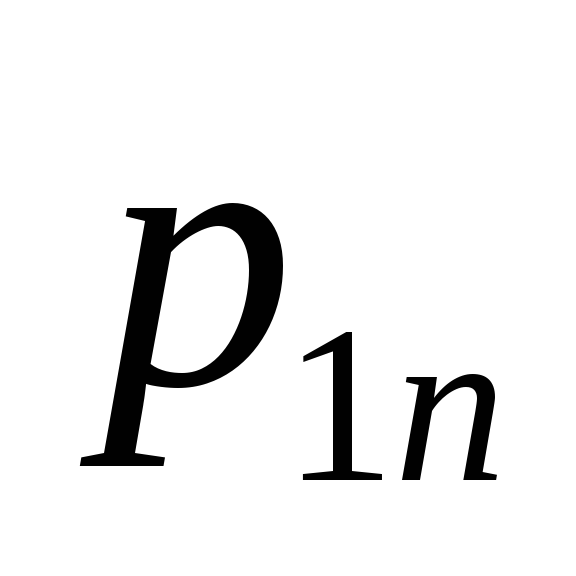
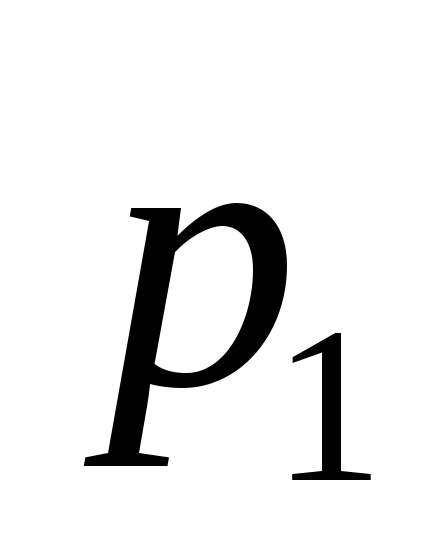
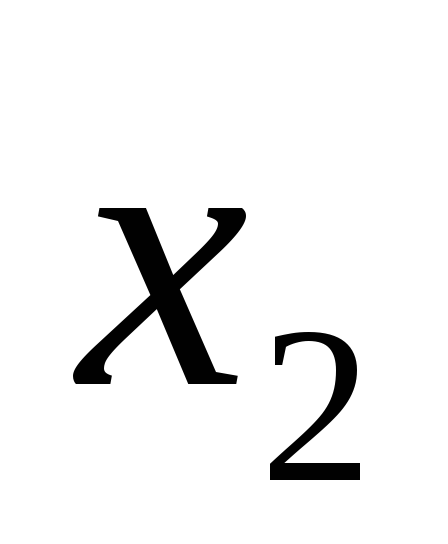
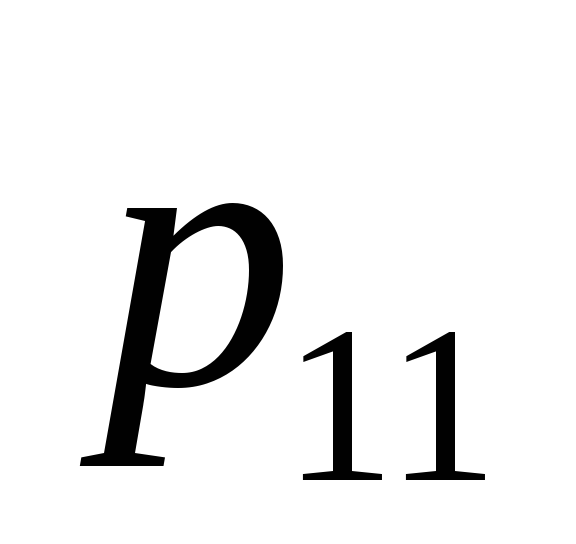
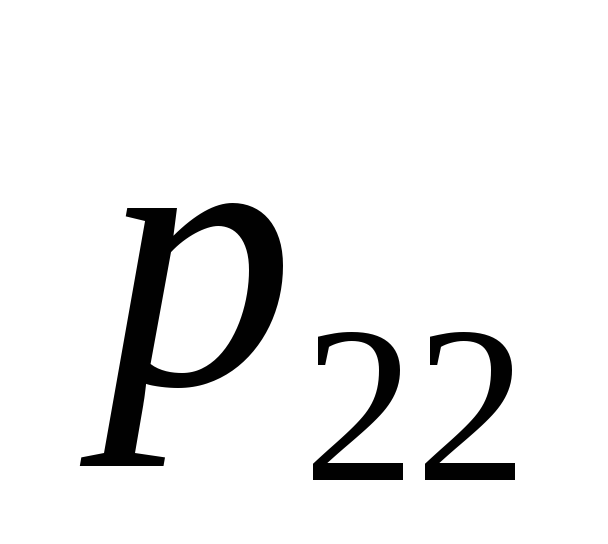

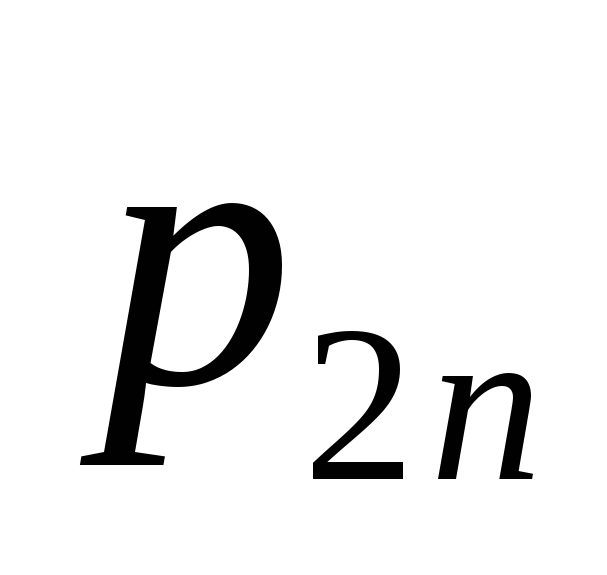
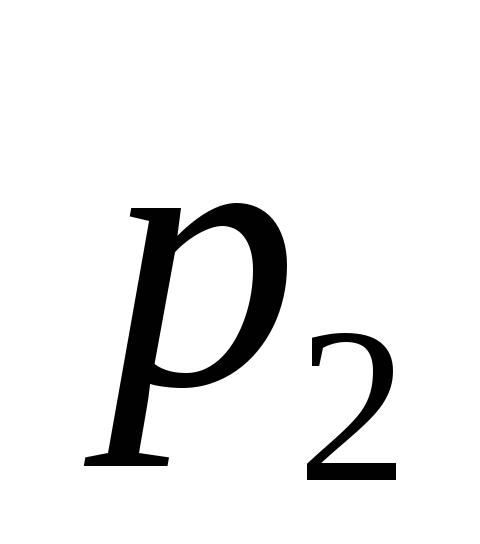






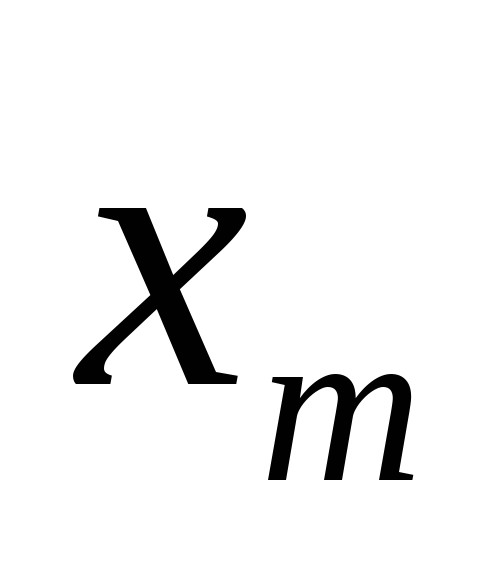
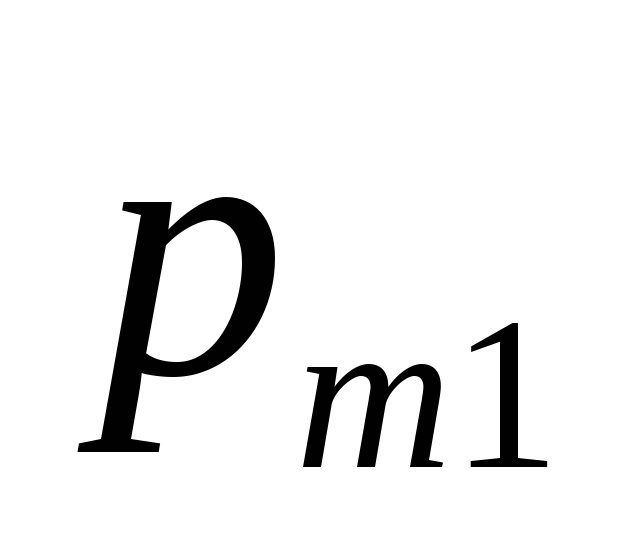


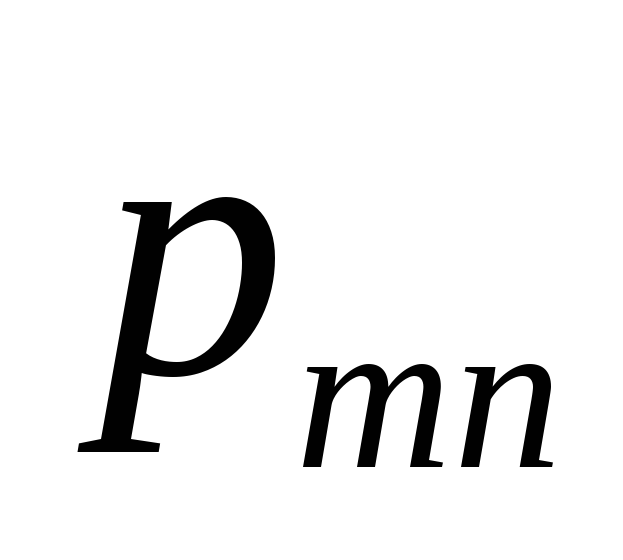
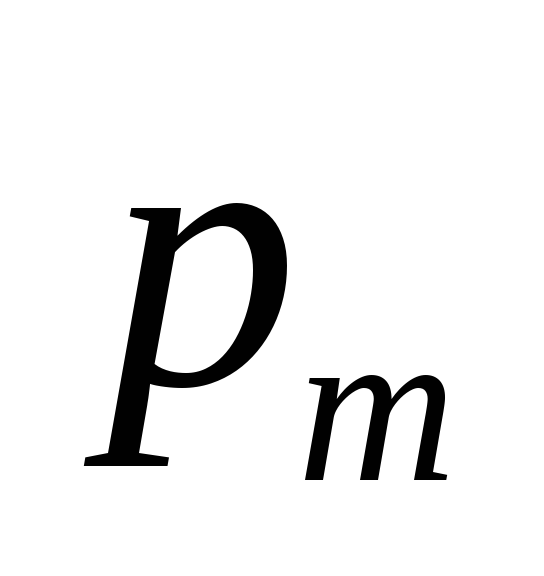

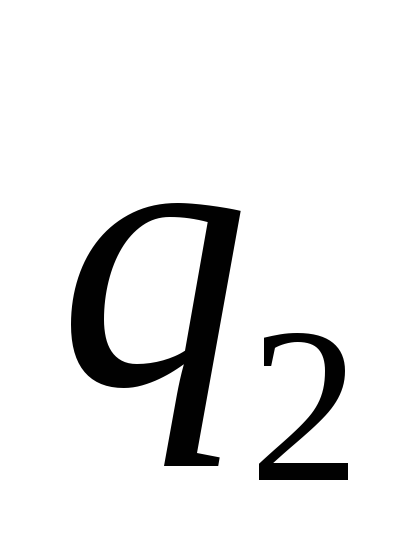

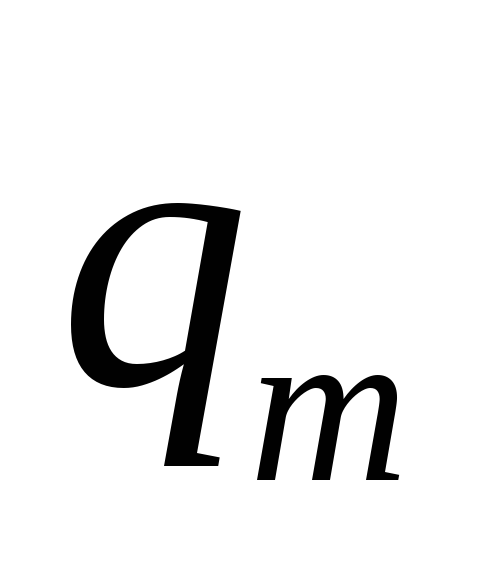
1
Рассмотрим
функцию распределения случайной величины
![]() при условии, что
при условии, что
![]() приняло значение
приняло значение
![]() ,
,
![]() .
Эту обозначают
.
Эту обозначают
![]() .
Найдем вероятность того, что
.
Найдем вероятность того, что
![]() приняло
значение
приняло
значение
![]() ,
когда
,
когда
![]() приняло
значение
приняло
значение
![]() :
:
![]()
![]() .
.
Аналогично
![]()
![]() .
.
В
случае непрерывного распределения
вектора
![]() появляются
условные плотности распределения
появляются
условные плотности распределения
![]() ,
когда
,
когда
![]() ,
и
,
и
![]() ,
когда
,
когда
![]() ,
то есть
,
то есть
![]() и
и
![]() .
Можно показать, что
.
Можно показать, что
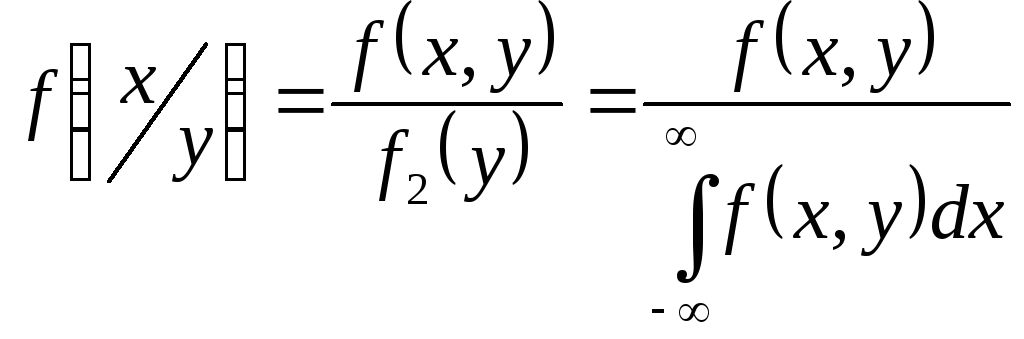

где
![]() – плотность распределения случайной
величины
– плотность распределения случайной
величины
![]() ,
а
,
а
![]() – плотность распределения У.
– плотность распределения У.
Случайная
величина
![]() называется независимой
от случайной величины
называется независимой
от случайной величины
![]() ,
если распределение
,
если распределение
![]() не зависит от того, какое значение
приняло
не зависит от того, какое значение
приняло
![]() .
Аналогично определяется независимость
.
Аналогично определяется независимость
![]() от
от
![]() .
Свойство независимости случайных
величин взаимно. Если величины
.
Свойство независимости случайных
величин взаимно. Если величины
![]() и
и
![]() независимы, то в этом случае
независимы, то в этом случае
![]() (дискретное распределение) и
(дискретное распределение) и
![]() (непрерывное
распределение).
(непрерывное
распределение).
Пример.
Для случайного вектора
![]() плотность
распределения:
плотность
распределения:
![]()
Найти
функцию распределения случайного
вектора
![]() ,
случайных величин
,
случайных величин
![]() и
и
![]() ,
условные плотности распределения.
,
условные плотности распределения.
Решение.
Сначала определим корректность задания
случайного вектора
![]() .
.
-
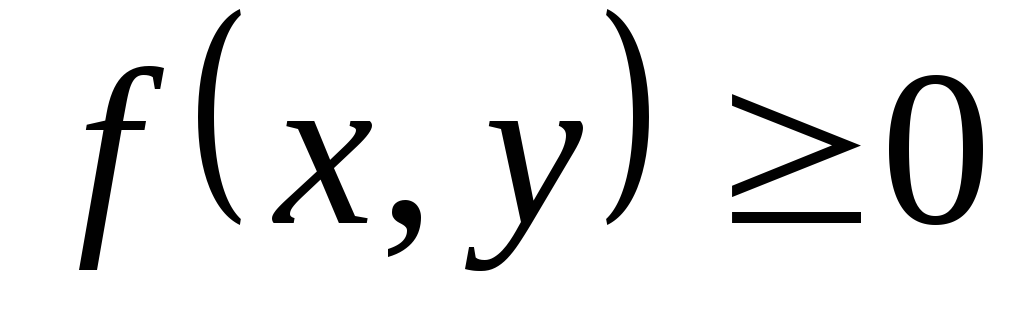 -
очевидно.
-
очевидно. -
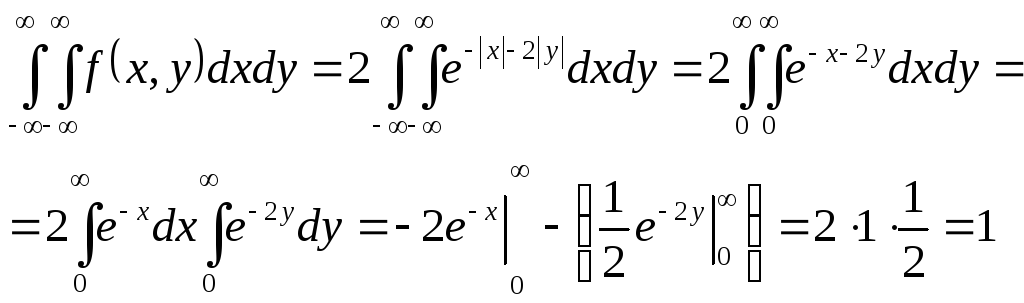
Найдем
функцию распределения данного случайного
вектора
![]() .
.
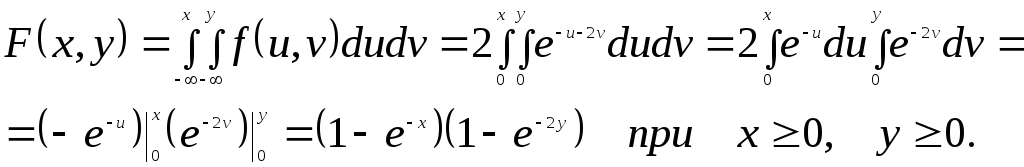
Для всех других точек
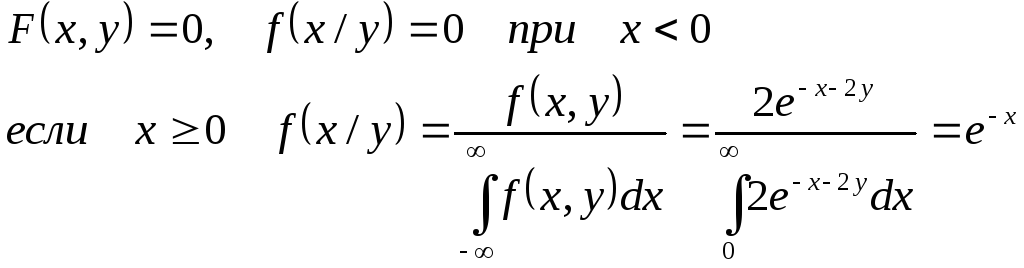
![]() при
при
![]()
![]() при
при
![]() .
.
Аналогично
![]() при
при
![]() и
и
![]() при
при
![]() .
.
Аналогично
![]() при
при
![]() и
и
![]() при
при
![]() .
.
Мы
видим, что в данном примере
![]() и
и
![]() - независимые величины.
- независимые величины.
28-29. Функция одной случайной величины
Пусть
дана функция одной переменной
![]() с областью определения
с областью определения
![]() и некоторая случайная величина
и некоторая случайная величина
![]() ,
все значения которой принадлежат
множеству
,
все значения которой принадлежат
множеству
![]() .
Тогда, если
.
Тогда, если
![]() приняла значение
приняла значение
![]() ,
будем считать, что новая случайная
величина
,
будем считать, что новая случайная
величина
![]() приняла значение
приняла значение
![]() .
Эта новая случайная величина называется
функцией
случайной величины
.
Эта новая случайная величина называется
функцией
случайной величины
![]() ,
и в этом случае пишут:
,
и в этом случае пишут:
![]() .
.
Вопрос
состоит в том, каков закон распределения
![]() ,
если мы знаем закон распределения
,
если мы знаем закон распределения
![]() .
.
Остановимся
сначала на дискретной случайной величине
![]() ,
закон распределения вероятностей
которой задается таблицей
,
закон распределения вероятностей
которой задается таблицей
|
|
|
|
|
|
|
|
|
|
|
|
Событие
![]() происходит с вероятностью
происходит с вероятностью
![]() ,
с этой же вероятностью
,
с этой же вероятностью
![]() примет значение
примет значение
![]() .
Мы имеем таблицу распределения
.
Мы имеем таблицу распределения
![]()
|
Значения
|
|
|
|
|
|
вероятности |
|
|
|
|
Если
существует несколько значений
![]() ,
для которых
,
для которых
![]() принимает одно и то же значение, то все
такие случаи объединяются в один,
которому соответствует по теореме
сложения вероятность, равная сумме
вероятностей объединяемых случаев.
принимает одно и то же значение, то все
такие случаи объединяются в один,
которому соответствует по теореме
сложения вероятность, равная сумме
вероятностей объединяемых случаев.
Пример.
Пусть распределение случайной величины
![]() задается следующим образом:
задается следующим образом:
|
|
-2 |
-1 |
0 |
1 |
2 |
|
|
0.1 |
0.1 |
0.3 |
0.3 |
0.2 |
Требуется
найти законы распределения случайных
величин
![]() и
и
![]() .
.
Решение.
Возможные значения
![]() :
:
![]() .
Отсюда
.
Отсюда
![]() принимает значения 0, 1, 4 соответственно
с вероятностями 0.3; 0.1+0.3=0.4; 0.1+0.2=0.3. Таким
образом, таблицей распределения
принимает значения 0, 1, 4 соответственно
с вероятностями 0.3; 0.1+0.3=0.4; 0.1+0.2=0.3. Таким
образом, таблицей распределения
![]() будет таблица вида
будет таблица вида
|
|
0 |
1 |
4 |
|
|
0.3 |
0.4 |
0.3 |
Так
как функция
![]() - взаимно однозначная, то различным
значениям
- взаимно однозначная, то различным
значениям
![]() отвечают различные значения
отвечают различные значения
![]() и, следовательно, таблицей распределения
этой случайной величины будет таблица
вида
и, следовательно, таблицей распределения
этой случайной величины будет таблица
вида
|
|
-8 |
-1 |
0 |
1 |
8 |
|
|
0.1 |
0.1 |
0.3 |
0.3 |
0.2 |
Теперь
остановимся на случае, когда
![]() - непрерывная случайная величина с
плотностью распределения
- непрерывная случайная величина с
плотностью распределения
![]() .
Пусть имеется монотонно возрастающая
на множестве значений случайной величины
.
Пусть имеется монотонно возрастающая
на множестве значений случайной величины
![]() функция
функция
![]() (
(![]() - непрерывно дифференцируемая и
- непрерывно дифференцируемая и
![]() ).
Если множество значений
).
Если множество значений
![]() и
и
![]() и
и
![]() ,то
функция распределения
,то
функция распределения
![]()
![]()
![]()



![]()
![]()





![]() 0
0
![]()
![]()
![]()
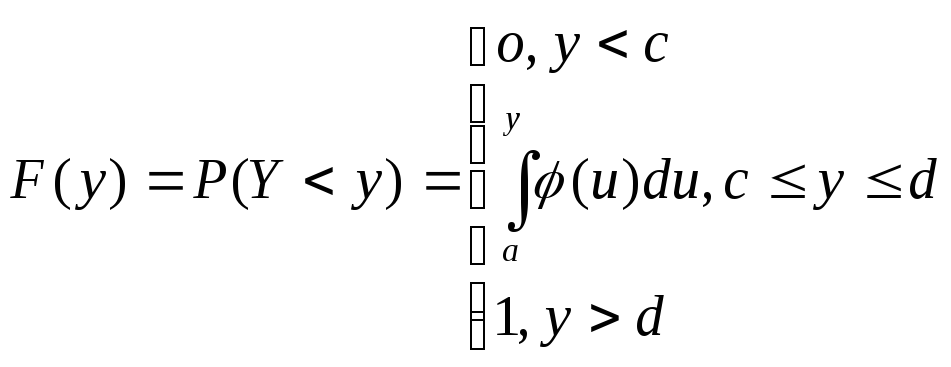 .
Здесь
.
Здесь
![]() – есть плотность распределения
– есть плотность распределения
![]() .
.
Для
![]()
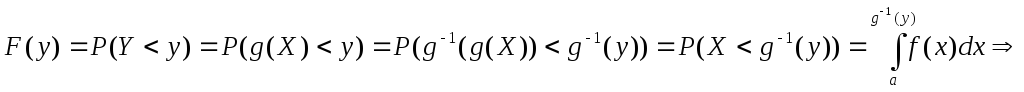
(![]() -
функция, обратная к
-
функция, обратная к
![]() на сегменте
на сегменте
![]() ).
Отсюда
).
Отсюда
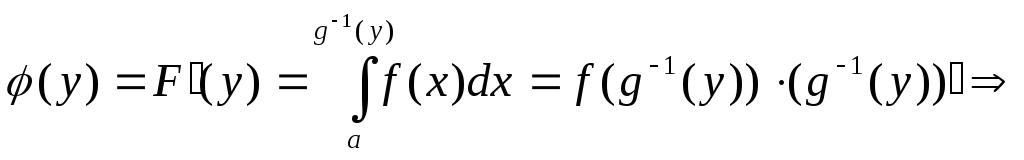
![]()
(мы воспользовались теоремой Барроу о производной от определенного интеграла с переменным верхним пределом по этому верхнему пределу).
Если
![]() - монотонно убывающая функция и
- монотонно убывающая функция и
![]() для всех
для всех
![]() из промежутка
из промежутка
![]() ,
то для
,
то для
![]() функция распределения имеет вид
функция распределения имеет вид
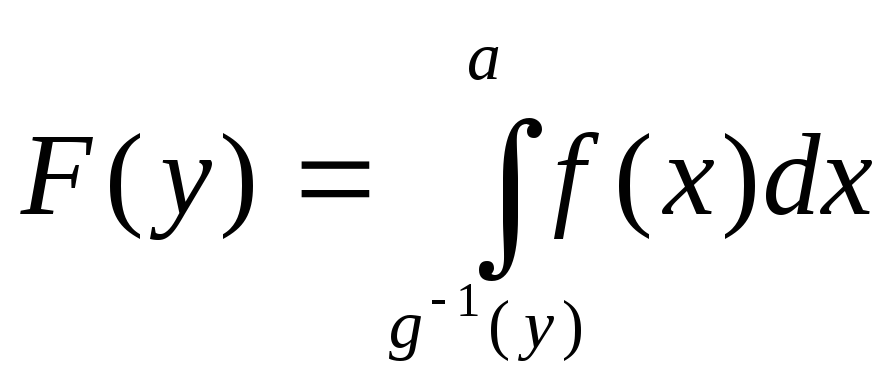 ,
,
а
плотность -
![]() ,
так как
,
так как
![]() - функция монотонно убывающая и ее
производная отрицательная.
- функция монотонно убывающая и ее
производная отрицательная.
Пример.
Пусть
![]() принимает значения только на сегменте
принимает значения только на сегменте
![]() с плотностью распределения
с плотностью распределения
![]() . Найти плотность распределения случайной
величины
. Найти плотность распределения случайной
величины
![]() .
.
Решение.
![]() –
функция монотонная возрастающая,
обратная к ней функция
–
функция монотонная возрастающая,
обратная к ней функция
![]() ,
а
,
а
![]() .
Поэтому, плотность распределения
.
Поэтому, плотность распределения
![]() будет
будет
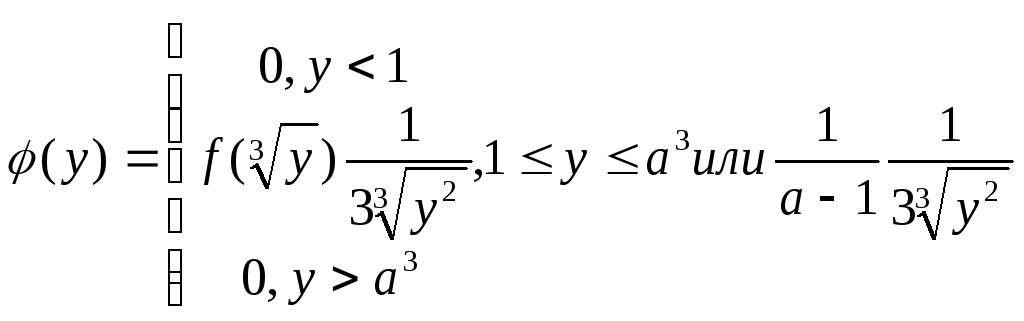
Пример.
Даны две независимые случайные величины:
![]() – число появлений герба при двух
подбрасываниях монеты и
– число появлений герба при двух
подбрасываниях монеты и
![]() – число очков, выпавших при подбрасывании
игральной кости. Найти закон распределения
разности
– число очков, выпавших при подбрасывании
игральной кости. Найти закон распределения
разности
![]() .
.
Решение.
Запишем законы распределения данных
случайных величин
![]() и
и
![]() .
.
|
|
0 |
1 |
4 |
|
|
|
|
|
и
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
Составим
таблицу распределения случайной величины
![]() ,
полагая
,
полагая
![]() .
.
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
… |
… |
|
|
|
|
… |
… |
|
|
|
… |
… |
… |
|
|
|
-1 |
-2 |
-3 |
-4 |
-5 |
-6 |
0 |
-1 |
-2 |
-3 |
-4 |
-5 |
1 |
0 |
-1 |
-2 |
-3 |
-4 |
Тогда
|
|
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
или
|
|
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
