Построение матрицы жёсткости
При перемножении следует учитывать, что данная операция не коммутативна, т.е. матрицы необходимо перемножать именно в том порядке, в котором они записаны.
Итоговая матрица жёсткости каждого элемента может быть представлена в виде
,
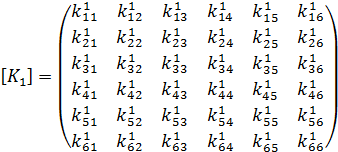где
верхний индекс обозначает номер конечного
элемента. Элементы справа и слева
относительно главной диагонали должны
быть одинаковы. Таким образом, левый
нижний угол должен быть зеркальным
отражением верхнего правого с осью
симметрии, проходящей через главную
диагональ (
)
Так можно проверить правильность
построения матрицы.
Данным матрицам соответствуют перемещения узлов, принадлежащих первому и второму конечным элементам.
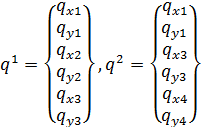
10
6.Вычисления
Дано: a = 0,1 м; b = 0,5 м; h = 0,002 м; E = 2·1011 Па; µ = 0,33;
;
=
20000 Н;
Вектора перемещений (2) и нагрузок (3) выглядят следующим образом
,
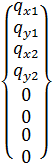Площади КЭ S1 = S2 = 0,0125 м2.
Координаты узлов (5)
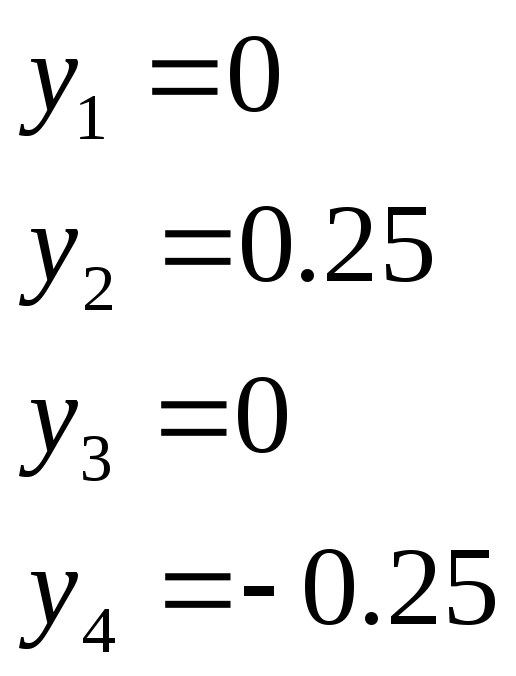
Матрицы [B1] (6) и [B2] (7).
|
10 |
0 |
0 |
0 |
-10 |
0 |
|
0 |
-4 |
0 |
4 |
0 |
0 |
|
-4 |
10 |
4 |
0 |
0 |
-10 |
|
-10 |
0 |
0 |
0 |
10 |
0 |
|
0 |
0 |
0 |
-4 |
0 |
4 |
|
0 |
-10 |
-4 |
0 |
4 |
10 |
11
Транспонируем матрицы B1 и B2.
-
-10
0
-4
0
-4
10
0
0
4
0
4
0
-10
0
0
0
0
-10
|
-10 |
0 |
0 |
|
0 |
0 |
-10 |
|
0 |
0 |
-4 |
|
0 |
-4 |
0 |
|
10 |
0 |
4 |
|
0 |
4 |
10 |
Тогда матрицы жесткостей конечных элементов запишутся в виде
-
-1059840000
-2400000
-60160000
-148000000
1120000000
150400000
-298400000
555200000
150400000
-179200000
148000000
-376000000
-60160000
150400000
60160000
0
0
-150400000
148000000
-179200000
0
179200000
-148000000
0
-1120000000
148000000
0
-148000000
1120000000
0
150400000
-376000000
-150400000
0
0
376000000
|
1120000000 |
0 |
0 |
148000000 |
-1120000000 |
-148000000 |
|
0 |
376000000 |
150400000 |
0 |
-150400000 |
-376000000 |
|
0 |
150400000 |
60160000 |
0 |
-60160000 |
-150400000 |
|
148000000 |
0 |
0 |
179200000 |
-148000000 |
-179200000 |
|
-1120000000 |
-150400000 |
-60160000 |
-148000000 |
1180160000 |
298400000 |
|
-148000000 |
-376000000 |
-150400000 |
-179200000 |
298400000 |
555200000 |
Общая матрица жёсткости системы выглядит следующим образом
|
60160000 |
-2400000 |
-60160000 |
-148000000 |
1120000000 |
298400000 |
-1120000000 |
-148000000 |
|
-298400000 |
931200000 |
150400000 |
-179200000 |
298400000 |
-376000000 |
-150400000 |
-376000000 |
|
-60160000 |
150400000 |
60160000 |
0 |
0 |
-150400000 |
0 |
0 |
|
148000000 |
-179200000 |
0 |
179200000 |
-148000000 |
0 |
0 |
0 |
|
-1120000000 |
298400000 |
0 |
-148000000 |
1180160000 |
0 |
-60160000 |
-150400000 |
|
298400000 |
-376000000 |
-150400000 |
0 |
0 |
555200000 |
-148000000 |
-179200000 |
|
-1120000000 |
-150400000 |
0 |
0 |
-60160000 |
-148000000 |
1180160000 |
298400000 |
|
-148000000 |
-376000000 |
0 |
0 |
-150400000 |
-179200000 |
298400000 |
555200000 |
Поскольку перемещения узлов №3и №4 равны нулю, перемещения узлов №1 и №2 определим из четырёх нижних строк разрешающей системы уравнений. Запишем
12
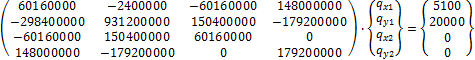
Решив данную систему методом Крамера, найдём корни уравнения.
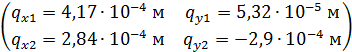
Найдём реакции в узлах №3 и №4, подставив определенные ранее значения перемещений узлов в разрешающую систему уравнений.
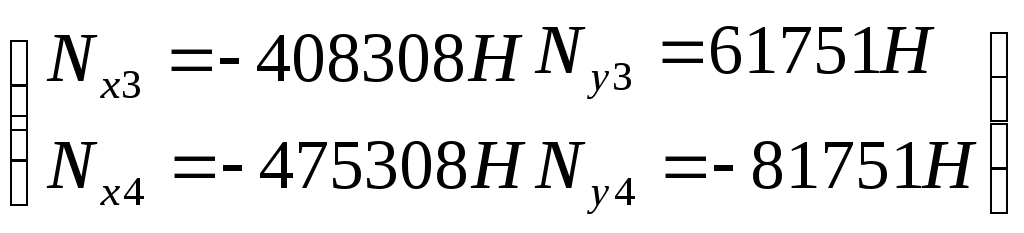
13