4.Условные обозначения

E – модуль жёсткости материала

D – матрица коэффициентов

В – матрица разности координат узлов

К – матрица жёсткости

q – матрица перемещений

4

Описание системы

Рассмотрим систему, состоящую из двух треугольных трёхузловых плоских конечных элементов, как показано на рис. 1.

Данная система представляет собой прямоугольник, стороны которого имеют размеры a (линия 1-3) и b (линии 2-4), толщиной h.

Пусть глобальная система координат, в которой будут производиться все расчёты, находится в узле №1. Всего данная система имеет восемь степеней свободы: перемещения вдоль осей х и y в каждом из узлов. Обозначим их q_ji, где j – ось перемещения, i – номер узла

6

Задание граничных условий

Зададим жёсткую заделку в верхней правой части четырехугольника (вдоль линии 3-4). Тогда перемещения в узлах №3 и №4 отсутствуют, т.е. q_x3 = q_y3 = q_x4 = q_y4 = 0. Однако при этом в узлах №3 и №4 будут действовать неизвестные реакции N_x3, N_y3, N_x4, N_y4.

На систему также действуют внешние силы. В узле №1 действует направленная вверх сила P_у1, а вдоль линии 1-4 приложена равномерная погонная нагрузка p₁₄ ( нагрузка вдоль линии имеет размерность Н/м).

Для дальнейшего расчёта погонную нагрузку необходимо привести к узлам. В силу её равномерности, она распределяется поровну между узлами, и приведение можно выполнить по следующей зависимости:

Для расчёта потребуются модуль жёсткости материала (параметры даны для стали) Па и коэффициент Пуассона µ = 0,33.

7

Построение векторов перемещений и сил

Вектора перемещений и глобальных реакций всех узлов будут записаны в виде:

,

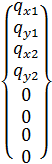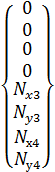
Тогда, общий вектор нагрузок, приходящихся на узлы

Построение матриц жесткостей отдельных элементов

Построим матрицу жёсткости на основе энергетического метода. Определим площадь каждого конечного элемента S_k. В данном случае S₁ = S₂ = a·b/2.

Далее найдём значения коэффициентов матрицы [D]

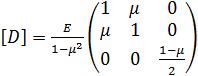(4)

Данная матрица одинакова для всех элементов, и все её коэффициенты являются константами. Она выведена из обобщённого закона Гука.

На следующем шаге решения найдём значения коэффициентов матриц [B₁] и [B₂], которые определяют связь геометрических характеристик внутри конечных элементов, вследствие чего для каждого элемента существует уникальная матрица [B]. Она состоит из разности координат узлов, входящих в конечный элемент. Запишем координаты узлов

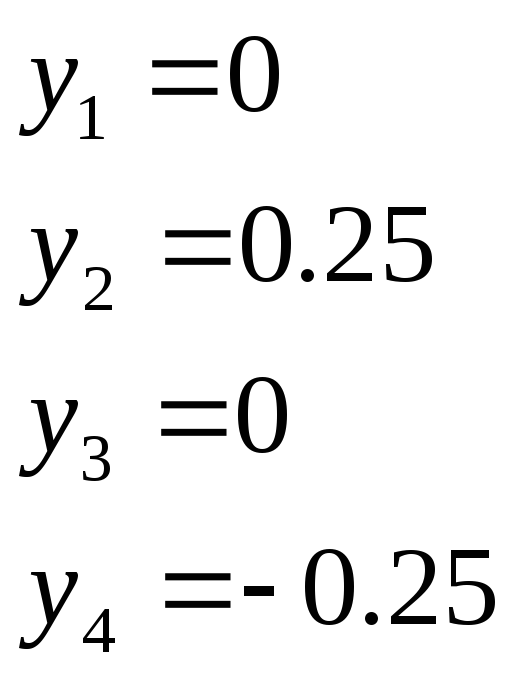
8

Тогда матрицы [B] для обоих конечных элементов запишутся в виде

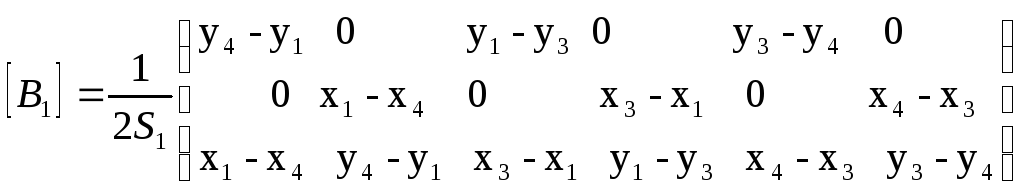
9