5. Линейные разностные уравнения с постоянными параметрами, их практическое значение и решение.

В общем случае линейное разностное уравнение с постоянными коэффициентами, относящееся к физически реализуемой системе, имеет следующий вид:

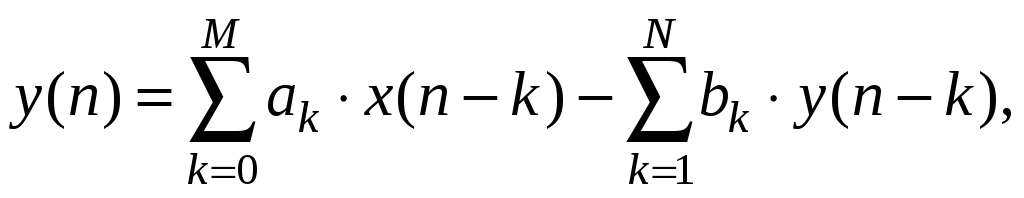
(1.27)

где коэффициенты и являются постоянными величинами и характеризуют конкретную систему.

Разностные уравнения для линейных дискретных систем играют ту же роль, что и дифференциальные уравнения для линейных аналоговых систем.

Как уже отмечалось, разностные уравнения позволяют определить способ построения соответствующей цифровой системы. Так, например, разностное уравнение первого порядка самого общего вида

(1.28)

можно реализовать с помощью следующей схемы (рис. 1.14). Здесь

Рис. 1.13. Реализация линейной дискретной системы первого порядка

блок «задержка» осуществляет задержку последовательностей x(n) и y(n) на один отсчёт.

Разностное уравнение второго порядка общего вида

(1.29)

реализуется схемой, представленной на рисунке 1.15.

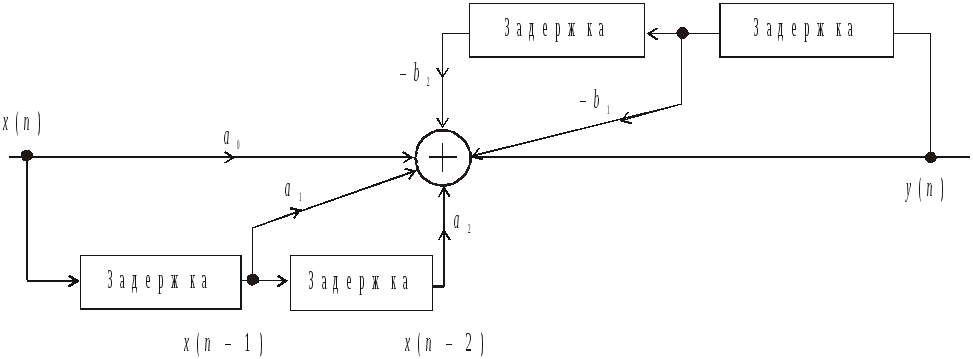
Рис. 1.14. Реализация линейной дискретной системы второго порядка

Очевидно, что рассмотренные системы первого и второго порядка могут быть использованы при реализации систем более высокого порядка путём последовательного или параллельного их соединения.

Наиболее подходящим способом решения линейных разностных уравнений является z-преобразование, которое позволяет заменить их решение решением алгебраических уравнений. Применение z-преобразо­вания к разностным уравнениям аналогично применению преобразования Лапласа к дифференциальным уравнениям.

6. Z-преобразование и его основные свойства. Связь с преобразованием Фурье.

В общем случае z-преобразование X(z) последовательности x(n) определяется следующим образом:

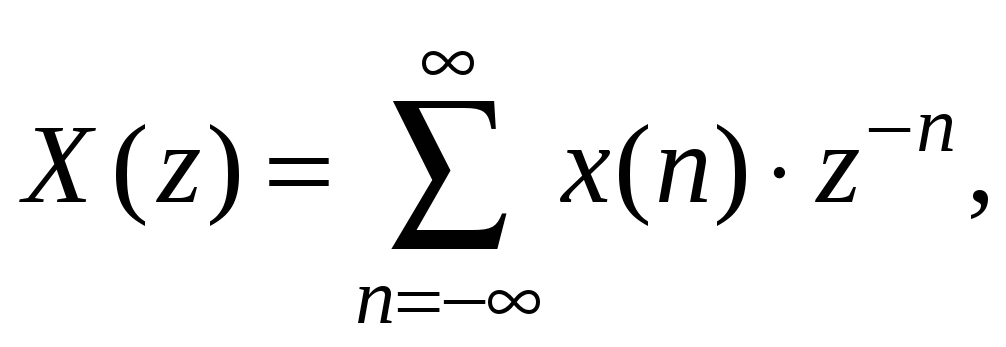(1.30)

где z – комплексная переменная.

Функция X(z) определяется для тех значений z или z^–1, для которых ряд в правой части выражения сходится. В этой связи следует отметить, что z-преобразование сходится не для всех последовательностей и не для всех значений z.

Представляя z в экспоненциальной форме

(1.31)

из исходного выражения для z-преобразования получим:

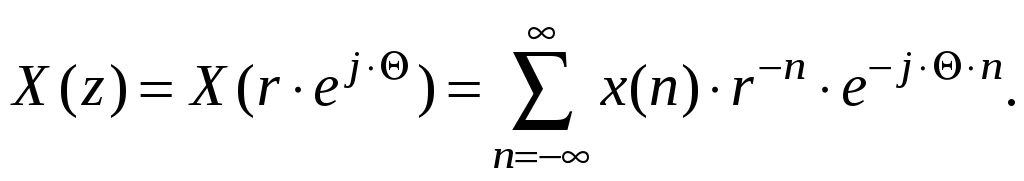(1.32)

Из теории функций комплексной переменной известно, что функция X(z) определяется для тех значений z в z-плоскости, для которых

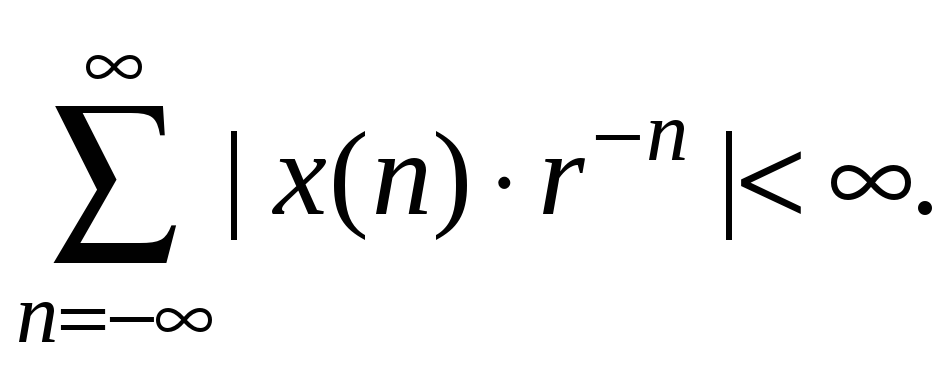(1.33)

Другими словами, исходная последовательность x(n) должна быть абсолютно суммируема.

Все значения z, для которых выполняется данное условие, образуют область сходимости z-преобразования и в этой области значения X(z) конечны. Область сходимости z-преобразования, физически реализуемой последовательности x(n), для которой для расположена вне определённого круга радиуса R в z-плоскости. Значение R зависит от расположения полюсов функции X(z) [полюс (нуль) функции X(z) расположен в точке z, где ]. Область сходимости можно также определить и в z^–1- плоскости. В этом случае для физически реализуемой последовательности область сходимости z-преобра­зования расположена внутри определённого круга с радиусом

Пример 1.1. Найти z-преобразование и область сходимости знакопостоянной экспоненциальной последовательности

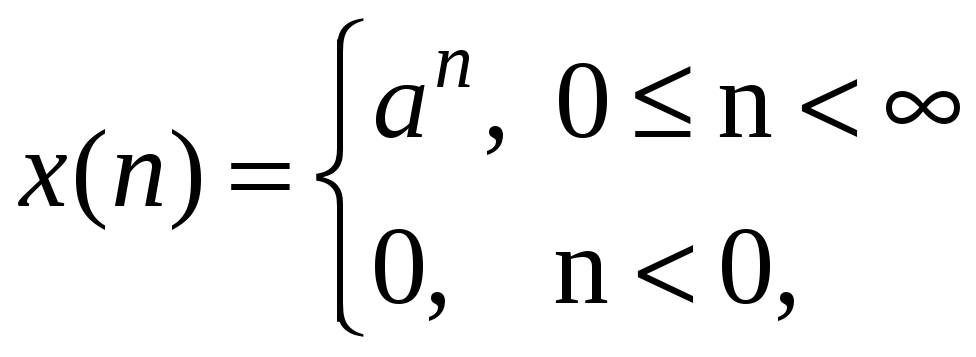
где

Решение. По определению имеем:

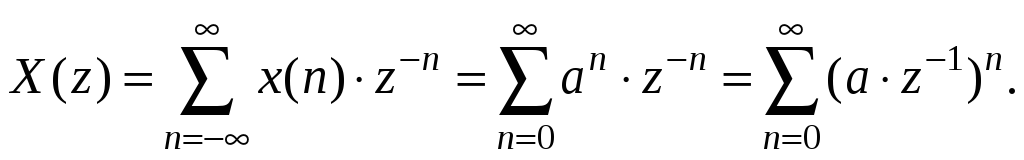
Полученное выражение представляет собой сумму членов бесконечно убывающей геометрической прогрессии, которая определяется по формуле:

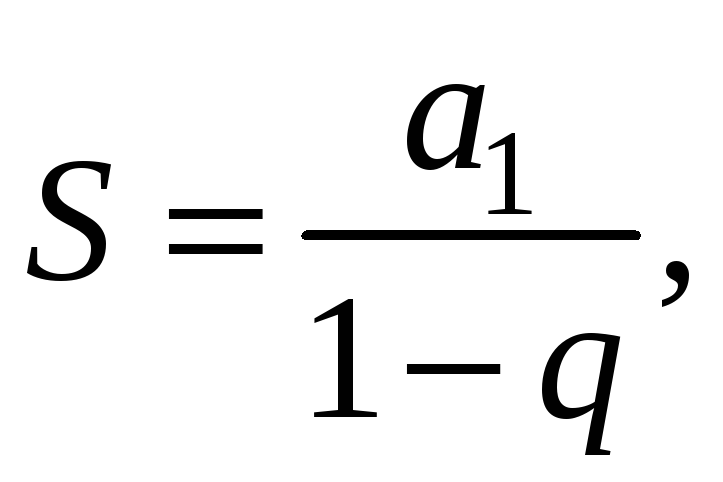
где в данном случае а знаменатель

Таким образом,

Для определения области сходимости воспользуемся результатами, полученными выше.

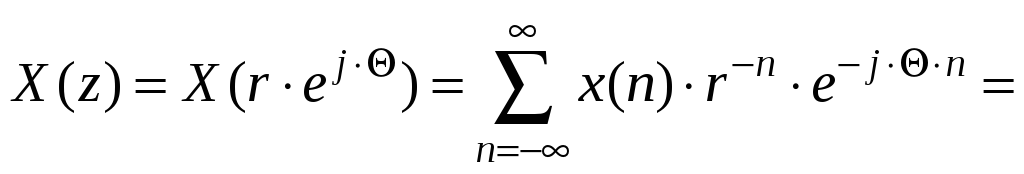
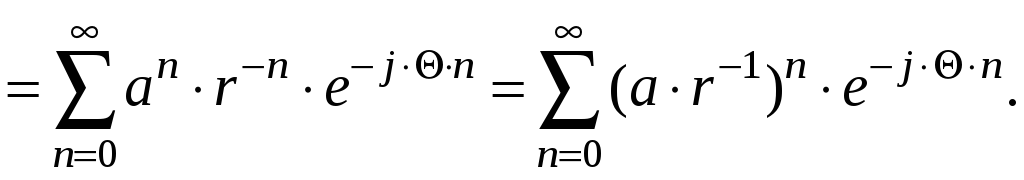
Отсюда следует, что областью сходимости являются те значения z, для которых

Очевидно, что это условие выполняется тогда и только тогда, когда

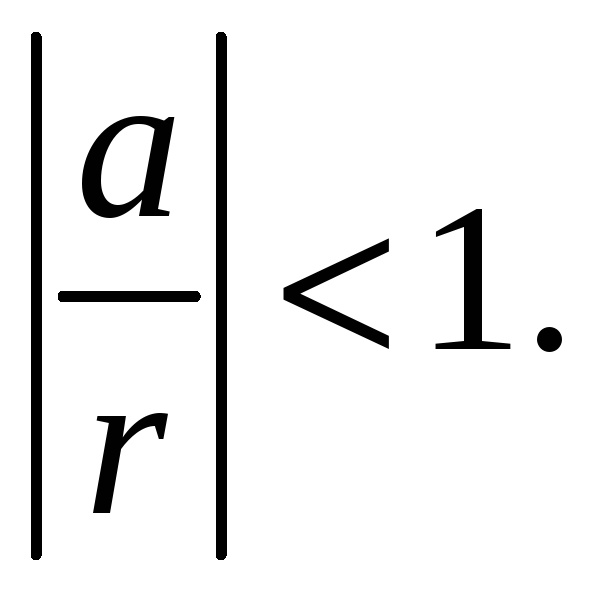
Следовательно, область сходимости последовательности в данном случае представляет собой часть z-плоскости вне круга радиуса как показано на рисунке 1.15.

Из выражения для X(z) видно, что полюс X(z) расположен в точке которая является границей области сходимости. Из последнего выражения видно также, что область сходимости X(z) в z^–1-плоскости лежит внутри круга с радиусом

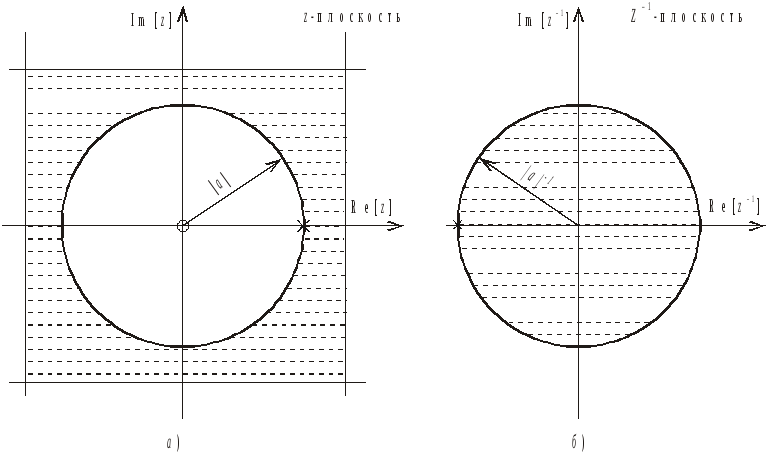
Рис. 1.16. Область сходимости экспоненциальной последовательности а) в z-плоскости; б) в z^–1-плоскости

Рассмотрим основные свойства z-преобразования.

1. Линейность. Если функции и есть z-преобразование последовательностей и соответственно, то для последовательности где a и b – произвольные постоянные, z-преобразование определяется таким образом:

(1.34)

2. Умножение на константу. Если X(z) есть z-преобразование X(n), то z-преобразование последовательности

где a – произвольная постоянная, определяется так:

(1.35)

3. Умножение на экспоненциальную последовательность. Если имеет z-преобразование X(z), то z-преобразование последовательности будет определяться как

(1.36)

4. Умножение на n(дифференцирование). Если x(n) имеет z-преоб­разование X(z), то последовательность будет иметь z-пре­образование

(1.37)

Это свойство полезно для вычисления обратного z -преобразования, когда X(z) содержит полюсы высокого порядка.

5. Сдвиг (задержка). Если последовательность имеет z-преоб­разование то для последовательности z-пре­обра­зование представляется в виде

(1.38)

Множитель является оператором задержки дискретной последова­тельности x(n) на m тактов (отсчетов) для любого m.

6. Свёртка. Если и есть z-преобразование последовательностей и соответственно, то для последовательности x(n), являющейся их свёрткой, т. е.

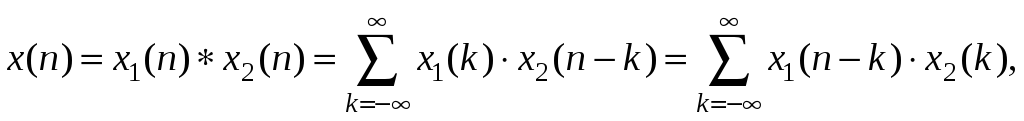
z-преобразование определяется в виде произведения z-преобразований и

(1.39)

7. Задержка физически реализуемых последовательностей. Односто­роннее z-преобразование. Свойства опережающего сдвига (упреждения).

При решении большинства практических задач обычно имеют дело с физически реализуемыми последовательностями, для которых вводится так называемое «одностороннее» z-преобразование:

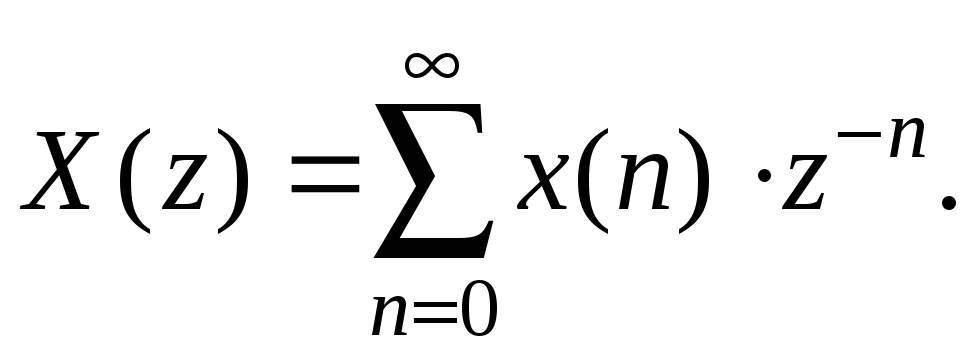(1.40)

При этом предполагается, что поведение последовательности x(n) до значения n = 0 неизвестно и его можно не учитывать. Для большинства таких последовательностей свойства одностороннего z-преобразования аналогичны свойствам обычного z-преобразования. Исключением является свойство сдвига (задержки). Рассмотрим последовательность с односторонним z-преобразованием и задержанную последовательность Одностороннее z-преобразование равно

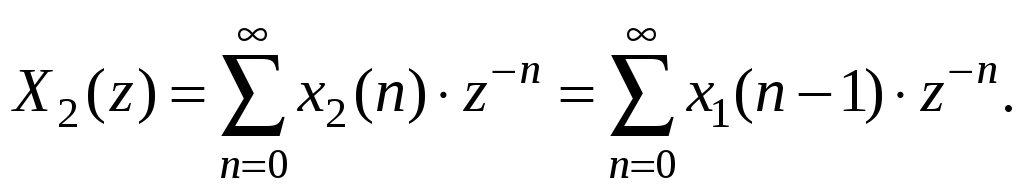
Обозначим тогда

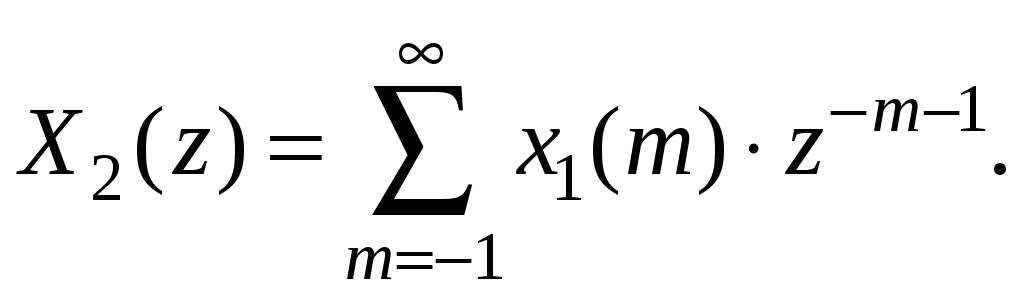
Последнее выражение можно переписать следующим образом:

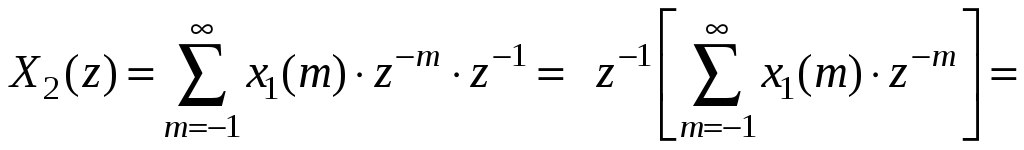
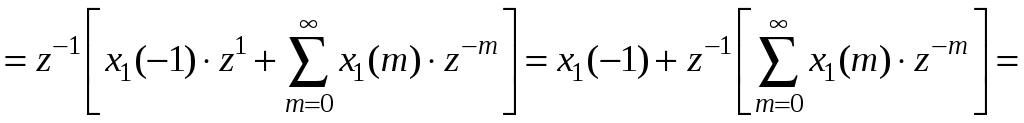
(1.41)

Как видно, задержка на один отсчёт по-прежнему приводит к умножению одностороннего z-преобразования на но при этом необходимо учесть значения последовательности при т. е. в этом случае важную роль начинают играть начальные условия.

Продолжая таким образом рассуждения дальше, можно получить, что z-преобразование последовательности будет определять­ся таким образом:

(1.42)

Для случая задержки последовательности на произвольное число отсчётов можно получить следующую формулу:

(1.43)

где

8. Свойство сопряжения. Если X(z) есть z-преобразование комплексной последовательности z-преобразование последовательностей и будут соответственно равны:

и (1.44)

9. Обращение времени. Если X(z) есть z-преобразование последовательности x(n), z-преобразование последовательности x₁(n)= x(–n) будет определяться таким образом:

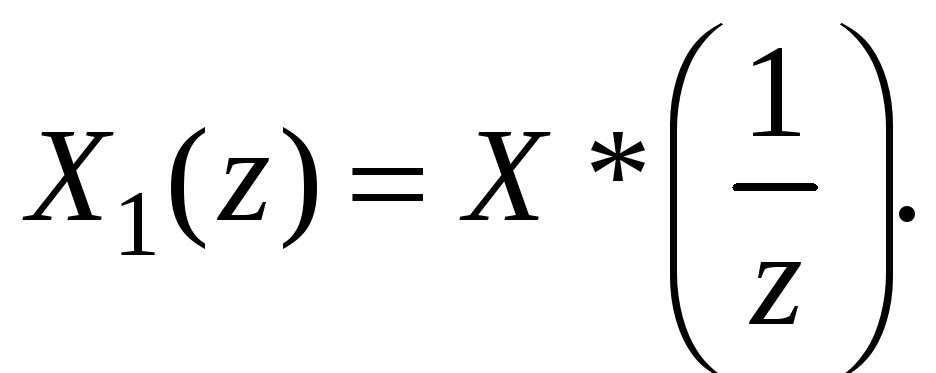(1.45)

Для последовательности x₂(n)= x*(–n) будет иметь

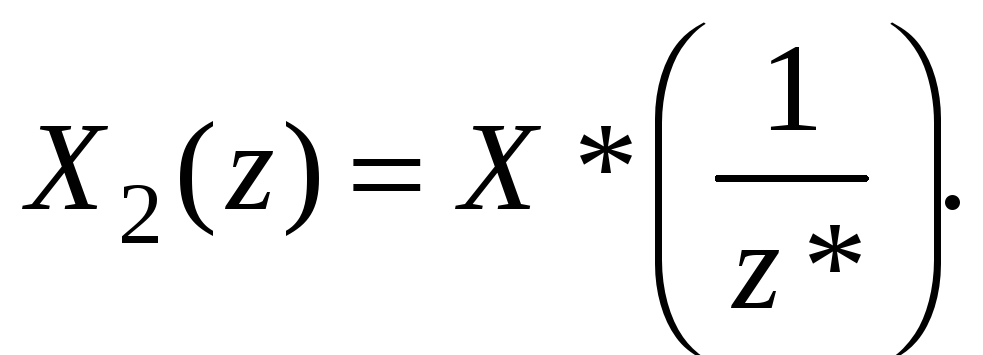(1.46)

10. Теорема о начальном значении. Если последовательность для всех n < 0 (т. е. она является физически реализуемой), а ее z-преобразование есть X(z), то

(1.47)

Z-преобразование последовательности можно рассматривать как способ ее однозначного представления в комплексной z-плоскости. Вычислим Z-преобразование последовательности x(n) при Из равенства

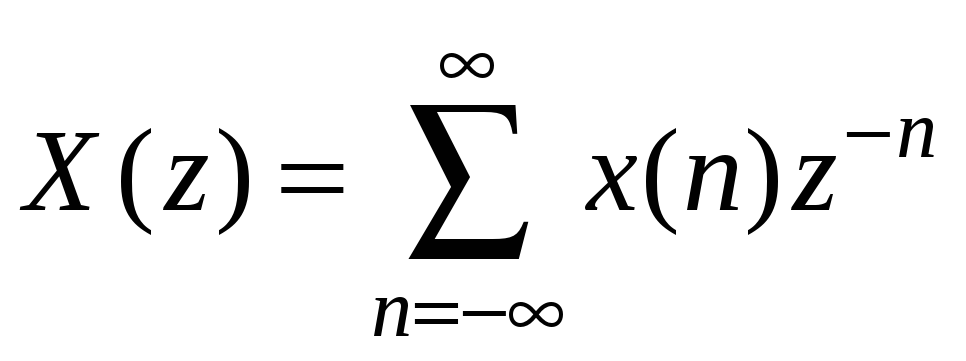
следует

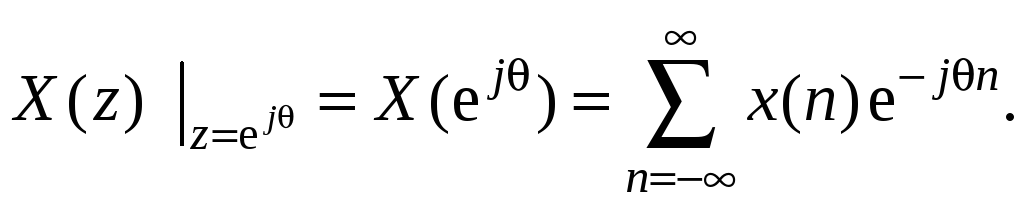(1.58)

Это выражение совпадает с выражением для преобразования Фурье исходной последовательности. Другими словами, преобразование Фурье является частным случаем z-преобразования, вычисленного на единичной окружности в z-плоскости.

Следует отметить, что единичная окружность в z-плоскости играет весьма важную роль. Например, имеются нереализуемые системы, такие как идеальный фильтр нижних частот или идеальный дифференциатор, z-преобразование которых сходится только на единичной окружности, т. е. эти системы имеют Фурье-преобразование, но не имеют z-преобра­зования.

Наконец, необходимо отметить, что если все особые точки расположены внутри круга единичного радиуса на z-плоскости, то система с соответствующей импульсной характеристикой будет устойчивой.