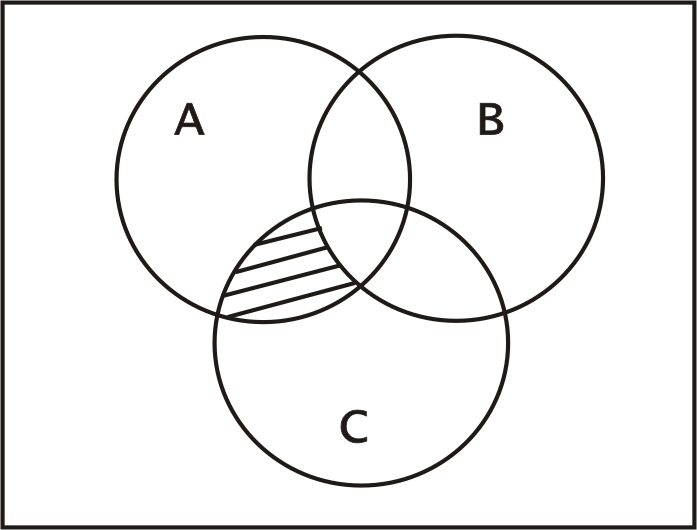
2.2.4. Кола Ейлера як інструмент графічного зображення в теорії множин

Розглянемо інструмент ілюстрації в теорії множин, кола Ейлера, для графічного зображення всіх операцій перерізу з трьома множинами (рис.2.9).

1)	2)	3)	4)
5)	6)	7)	8)

1)	2)	3)	4)
5)	6)	7)	8)

Рис.2.9.

Тут зображені всі варіанти розбиття площини універсуму , якщо в операціях задіяні три множини. Ці варіанти можна використовувати для графічного зображення будь яких операцій з трьома множинами. Їхній алгебраїчний вираз можна використовувати для алгебраїчного запису результату операції з множинами. Наведемо приклади.

Приклад 2.16. На колах Ейлера зображено результат операцій з множинами. Виходячи з зображення навести результат в алгебраїчному вигляді.

1.

Рис.2.10.

.

Ми використали поняття розбиття універсуму. Але для алгебраїчного вигляду можна знайти і інші варіанти. Наприклад,

і т.д.

2.

Рис.2.11.

3.

Рис.2.12.

Як ви вже мабуть побачили, що аналогічно формулам алгебри логіки формули алгебри множин теж мають кілька різних варіантів. Ці варіанти відрізняються операціями і кількістю множин, що входять у формулу. Причому вираз, в який входять об’єднання перерізів всіх множин не тільки не є самим коротким, а навпаки є найдовшим. Чи не нагадує він ДДНФ для логічної функції? Якщо ви згадаєте означення ДДНФ, то побачите повну аналогію. Для логічних функцій побудова ДДНФ була першим етапом алгоритмів скорочення формул. В теорії множин це питання не стоїть так гостро. Значно більше значення має проблема доведення тотожностей.

Вправа 2.2.

1. Довести рівність множин, використовуючи

а) означення рівності або твердження про рівність множин;

б) метод алгебраїчних перетворень:

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

2. Прийнявши множину перших 20 натуральних чисел як універсум , запишіть його підмножини:

– парних чисел;

– непарних чисел;

– квадратів чисел;

– простих чисел;

і запишіть множини, які одержують в результаті наступних операцій:

1)	7)
2)	8)
3)	9)
4)	10)
5)	11)
6)	12)

3. Множини представлені колами Ейлера. Записати за допомогою операцій над множинами вирази для множин, відповідно заштрихованим областям:

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)	12)

4. Доведіть тотожність, методом алгебраїчних перетворень.

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) ;

10) ;

11) ;

12) .

5. Надані множини, , , . Знайти декартів добуток множин:

1)	7)
2)	8)
3)	9)
4)	10)
5)	11)
6)	12)