
- •Розділ iі Множини
- •2.1. Основні поняття теорії множин
- •2.1.1. Способи подання множин
- •2.1.2. Порожня множина
- •2.1.3. Операції над множинами
- •2.1.4. Універсум
- •2.1.5. Підмножина. Рівність множин.
- •2.1.6. Множина підмножин
- •2.2 Алгебра множин
- •2.2.1. Закони алгебри множин
- •1. Комутативні закони
- •2. Асоціативні закони
- •3. Дистрибутивні закони
- •2.2.2 Методи доведення тотожностей алгебри множин
- •2.2.3. Узагальнення операцій над множинами, розбиття множини, декартів добуток множин.
- •2.2.4. Кола Ейлера як інструмент графічного зображення в теорії множин
- •2.3 Нечіткі множини та лінгвістичні змінні
- •2.3.1 Загальні відомості та означення
- •2.3.2. Теоретико-множинні операції з нечіткими множинами.
- •2.3.3. Включення і рівність нечітких множин
2.1.2. Порожня множина
У теорії множин використовується поняття порожньої множини. Позначається вона символом .
Множина може взагалі не містити елементів, наприклад
![]() – непарне
число, що ділиться на
– непарне
число, що ділиться на
![]() ;
;
![]() .
.
Для позначення цього факту вводиться поняття порожньої множини.
Це поняття відіграє дуже важливу роль при заданні множин за допомогою опису. Так, без поняття порожньої множини не можна говорити про множину відмінників групи 1ЕК спеціальності “Економічна кібернетика” або про множину дійсних коренів квадратного рівняння, не пересвідчившись заздалегідь, чи є взагалі в студентській групі відмінники або чи має задане рівняння дійсні корені. Поняття порожньої множини дає змогу оперувати множиною відмінників групи, не піклуючись про те, чи є відмінники в групі, яка розглядається. Теж саме стосується й множини дійсних коренів квадратного рівняння. Порожню множину умовно будемо відносити до скінченних множин. Можна довести, що порожня множина єдина.
Таким чином, уведення порожньої множини дає можливість оперувати будь-якою множиною без попереднього застереження, існує вона чи ні.
2.1.3. Операції над множинами
Розглянемо дві множини А та В і введемо кілька операцій над ними. Для графічної ілюстрації будемо використовувати кола Ейлера. Для зображення множини на площині креслять замкнену лінію із заштрихованою внутрішньою областю (найчастіше – це коло, звідси й назва відповідного інструмента, що широко застосовується в теорії множин).
Зазначимо,
що в подальшому викладі використовуватимемо
символи вже відомих нам логічних операцій
кон’юнкції «![]() »
диз’юнкції «
»
диз’юнкції «![]() »
імплікації «
»
імплікації «![]() »,
еквіваленції «
»,
еквіваленції «![]() »
для формалізованого запису означень і
теорем.
»
для формалізованого запису означень і
теорем.
Означення
2.1.
Об’єднання
![]() і
і
![]() (
(![]() )
– множина, що складається з усіх елементів
множини
)
– множина, що складається з усіх елементів
множини
![]() ,
всіх елементів множини
,
всіх елементів множини
![]() і не містить ніяких інших елементів
(рис.2.1), тобто
і не містить ніяких інших елементів
(рис.2.1), тобто
![]() ,
,
де символ
«![]() »
позначає логічну операцію диз’юнкції
(логічне «або»), тобто, згадуючи операцію
„диз’юнкція”, елемент
»
позначає логічну операцію диз’юнкції
(логічне «або»), тобто, згадуючи операцію
„диз’юнкція”, елемент
![]() належить множині
належить множині
![]() тоді і тільки тоді, коли або
тоді і тільки тоді, коли або
-
 істинне
і
істинне
і
 хибне, або
хибне, або -
 істинне
і
істинне
і
 хибне, або
хибне, або -
 істинне
і
істинне
і
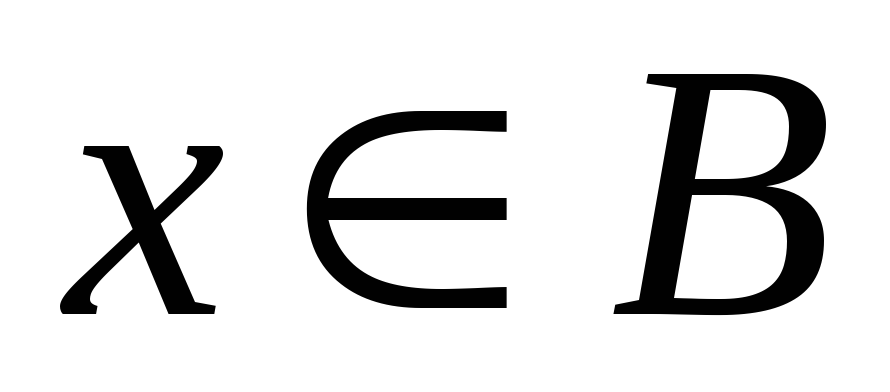 істинне.
істинне.

Рис.2.1
Означення
2.2.
Переріз
![]() і
і
![]() – множина, що складається з тих і тільки
тих елементів, які належать одночасно
множині
– множина, що складається з тих і тільки
тих елементів, які належать одночасно
множині
![]() та множині
та множині
![]() (рис.2.2), тобто
(рис.2.2), тобто
![]() ,
,
де символ
«![]() »
позначає логічну операцію кон’юнкції
(логічне «і»), тобто згадуючи операцію
„кон’юнкція”, елемент
»
позначає логічну операцію кон’юнкції
(логічне «і»), тобто згадуючи операцію
„кон’юнкція”, елемент
![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли
![]() і
і
![]() істинні одночасно.
істинні одночасно.

Рис.2.2
Означення
2.3.
Різниця
![]() і
і
![]() (відносне доповнення) – множина, що
складається з тих і тільки тих елементів,
які належать множині
(відносне доповнення) – множина, що
складається з тих і тільки тих елементів,
які належать множині
![]() й не належать
й не належать
![]() (рис.2.3), тобто
(рис.2.3), тобто
![]() .
.
Тобто,
елемент
![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли
![]() істинне і
істинне і
![]() хибне одночасно.
хибне одночасно.

Рис.2.3
Означення
2.4.
Диз’юнктивна
сума
![]() і
і
![]() (симетрична різниця) – множина, що
складається з усіх елементів
(симетрична різниця) – множина, що
складається з усіх елементів
![]() ,
які не належать множині
,
які не належать множині
![]() ,
й усіх елементів
,
й усіх елементів
![]() ,
які не належать множині
,
які не належать множині
![]() ,
та яка не містить ніяких інших елементів
(рис.2.4), тобто
,
та яка не містить ніяких інших елементів
(рис.2.4), тобто
![]() .
.
Тобто,
елемент
![]() тоді і тільки тоді, коли або
тоді і тільки тоді, коли або
-
 істинне
і
істинне
і
 хибне одночасно, або
хибне одночасно, або -
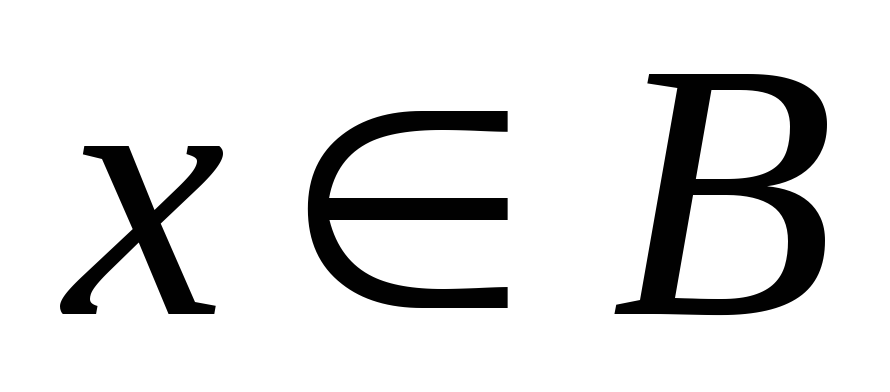 істинне
і
істинне
і
 хибне одночасно.
хибне одночасно.

Рис.2.4
Очевидно, що
![]() .
.
Вправа 2.1.
1. Задати всіма можливими способами множини:
-
непарних чисел, які є меншими за 20;
-
всіх непарних чисел;
-
цифр вісімкової системи зчислення;
-
чисел, кратних 5;
-
чисел, кратних 7;
-
парних чисел, які є більшими за 10;
-
парних чисел, які є меншими за 100;
-
чисел, кратних 3 і 5 одночасно;
-
чисел, кратних 4 і 7 одночасно;
-
квадратів натуральних чисел;
-
квадратів парних чисел;
-
квадратів непарних чисел.
