8.2 Форма модели косвенного контроля.
Сформируем следующую постановку задачи.
В пространстве ограниченного количества
измеряемых ИС параметров
необходимо построить модель
и для упрощения этой процедуры рассмотрим
два вспомогательных вопроса: выбор
структуры (формы) модели
и критерия достоверности модели
.
Каким бы ни был вид функции
,
её нужно сконструировать таким образом,
чтобы неизвестные коэффициенты этой
функции относительно min
критериев достоверности модели
определялись простым путем.
Чаще всего для этого используют суперпозицию типовых функций, например степенных:
Существует несколько возможных походов к решению поставленной задачи в зависимости от типа критерия достоверности:
- неизвестный вектор
определяется из решения вспомогательной
системы линейных уравнений.
- неизвестный вектор
определяется путем решения вспомогательной
задачи линейного программирования.
Использование критерия
и формы модели
по существу составляет основу хорошо
известного метода наименьших квадратов.
Задача построения модели осуществляется
в цикле: линейная модель
,
квадратичная, кубическая и т.д., пока не
достигнем заданной точности:
Продемонстрируем метод наименьших квадратов на простом примере. Пусть ищется модель типа полинома степени m.
Искомые коэффициенты полинома определяются из условия:
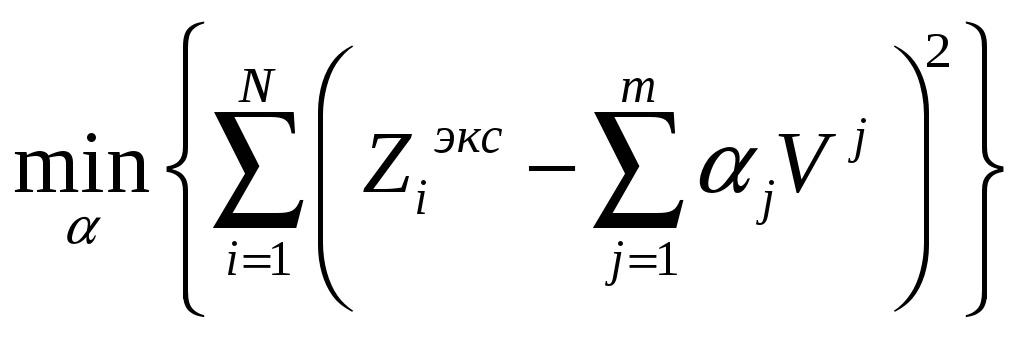
Дифференцируя по
и приравнивая значения всех производных
нулю, получим систему линейных уравнений
(переобозначим
)
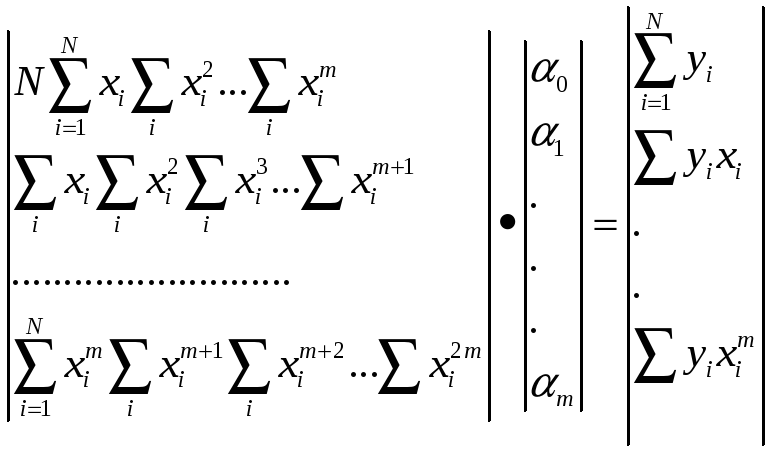
Для получения искомого вектора
необходимо произвести обращение матрицы
одним из стандартных способов.
Заметим, что при другой форме модели
задачу минимизации
и поиска вектора
приходится решать поисковым методом
численной оптимизации, что значительно
сложнее. Поэтому её обычно решают в
интерактивном режиме, когда пользователь
имеет возможность варьировать форму
модели, число параметров, типы критериев,
методы оптимизации и т.д.
Погрешность модели косвенного контроля имеет три составляющие:
Составляющая погрешности измерения
является взвешенной суммой погрешностей
отдельных измерений и вклада в модель
8.3. Компенсация и учёт динамики в системах косвенного контроля.
Главная причина динамической погрешности
заключается в том, что искомый показатель
и измеренный показатель находятся в
разных пространствах измерений.
Различают следующие методы компенсации динамической погрешности:
1) Учет запаздывания
- Введение запаздывания
, где
– взаимно-корреляционная функция:
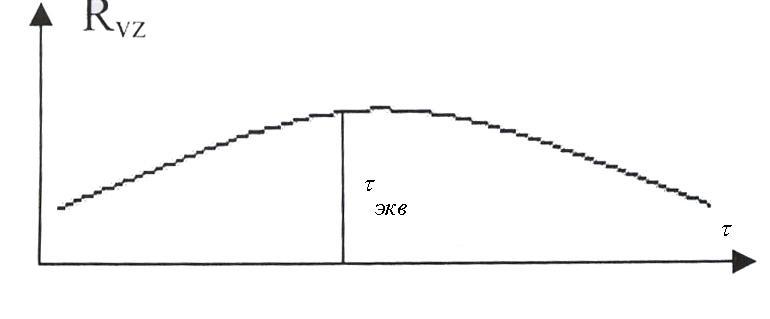
Для заданной дискретности измерений
имеем соответствие:
.Тогда, для каждого
используем значение
,
относительно которого строится модель.
- коррекция параметров запаздывания за
счет вычисления коэффициентов веса
линейной формы:
2) Эквивалентное интегрирование
- замена текущего значения
его средним значением (интегралом) на
интервале
,
чаще всего выбирается простейшая форма
– скользящее среднее
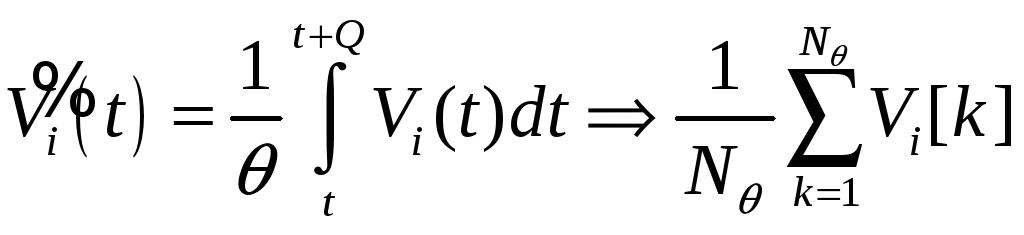
- коррекция параметров интегратора в линейной форме
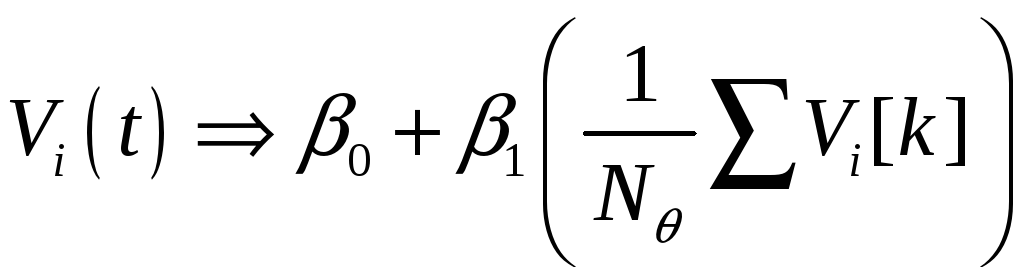
3) Одновременное введение запаздывания и скользящего среднего:
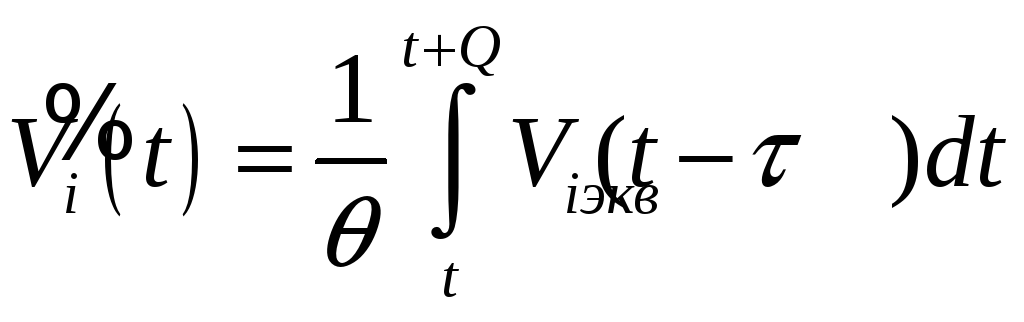
Как и ранее, результат компенсации динамики может быть улучшен в линейной форме трансформации измерений:
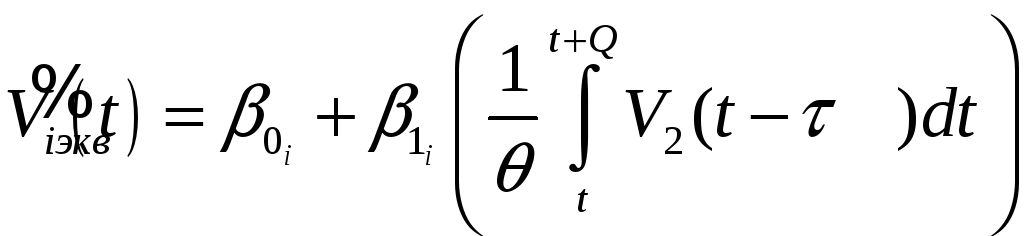
Заметим, что значения
и Q являются разными для
разных показателей
пространства измерений, так же как и
коэффициенты линейных форм
.
Процесс определения всех этих параметров
систем компенсации динамики стремятся
формализовать и упростить разными
вспомогательными приемами, но принципиально
они остаются неизменными: запаздывание,
усреднение, линейные формы [6].