Глава 8. Построение моделей косвенного контроля.

Будем, без потери общности, рассматривать следующую структуру, которая характерна для задач управления качеством (см. гл. 6).

Объект

УВМ

модель

Здесь нам через ИС доступны для измерения часть параметров на входе, выходе и в промежуточных точках, включая управление, т.е. пространство измерений . Необходимо построить модель, которая с позиций некоторого критерия идентификация была бы как можно ближе к недоступному для непосредственного контроля вектору состояний . В частности это могут некоторые показатели качества, количество которых [Z] обычно невелико – от 1 до 3 (5). Тогда искомая модель должна давать оценку истинного значения с некоторой погрешностью , или иначе , где – суммарная погрешность, которая обусловлена погрешностью измерений и погрешностью, связанной с динамическими свойствами объекта: .

8.1. Особенности построения модели косвенного контроля.

I этап: выбор измеряемого пространства.

Обычно на I этапе желательно, чтобы пространство измерений содержало max 40-50 измеряемых параметров.

II этап: профессиональный анализ.

Здесь количество параметров может быть частично уменьшено (до 25-30) либо изменено за счет каких-либо профессиональных знаний (технолога, специалиста по управлению, менеджеров среднего звена).

III этап: редукция пространства измерений.

Обычно используется два подхода: 1) нелинейные функциональные преобразования; 2) статистическая линеаризация пространства измерений. Рассмотрим эти подходы отдельно, хотя, конечно, их можно использовать одновременно.

3.1 Идея функциональных преобразований сводится к тому, что предварительно вычисляются некоторые соотношения измеряемых параметров для последующего использования в модели. Формально, модель в пространстве таких “обобщенных” измерений будет содержать меньше переменных. Примеры таких функциональных соотношений:

Иногда используются для этих целей т.н. инварианты, которые известны в данной предметной области, например для механических систем часто используется такой показатель, как Re – число Рейнольдса:

где – скорость, - линейный размер, - вязкость (кинематическая).

Подобные инварианты известны в разных предметных областях (теплотехнике, химической технологии, электромеханике): Nu,Pe,Prl,Da … и их использование было особенно характерно для “докомпьютерной” эры моделирования. В последнее время поиском таких соотношений стали вновь активно заниматься (синергетический подход).

8.2 Статистический анализ объекта

Статистический анализ обычно проводят в одной из форм: - активный эксперимент для выявления параметров с наибольшим влиянием на искомый показатель в области его экстремального значения; - пассивный эксперимент, для которого характерно длительное наблюдение за системой (объектом) без вмешательства в нормальный ход его функционирования.

На время статистического эксперимента необходимо организовать достаточно частое измерение показателей качества. (Чаще чем обычно в 4-5 раз). Полученные данные обрабатываются статистическими методами и получаются математические ожидания, дисперсии и другие статистические характеристики.

[N]=200-300 наблюдений.

Интервал наблюдений обычно находится из корреляционных функций выходных координат.

Пусть – это то, что определяет пространство измерений в k-тый момент времени. С использованием измеренных во время эксперимента показателей качества с той же частотой измерения, вычисляем для всего множества наблюдений k=1,N статистические характеристики. Если измеряется один показатель , то тогда:

1) Коэффициенты взаимной корреляции для Z и составляют вектор:

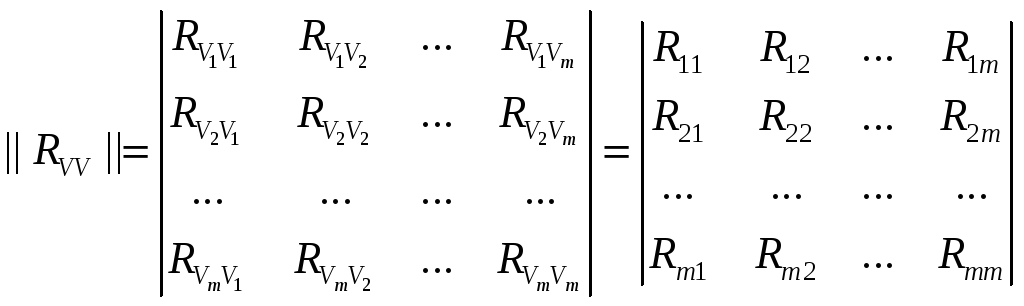
2) Коэффициенты корреляции всех измерений между собой составляют матрицу :

Редукция сводится к работе двух фильтров:

1 фильтр (убирает параметры , слабо влияющие на искомый z) работает по следующему принципу:

- если , то отбрасывается измеряемый параметр . Обычно выбирают

2 фильтр (убирает дублирующие, сильно связанные между собой параметры) путем сравнения с порогом :

- если , то отбрасывается тот из этой пары, который слабее влияет на z, т.е. тот для которого выполняется условие . Обычно = 0,8 - 0,9.

Эту процедуру повторяют несколько раз, варьируя значениями порогов обоих фильтров ( и ) до получения искомого результата: сокращения размерности [v] до 10-15. Далее переходим к следующему этапу - построению модели.