7.4. Дискретные объекты и передаточные функции.
Обычно используется для этих целей
аппарат z-преобразования,
в соответствии с которым любой функции
ставится в соответствие некоторая
дискретная (решётчатая) функция
,
где
–
период дискретности (квантования по
времени). По аналогии с преобразованием
Лапласа вводится преобразование:
с помощью которого можно получить дискретную передаточную функцию:
Для большинства физических объектов
.
В известных пособиях по импульсным
системам [6,7] приводятся в качестве
справки таблицы перехода от непрерывных
передаточных функций к дискретным,
например для типовых звеньев:
|
№ |
W(s) |
G(z) |
Расчет коэффициента |
Примечание |
|
1 |
|
|
|
Инерционный объект 1-ого порядка |
|
2 |
|
|
|
Звено запаздывания |
|
3 |
|
|
|
Последовательное соединение двух звеньев |
|
4 |
|
|
|
Объект с неминимально-фазовой характеристикой |
|
5 |
|
|
|
Фильтр низких частот запаздывания |
Эти типовые объекты (1-5) используются
для определения оптимальных настроек
в алгоритмах регулирования. Обратим
внимание, что при переходе к
коэффициенты
пересчитываются с учетом интервала
дискретности
,
как это показано для объектов (1,2).
Соответственно и получаемые оптимальные
настройки
зависят тоже от
.
Примеры подобных зависимостей см. в
[5].
7.5. Моделирование дискретных систем
Пусть задан многомерный линейный объект в виде:
|
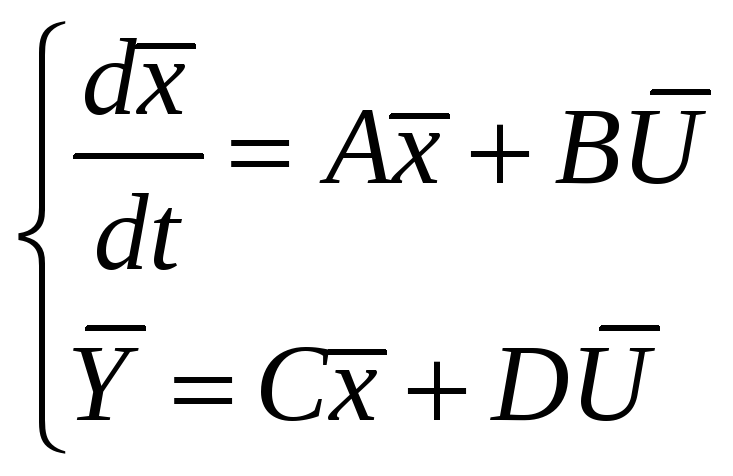системы дифференциальных равнений в
форме Коши.
где А,В матрицы параметров пространства (состояний) Х(t)
- вектор управлений;
- пространство измерений.
C,D – матрицы
параметров пространства измерений.
(Заметим, что
и
переставимы по смыслу задачи).
Аналогом такого объекта является система:
и схема её моделирования.
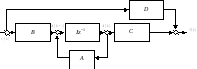
Рис. 7.5
Объекты с запаздыванием z-d
представляются цепочкой с несколькими
единичными
запаздываниями (здесь d=3).
В общем случае различают объекты с запаздыванием по управлению, с запаздыванием по измерению и др.
Соответствующие уравнения имеют вид:
(задержка
на выходе)
(задержка
по управлению)
В последнем случае структура схемы
моделирования аналогична рис. 7.3, но
появляется запаздывание в канале
управления (обратим внимание на несколько
иное выражение для
).
Задержка по управлению имитирует
скорость обработки информации.
Несколько более сложно вводится внутренняя задержка [5]. Ещё раз подчеркнем, что понятие пространства состояний и измерений переставимы по физическому смыслу.
Обычно используется квадратичный критерий качества, например, типа:
,
в котором учтены конечное состояние Х[N], текущие состояния Х[k] и затраты на управление с определёнными требованиями к матрицам S,Q,R, включая условия существования min I, условия устойчивости и др.
Подобные структуры дискретных объектов используются в системах управления с “наблюдателем”, однако из-за того, что этот класс моделей – линейный, требуется постоянная коррекция коэффициентов таких моделей – т.н. идентификация.
Это обстоятельство следует учесть, т.к. мы фактически переходим к адаптивным системам (см. §6.5) или их модификациям.
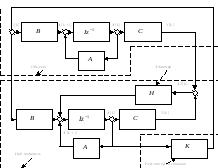
Ранее было указано на невозможность использования ПИД-законов управления для объектов с большим запаздыванием, системы с “наблюдателем” позволяют преодолеть это ограничение. Пример соответствующей структуры приведен в ряде работ, т.н. учредитель Смита [ 5 ].