
- •Глава 7. Особенности цифровой реализации систем динамической стабилизации
- •7.1. Цифровая реализация пид-законов регулирования.
- •7.2. Форсированное управление.
- •7.3. Центральный регулятор.
- •7.4. Дискретные объекты и передаточные функции.
- •7.5. Моделирование дискретных систем
- •Глава 8. Построение моделей косвенного контроля.
- •8.1. Особенности построения модели косвенного контроля.
- •8.2 Статистический анализ объекта
- •8.2 Форма модели косвенного контроля.
- •8.3. Компенсация и учёт динамики в системах косвенного контроля.
- •8.4. Свойства линейности и адаптации.
Глава 7. Особенности цифровой реализации систем динамической стабилизации
Структура закона управления
![]() чаще
всего задается некоторыми типовыми
соотношениями, содержащими вектор
параметров настройки (по данным
предварительного моделирования), который
в последующем адаптивно корректируется
в режиме реального времени –
чаще
всего задается некоторыми типовыми
соотношениями, содержащими вектор
параметров настройки (по данным
предварительного моделирования), который
в последующем адаптивно корректируется
в режиме реального времени –
![]() на рис 6.2,
на рис 6.2,
![]() на рис 6.6.
на рис 6.6.
Простейший вид
![]() – это т.н. ПИД-регулятор, или точнее
ПИД-закон регулирования (алгоритм).
– это т.н. ПИД-регулятор, или точнее
ПИД-закон регулирования (алгоритм).
Математическая реализация алгоритма ПИД-регулятора выглядит следующим образом:
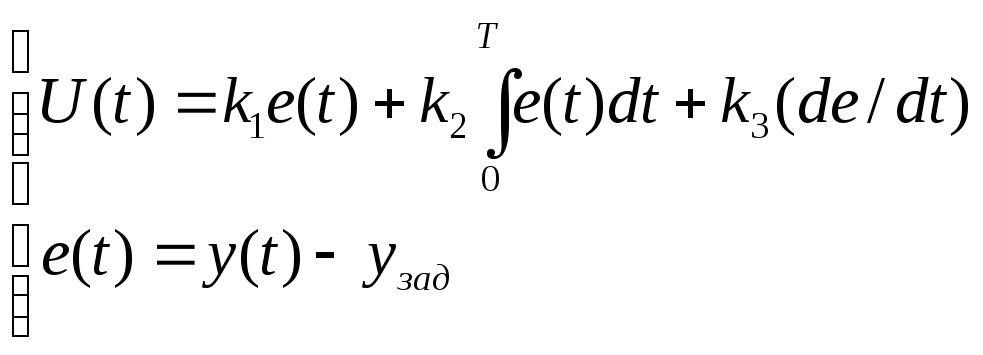 //
Он записан здесь для одномерного
(скалярного) случая
//
Он записан здесь для одномерного
(скалярного) случая
7.1. Цифровая реализация пид-законов регулирования.
Для алгоритма цифровой реализации важно
выбрать некоторый интервал дискретности
управления
![]() и измерения
и измерения
![]() .
Будем для простоты предполагать, что
они совпадают и нас будут интересовать
вычисления в дискретном времени [k].
.
Будем для простоты предполагать, что
они совпадают и нас будут интересовать
вычисления в дискретном времени [k].
![]() и тогда существует переход
и тогда существует переход
![]() и т.д. Соответственно все составляющие
и т.д. Соответственно все составляющие
![]() должны иметь свой дискретный аналог;
тогда ПИД закон регулирования
трансформируется:
должны иметь свой дискретный аналог;
тогда ПИД закон регулирования
трансформируется:
![]()
и с использованием численных методов интегрирования и дифференцированно (их может быть несколько вариантов-альтернатив) получим разные дискретные аналоги.
Например,
![]()
Здесь правая часть представляет собой конечно-разностную реализацию интегральной части по алгоритму интегрирования методом прямоугольников. В содержательной постановке (следуя [5]) закон ПИД-регулирования имеет вид в цифровой форме (для одной переменной):
![]() (2)
(2)
![]() - обобщенный коэффициент передачи
центрального регулятора;
- обобщенный коэффициент передачи
центрального регулятора;
![]() - такт квантования;
- такт квантования;
![]() - время интегрирования;
- время интегрирования;
![]() - время дифференцирования (постоянная
времени дифференцирования).
- время дифференцирования (постоянная
времени дифференцирования).
7.2. Форсированное управление.
Стремясь упростить выражение для
![]() ,
поступим следующим образом: запишем
управление для
,
поступим следующим образом: запишем
управление для
![]() и найдем значение для приращения
управления
и найдем значение для приращения
управления
![]() ;
тогда получим:
;
тогда получим:
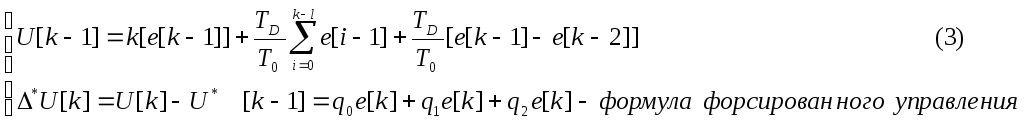 которая
показывает, что
которая
показывает, что
![]() (приращение управления) – это линейная
комбинация ошибок
(приращение управления) – это линейная
комбинация ошибок
![]() на нескольких предыдущих шагах управления;
в более общем виде:
на нескольких предыдущих шагах управления;
в более общем виде:
![]() (4)
(4)
где l – количество шагов “назад” зависит от принятых численных методов.
Замечание – нужно иметь в виду, что
теоретическое и истинное значение
управления могут отличаться, поэтому
при форсированном управлении значение
![]() должно строго контролироваться. Значения
коэффициентов
должно строго контролироваться. Значения
коэффициентов
![]() зависят от метода интегрирования.
зависят от метода интегрирования.
Так для метода прямоугольников: для метода трапеций:
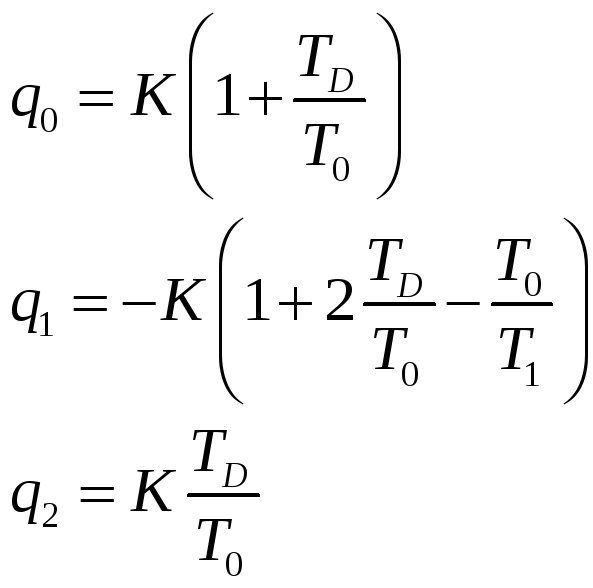
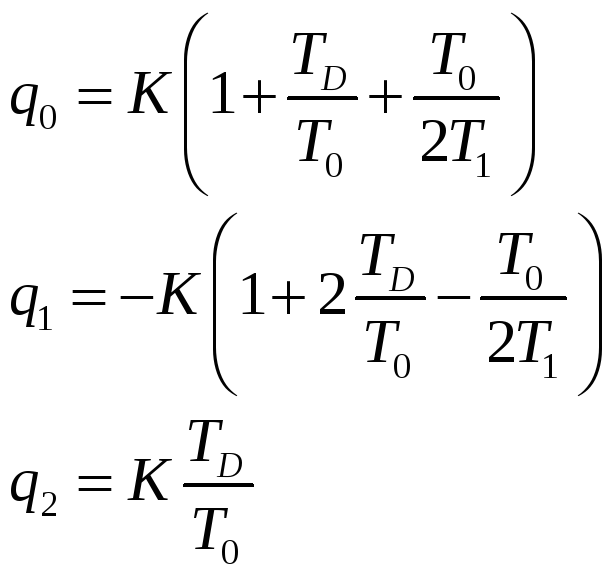
Аналогично может быть проанализировано
влияние методов дифференцирования на
окончательный вид
![]() .
.
7.3. Центральный регулятор.
Главная идея центрального регулятора
заключается в следующем: при цифровом
управлении многоконтурным объектом (в
окрестности малых ошибок, когда верна
гипотеза линейности) делается
предположение, что все контуры работают
независимо и управление осуществляется
по одному закону, (например, ПИД), но с
разными коэффициентами
![]()
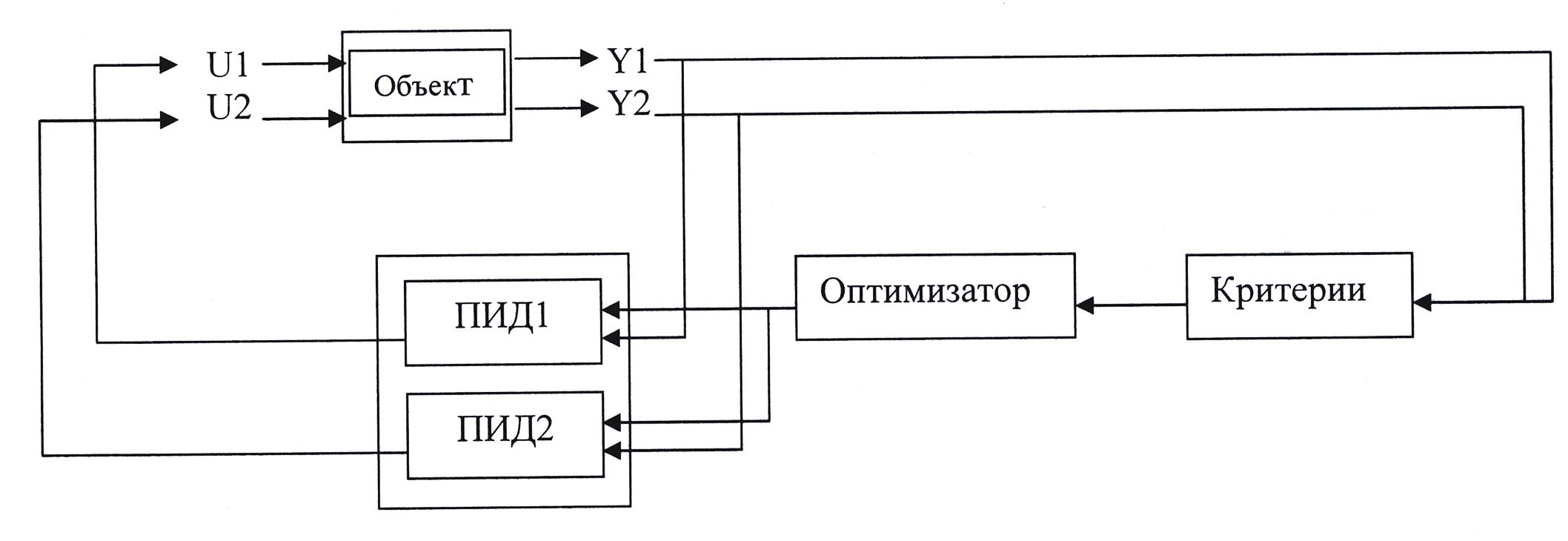
Рис. 7.1
Структурная схема центрального регулятора представлена выше (рис. 8.4) для простейшего объекта с двумя контурами регулирования.
Чтобы установить настройку для ij–ого контура необходимо знать динамические свойства объекта. Определение динамических свойств линейных объектов происходит путем подачи на вход тестового воздействия.
В связи с этим выделяют различные типы воздействий по управлению.
Тестовые воздействия по управлению могут быть разных типов:
a) импульсное воздействие:
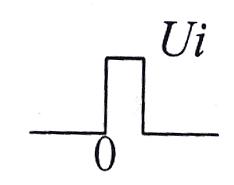 a)
a)
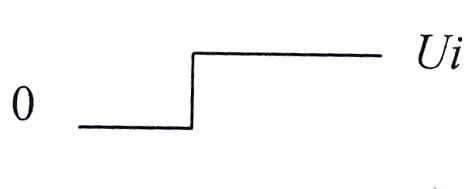
b) скачкообразное (ступенчатое) b)
c) частотное: c)
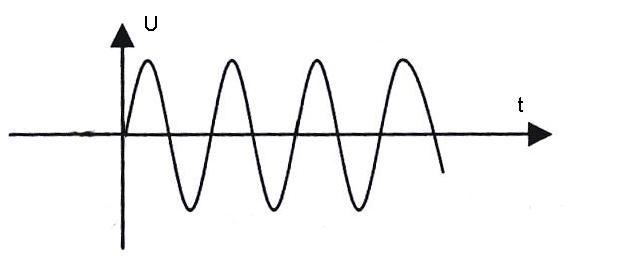
Рис. 7.2 (a,b,c,d)
Обычно, это синусоида, с попеременным
изменением частоты в диапазоне от
![]() до
до
![]() .
.
d) произвольное воздействие(прямоугольная волна):
d)
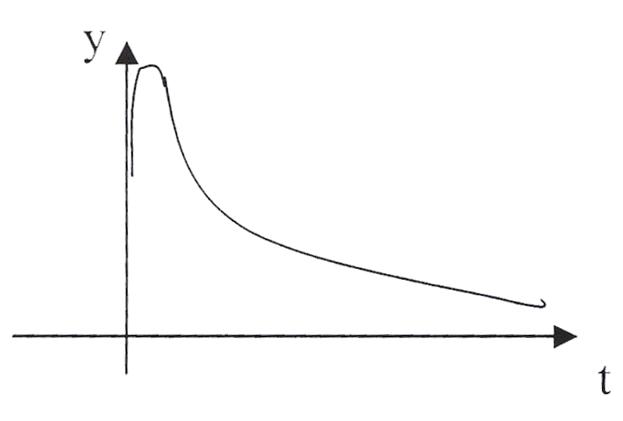
Соответственно каждому типу входного воздействия будет соответствовать свой тип реакции на выходе объекта.
a) Реакция на импульсное воздействие:
b) Реакция на ступенчатое воздействие (скачок):
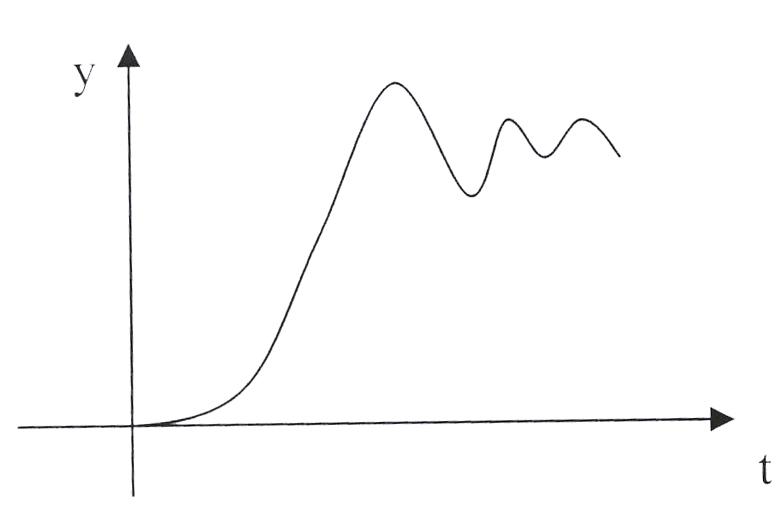
Рис. 7.3 (a,b)
d) Реакция на частотное воздействие после обработки сводится к построению частотных характеристик (АЧХ, ФЧХ, АФЧХ), пример амплитудно-фазовой характеристики на рис. 6.4
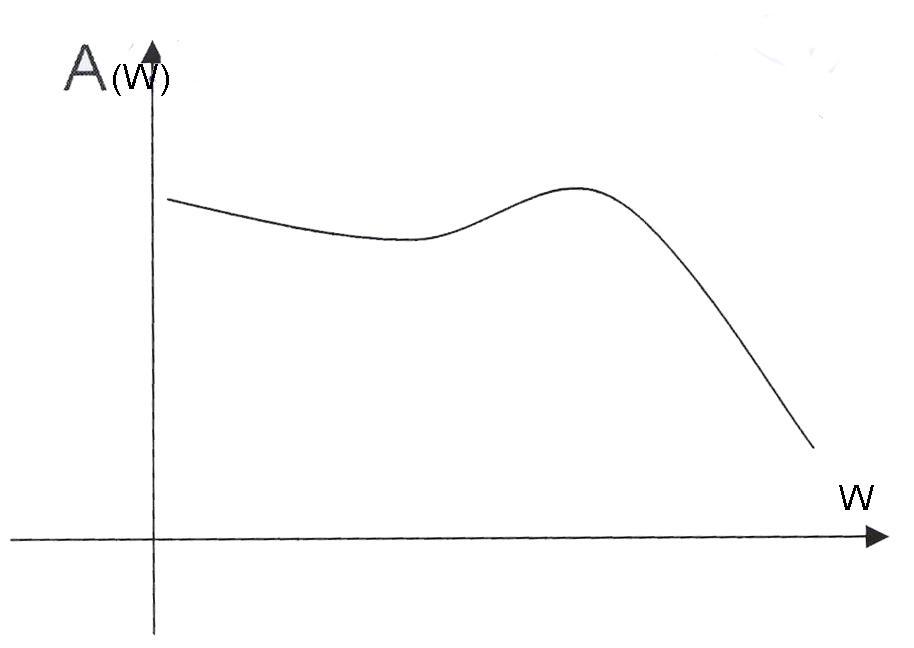
Рис. 7.4
Цель такого исследования - получить
передаточную функцию
![]() .
.
Для ПИД регулирования достаточно объект
представить по каждому каналу “![]() ”:
”:
![]() ,
где
,
где
![]() - коэффициент усиления
- коэффициент усиления
![]() – постоянная времени 1 и 2 - го порядка
– постоянная времени 1 и 2 - го порядка
![]() - время запаздывания
- время запаздывания
 - коэффициент усиления.
- коэффициент усиления.
Для построения контура динамической
стабилизации необходимо знать:
![]() .
.
В зависимости от значений этих коэффициентов определяется целесообразность использования режим ПИД-регулятора:
A) Если
![]() - можно пренебречь запаздыванием и
использовать простой закон усиления
по управлению К.
- можно пренебречь запаздыванием и
использовать простой закон усиления
по управлению К.
B) -
![]() - ПИД-регулятор применять нельзя,
необходимы дополнительные вычислительные
операции в управлении.
- ПИД-регулятор применять нельзя,
необходимы дополнительные вычислительные
операции в управлении.
C) -
![]() - ПИД управление целесообразно.
- ПИД управление целесообразно.
Тогда для каждого
![]() –ого
контура, где
–ого
контура, где
![]() - номер выходной координаты
- номер выходной координаты
![]() ,
,
![]() - номер координаты входного управления,
необходимо запомнить матрицу настроек
- номер координаты входного управления,
необходимо запомнить матрицу настроек
![]() размерностью 3xn и в
зависимости от комбинации
размерностью 3xn и в
зависимости от комбинации
![]() реализовать
один и тот же тип ПИД-регулятора (один
и тот же алгоритм), но со своими,
определенными путем моделирования,
настройками
реализовать
один и тот же тип ПИД-регулятора (один
и тот же алгоритм), но со своими,
определенными путем моделирования,
настройками
![]() .
Поскольку ИУВС постоянно контролирует
номер контура (не только в процессе
управления, но и в процессе измерения)
выбор необходимого вектора настроек
из базы настроек
.
Поскольку ИУВС постоянно контролирует
номер контура (не только в процессе
управления, но и в процессе измерения)
выбор необходимого вектора настроек
из базы настроек
![]() не представляет труда.
не представляет труда.
Замечание: при моделировании подобных
систем мы предполагаем, что объект
является непрерывным со своей передаточной
функцией
![]() либо матрицей передаточных функций для
объекта в целом
либо матрицей передаточных функций для
объекта в целом
![]() .
.
Если требования непрерывности объекта не соблюдаются, мы должны рассматривать его как дискретный и при моделировании внести соответствующие коррективы, которые основаны на понятиях дискретных или импульсных систем. Такой учёт дискретности нужен для “быстрых” объектов, переходные процессы в которых соизмеримы со временем обработки и прохождения информационных потоков в ЭВМ и других технических средствах (ЦАП, АЦП, каналы связи со средствами защиты) информационно-управляющей системы в целом. Наконец, в более сложных случаях объект можно представить как последовательное соединение дискретной и непрерывной (низкочастотной) частей.
