21. Расчетные формулы показателей восстановления.

Среднее время восстановления Тв – это математическое ожидание времени восстановления работоспособного состояния объекта после отказа.

Вероятность восстановления v (t) — это вероятность того, что время восстановления Тв объекта (элемента или системы) будет меньше времени t, т.е. не превысит заданного: v (t) = v (Tв < t).

Вероятность невосстановления w (t) — это вероятность того, что время восстановления Тв объекта (элемента или системы) будет больше или равно времени t: w (t) = w (Tв ≥ t) = 1 — v (t).

Интенсивность восстановления μ(t) в момент времени t, отсчитываемый от начала восстановления, — это отношение плотности вероятности восстановления к вероятности невосстановления:

μ(t) = v'(t)/w (t) = w'(t)/w (t). 

А время восстановления, например, выключателей можно определить по другой формуле. К примеру, при внезапных отказах выключателей отключившиеся элементы (генерирующие агрегаты, трансформаторы, ЛЭП) в большинстве случаев могут быть введены в работу раньше, чем будет произведен ремонт выключателя. При этом длительность их простоя (время восстановления) определяется временем, необходимым для выполнения переключений в РУ: Tср = T0 + Tрnр,                           

где T0 — постоянная составляющая, равная времени, необходимому для того, чтобы обслуживающий персонал мог прийти в РУ и установить характер повреждения (для подстанций с обслуживанием Т0 = 0,1 -0,3 ч);

Тр = 0,1 ч — время для отключения (включения) разъединителя;

nр — число разъединителей, которые должны быть отключены (включены) для отделения поврежденного выключателя и ввода отключившихся элементов в работу.

22. Метод дифференциальных уравнений Колмогорова.

В расчетах надежности объектов с большой интен-стью отказов (соответственно с малым средним временем наработки на отказ tн) исп-ся методы матем. теории массового обслуживания. Объекты систем электросн-ния хар-ся малой интен-стью отказа, большим tн на отказ, поэтому рассм-м один метод – метод диф. ур-ний Колмогорова. ДУ сост-ся по диаграмме состояний объекта в соотв-вии с правилом: кол-во ур-ний равно кол-ву состояний объекта на диаграмме. В левой части каждого ур-ния стоит производная вер-сти состояния объекта. Правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния – каждый член с «-», если в состояние – «+». Каждый член равен произведению интен-сти перехода, соответ-го данной стрелке, умнож-го на вер-сть того состояния, из кот. исходит стрелка (см. рис.).

(*)

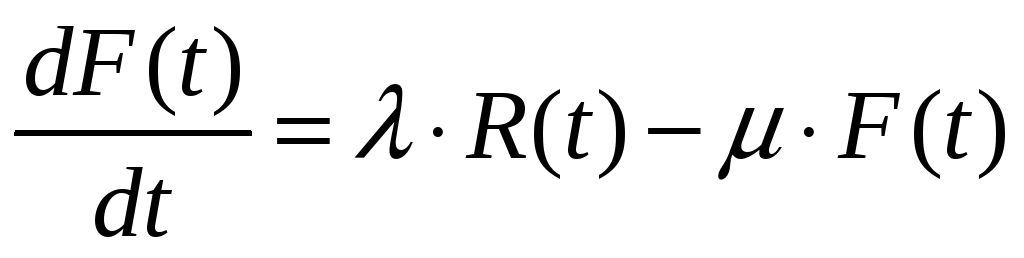
Т. к. F(t) и R(t) связаны (F(t)+R(t)=1), то можно огран-ся решением одного из ур-ний Колмогорова. Решая 1-ое ур-ние (*) при t=0, R(t)=1, F(t)=0 получим:

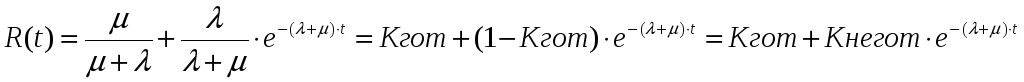
Kнегот численно равен вер-сти застать объект в неработоспособном состоянии в произвольное время. Кгот и К негот обр-ют полную группу несовместных событий, их сумма равен 1. Средние величины вер-стей безотк-ной работы и отказа в течение некот. фиксир. промежутка времени периода норм-ной эксплуатации могут быть вычислены:

;