
- •1.Электрическая система. Элементы, структура, режимы работы. Показатели, определяющие режимы работы системы.
- •2. Основные понятия теории вероятности.
- •10. Законы распределения случайных величин.
- •11. Определение вероятности, подчиняющейся нормальному закону распределения.
- •13. Определение вероятности по закону Пуассона.
- •14.Определение вероятности, подчиняющейся биноминальному закону распределения.
- •15. Качественные определения основных показателей надежности.
- •17. Аналитическая взаимосвязь основных показателей надежности.
- •18. Расчетные формулы показателей надежности, их упрощение и область применения.
- •19. Полная и расчетная диаграммы состояния объекта расчета надежности.
- •20.Количественные показатели восстановления.
- •21. Расчетные формулы показателей восстановления.
- •22. Метод дифференциальных уравнений Колмогорова.
- •23. Логические схемы расчета надежности.
- •24.Типовые логические схемы расчета надежности.
- •25. Частные случаи типовых логических схем расчета надежности
- •26.Правило Рябинина.
- •27.Реальные соединения элементов при расчете надежности.
- •28.Системы случайных величин и их характеристики. Функция распределения и плотность распределения системы случайных величин.
- •29.Числовые характеристики системы 2-х случайных величин.
- •30.Общие сведения о случайных функциях и процессах.
- •32. Стационарные и нестационарные случайные функции.
- •37. Критерий согласия (Пирсона, Колмогорова, ĩ).
- •38.Регрессионный анализ результатов измерения.
- •Цели регрессионного анализа
- •Математическое определение регрессии
- •40.Нелинейная регрессия.
- •41.Задачи электроснабжения, требующие поиска оптимальных решений.
- •43.Модели, применяемые для решения оптимизационных задач.
- •44. Классификация методов оптимизации.
- •45. Методы линейного планирования.
- •48. Каноническая форма задачи линейного планирования.
- •51.Симплекс-таблица задачи линейного планирования.
- •55.Градиентный метод решения задачи нелинейного планирования.
- •Алгоритм
- •56.Метод динамического планирования. Область применения и содержание.
- •57.Рекурентное соотношение методов динамического планирования.
- •58.Принцип оптимальности Белмана на примере задачи.
10. Законы распределения случайных величин.
Закон распределения случ-й в-ны – любое соотношение, устанавливающее связь между возможными значениями случ величин и соответствующими им вероятностями.
Для дискретной случ-й в-ны з-н распределения может быть представлен в виде таблицы, которая наз-ся рядом распределения. В котором перечисленные зн-я случ-й в-ны и соотв-е ей значение вер-ти. Графически получится многоугольник распределения вер-тей.
Для непрерывной случ-й в-ны представление закона распределения в табличной форме невозможно, т.к. число значений даже на ограниченном интервале ∞, поэтому для них определяют вер-ть попадания в интервал, а не в точку. Интервалы или ур-я возможность перейти для непрер-х случ-х в-н в табличной форме записи закон распределения
|
x |
x1 |
x2 |
… |
xn |
|
p |
p1 |
p2 |
… |
pn |
![]()
Для равномерного закона распределения неизменная плотность распределения вер-тей, ф-я распределения изменяется по линейному закону.
![]()
![]()
![]()
След-но φ(х)(b-a)=1, отсюда φ(x)=1/(b-a)
![]()
Функция распределения в точке а будет равна F(x)=(x-a)/(b-a) чем больше интервал тем меньше плотность.
Вер-ть попадания случ-й в-ны в интервал (c d) если он лежит внутри (a b) тогда F(c)<x<d= (d-c)/(b-a).
11. Определение вероятности, подчиняющейся нормальному закону распределения.
Плотность
распределения:
a- величина , характеризующая мат ожидание;
σ- величина, характеризующая стандартное отклонение. a, σ = const.

Вероятность:
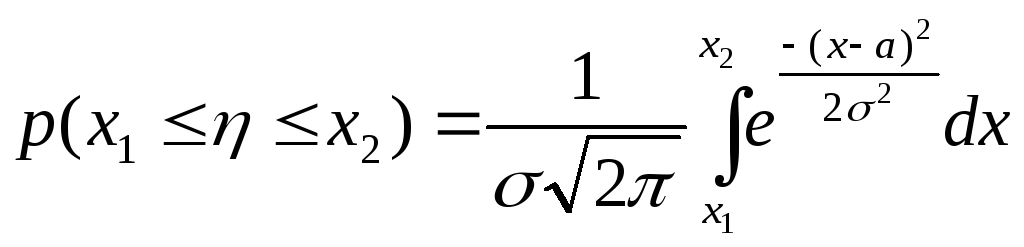
Нормальный закон распределения вероятностей описывается плотностью распределения. Для проведения расчётов, в которых используется нормальный закон, составляют таблицы

P(x1<x<x2) = (Ф(x2)-Ф(x1))/2
12. Определение вероятности, подчиняющийся равномерному закону распределения.
Величина, имеющая неизменную плотность вер-ти, наз-ся равномерным распределением случайной величины(СВ). При этом функция распределения изменяется по линейному закону. Если непрерывная случайная величина равномерно распределена в интервале (AB), то вер-ть попадания в этот интервал равна 1
![]()
Так как φ(х)=сonst, то след-но
![]()
Отсюда φ(х)=1/(b-a),
![]()
Чем больше интервал, тем меньше плотность распределения вер-тей. Вер-ть попадания случ-й в-ны в (СD) при условии (СD) лежит в (AB).
![]()
13. Определение вероятности по закону Пуассона.
Вероятность того что дискретная случайная в-на распределенная по Пуассону примет значение m, определяется
Pm =λm e-λ/m! .
Вер-ти значений распределенных по Пуассону составляет ряд
Р(0)=е-λ; Р(1)= λe-λ ;
P(2)=0.5λ2 e-λ ….
λ - постоянная величина. При малых значениях p и q вероятности различных значений случайных в-н по биноминальному закону близки к аналитическим вероятностям по Пуассону. Во многих случаях при малых p и q биноминальное распределение заменяют распределением по Пуассону.
