
- •II.Элементы функционального и комплексного анализа.
- •6. Формула включений и исключений.
- •Упражнения и задачи по теории множеств
- •III. Введение в математический анализ. Дифференциальное исчисление функции.
- •Вопросы для самопроверки:
- •Тема 2. Пределы
- •Вопросы для самопроверки:
- •Тема 3. Дифференциальное исчисление
- •Вопросы для самопроверки:
- •Тема 4. Приложения дифференциального исчисления
- •Вопросы для самопроверки:
- •Тема 5. Функции нескольких переменных
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •IV. Интегральное исчисление функции одной переменной.
- •Тема 1. Неопределенный интеграл
- •Вопросы для самопроверки.
- •Тема 6. Определенный интеграл
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •V. Дифференциальные уравнения.
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •VI. Числовые и функциональные ряды. Числовые ряды
- •Функциональные ряды
- •VII. Элементы теории вероятностей. Случайные события
- •Вопросы для самопроверки:
- •Сложные события Вопросы для самопроверки:
- •Повторение испытаний Вопросы для самопроверки:
- •Тема 12. Случайные величины Вопросы для самопроверки:
IV. Интегральное исчисление функции одной переменной.
Тема 1. Неопределенный интеграл
[1, гл IX, § 9.1 – 9.3],[4, гл VII]
Эффективным способом интегрирования функций является замена переменной. Его целью является получение с помощью новой переменной более простого интеграла.
Задача
1.
Найти
![]()
Решение:
Сделаем замену 2x=t. Для нахождения dx через t продифференцируем обе части уравнения:
![]() .
Теперь
.
Теперь
![]()
![]() .
.
Задача
2.
Найти
![]() .
.
Решение: 1-й способ. Сделаем замену
э![]()
Очевидно,
выразить dx
только через t
рациональным способом не удается.
Однако после подстановки полученных
выражений для
![]() и
dx
через t
исходный интеграл принимает вид:
и
dx
через t
исходный интеграл принимает вид:
![]() .
Можно было поступить по-другому. Нетрудно
видеть, что в равенстве
.
Можно было поступить по-другому. Нетрудно
видеть, что в равенстве
![]() левая часть содержит часть подынтегрального
выражения, а именно
левая часть содержит часть подынтегрального
выражения, а именно
![]() .
Поэтому
.
Поэтому
![]() и т.д.
и т.д.
2-й способ. Сделаем другую замену:
![]()
![]() и
подынтегральное выражение сразу очень
просто выражается через t:
и
подынтегральное выражение сразу очень
просто выражается через t:
![]() .
.
Вопросы для самопроверки.
1. Дайте определение первообразной.
2. Что называется неопределенным интегралом? Чем он отличается от первообразной?
3. Каковы основные методы интегрирования?
Тема 6. Определенный интеграл
[3, гл IX, § 9.4-9.6, зад и упр. 6-8,15,16],[4, гл IX, § 1-4].
Одним
из наиболее распространенных приложений
определенного интеграла является
решение физически задач. Если точка
движется по некоторой кривой со скоростью
V(t)≥0,
то путь пройденный точкой за время
![]() равен:
равен:
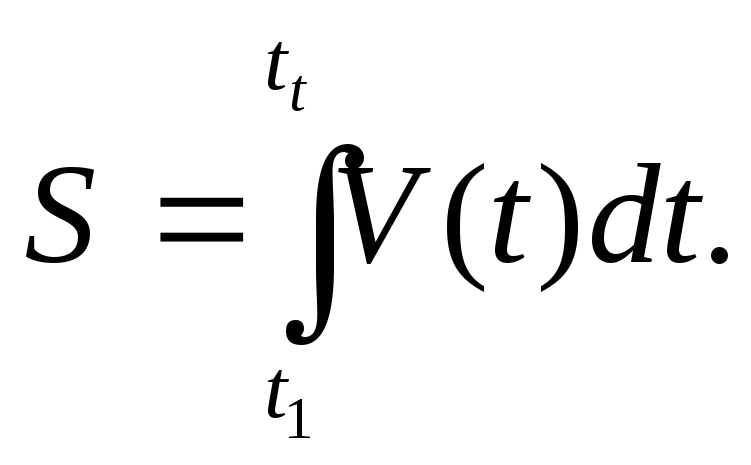
Задача
1.
Скорость точки равна
![]() (м/c).
Найти путь, который точка преодолела
за время t=4c,
прошедшее с начала движения.
(м/c).
Найти путь, который точка преодолела
за время t=4c,
прошедшее с начала движения.
Решение:
В нашем случае
![]()
![]() .
.
Вопросы для самопроверки:
-
Что называется определенным интегралом функции f(x) на отрезке [a;b]?
-
Каковы основные свойства определенного интеграла?
-
Каков геометрический смысл определенного интеграла?
-
Каковы особенности нахождения определенного интеграла с помощью подстановки?
-
Какие приложения определенного интеграла Вы знаете?
Задачи для самоконтроля
Найти неопределенные интегралы:
1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
2.
а)
![]() ;
б) а)
;
б) а)
![]() ;
в)
;
в)
![]() .
.
3.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
4.
а)
![]() б)
б)
![]() ;
в)
;
в)
![]() .
.
5.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
6.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
7.
а)
![]() ;
б)
;
б)
![]() 4
в)
4
в)
![]() .
.
8.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
9.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
10.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)
![]() .
.
Вычислить определенные интегралы:
11.
![]() 16.
16.
![]()
12.
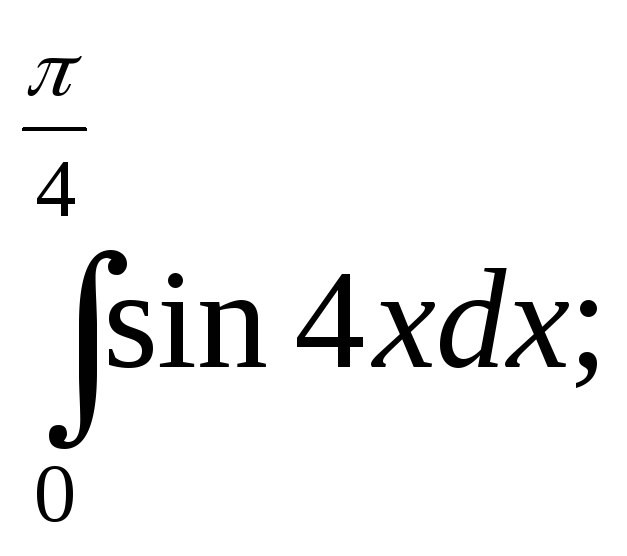 17.
17.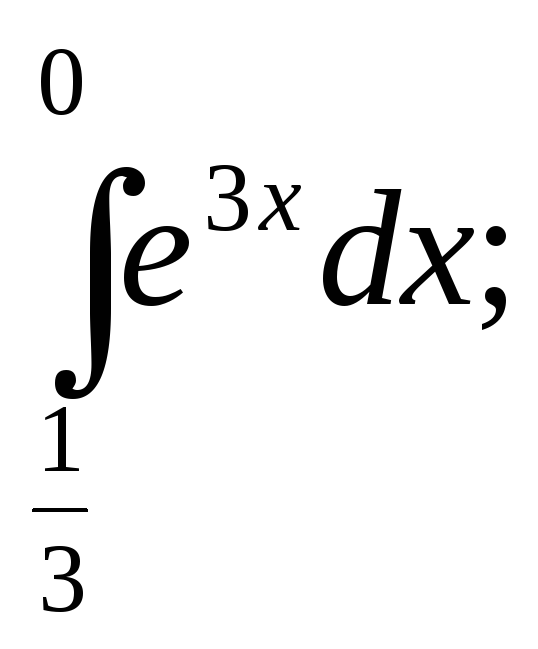
13.
![]() 18.
18.
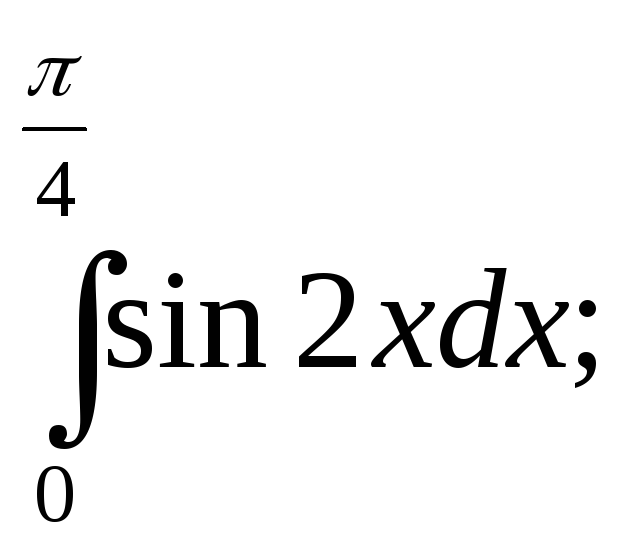
14.
![]() 19.
19.
![]()
15.
![]() 20.
20.
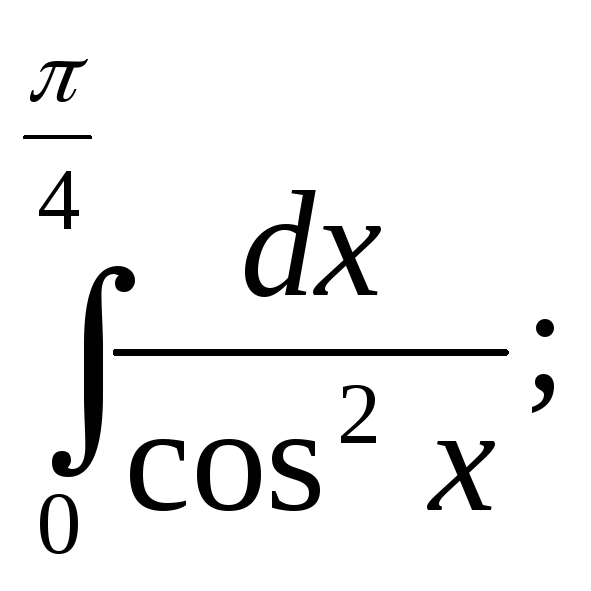
Вычислить площадь фигуры, ограниченной указанными ниже линиями. Сделать чертеж.
21. y = x2, y = x+2;
22. y = x2-3, y = -2x;
23. y = x2-4x, y = -3;
24. y = 2x2-2x-3, y =x2 +3x+3;
25. y = 3x2+2x+1, y =2x2 +3x+3;
26. y = x2, y =4x-3;
27. y = x2-6, y =5x;
28. y = x2+2x, y 3;
29. y = x2-2x-3, y =2x2 –x-5;
30. y = 2x2, y =-x2+3.
V. Дифференциальные уравнения.
Для решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами вида
![]() (1)
(1)
Составляют характеристическое квадратное уравнение
![]() (2)
(2)
Которое получается из уравнения (1) заменой в нем производных искомой функции у соответствующими степенями r, причем сама функция у заменяется единицей. Тогда общее решение уравнения (1) строится в зависимости от дискриминанта Д квадратного уравнения (2).
Практика показывает, что наиболее трудным является случай Д<0, когда уравнение (2) имеет пару сопряженных комплексных корней
![]() где
где
![]() а α и β – действительные числа, причем
β>0. Общее решение в этом случае таково:
а α и β – действительные числа, причем
β>0. Общее решение в этом случае таково:
![]()
Задача 1. Найти α и β, если корни уравнения (2) имеют вид:
![]()
Решение:
Преобразуем выражения для
![]() и
и
![]() :
:
![]()
Нетрудно
видеть, что
![]()
В
частном случае, если
![]()
Задача
2.
Найти частное решение уравнения
![]() ,
удовлетворяющее начальным условиям
у(0)=0,
,
удовлетворяющее начальным условиям
у(0)=0,
![]()
Решение:
Данная задача с начальными условиями
носит название задачи Коши. Составим
характеристическое уравнение: r2-1=0.
Его решениями являются
![]() Общее решение уравнения в этом случае
(Д>0) находится по формуле
Общее решение уравнения в этом случае
(Д>0) находится по формуле
![]() ,
т.е.
,
т.е.
![]() .
(3)
.
(3)
Найдем
![]() (4)
(4)
Подставим в уравнения (3) и (4) начальные условия:
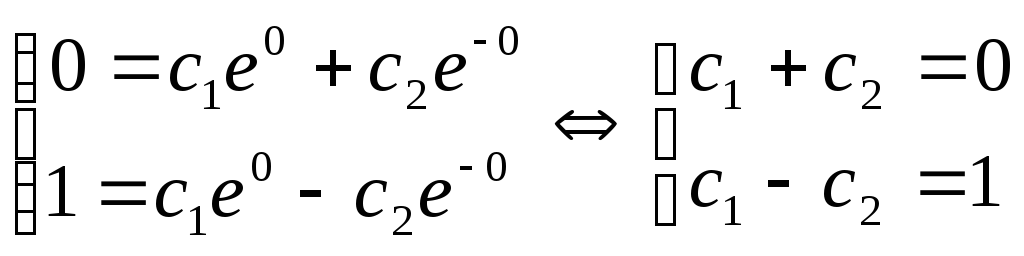
Решая
эту систему, получаем
![]() Найденные значения постоянных с1
и с2
подставляем
в общее решение (3) и получаем искомое
решение
Найденные значения постоянных с1
и с2
подставляем
в общее решение (3) и получаем искомое
решение
![]() или
или
![]()
