III. Введение в математический анализ. Дифференциальное исчисление функции.

Тема 1. Введение в математический анализ. Область определения функции совпадает с ОДЗ (областью допустимых значений) правой части , т.е. с множеством всех значений х, при которых вычисляется.

Задача 1. Найти область определения функции

Решение. Первая часть вычисляется при всех значениях х, для которых подкоренное выражение неотрицательно. Поэтому область определения D(y) будет найдена из условия . Решая это неравенство, получаем , т.е.

При анализе функции полезно проверить, обладает ли она свойством четности или нечетности. Наличие этих свойств позволяет упростить построение графика функции. Достаточно построить график функции для . Тогда для четной функции часть графика для получается симметричным отображением построенного графика относительно оси Оу, а для нечетной – относительно начала координат.

Задача 2. Выяснить, обладают ли данные функции свойством четности или нечетности:

а) б) .

Решение.

а) .

Итак, и, следовательно, функция является четной.

б), т.е. и, следовательно, функция у(х) является нечетной. Здесь использовано свойство модуля (абсолютной величины) числа: .

Вопросы для самопроверки:

1. Что называется функцией?

2. Какие способы задания функции Вы знаете?

3. Какая функция называется четной, а какая нечетной?

Тема 2. Пределы

Функция называется непрерывной в точке , если имеет место равенство:

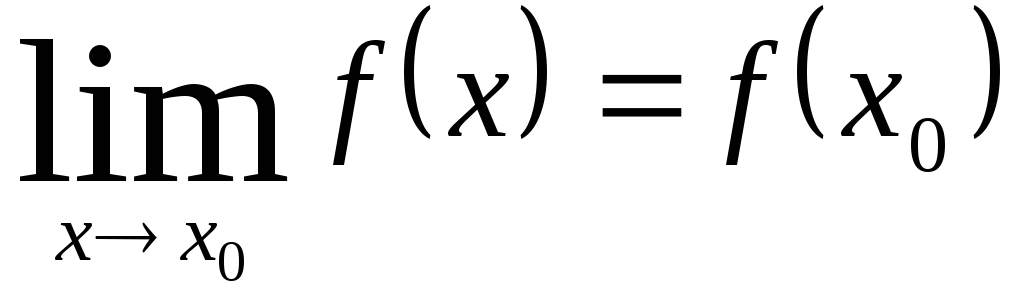(1), которое помогает очень просто находить пределы непрерывных функций. Для вычисления предела такой функции находят ее значение в предельной точке . К непрерывным относятся все элементарные функции, а также многочлены в любой точке их области определения.

Например,

;

;

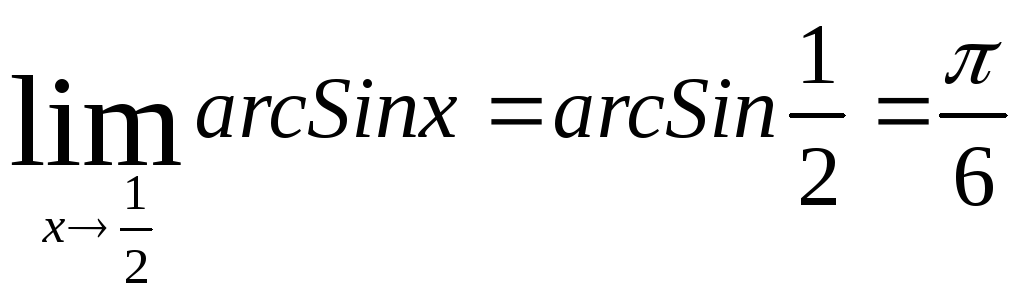Если равенство (1) не выполняется, то функция разрывна в точке .

Но, если не существует значение , это не означает, что не вычисляется предел функции при .

Задача 1. Найти

Решение:

Дробь при не вычисляется, причем и , т.е. дробь представляет собой отношение двух бесконечно малых функций (неопределенность вида ). Для вычисления предела дроби (раскрытия неопределенности) следует разложить и числитель, и знаменатель на множители и при наличии одинакового множителя, стремящегося к 0 при , дробь на этот множитель сократить: .

Для разложения на множители числителя необходимо вспомнить формулу , где и - действительные корни квадратного трехчлена, .

Для трехчлена , , , .

Поэтому .

Для преобразования будут такими:

;

.

Задача 2. Найти .

Решение:

При х=5 дробь не вычисляется, пределы числителя и знаменателя равны 0, т.е. имеем неопределенность вида . Для раскрытия неопределенности следует избавиться от конкретных иррациональностей в числителе и знаменателе, а при наличии общего множителя дробь на него сократить. Достигается это с помощью следующих тождественных преобразований для :

=.

Теперь .

Хорошо известен 1 замечательный предел: . Но часто аргументом синуса является функция , стремящаяся к 0 при . В этом случае .

Задача 3. Найти .

Решение: Дробь при х=0 не вычисляется , , имеем неопределенность вида . Преобразуем дробь следующим образом: .

.

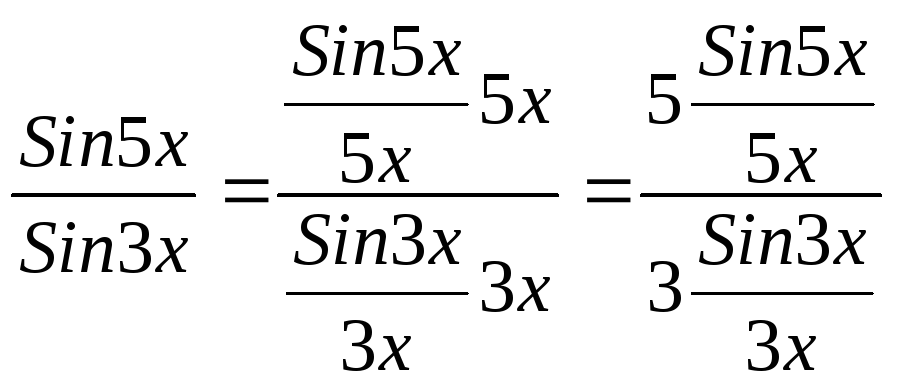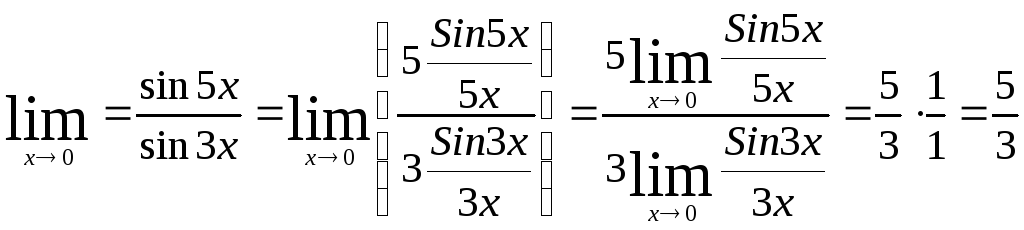Следует отметить, что если функция есть дробь, числитель который при имеет предел, отличный от 0, а знаменатель, напротив, имеет пределом 0, то .

Задача 4. Найти .

Решение: , .

Следовательно, .

Задача 5. Найти .

Решение: При и числитель, и знаменатель – Бесконечно большие функции (неопределенность вида ). Для раскрытия неопределенности преобразуем дробь, разделив числитель на знаменатель на старшую степень , т.е. на :

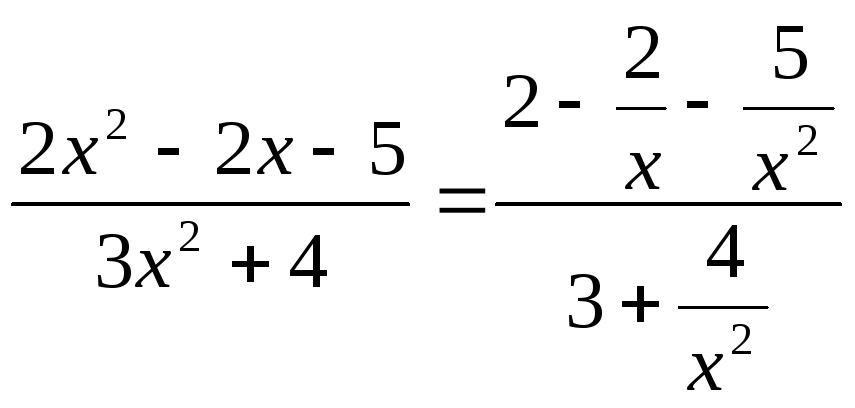. Теперь =

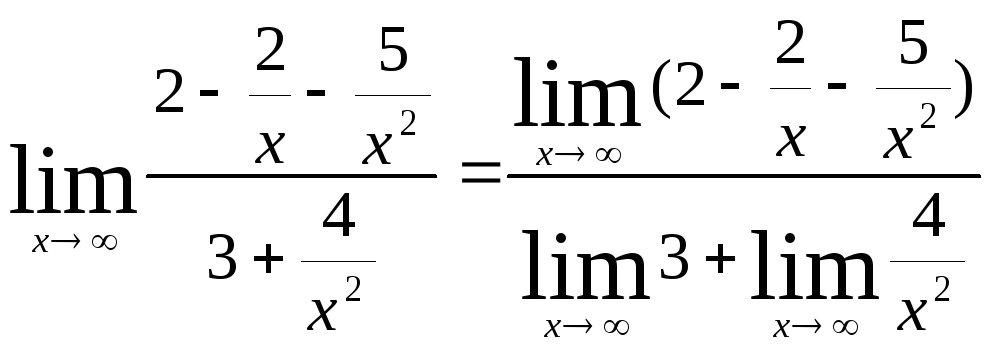Задача 6. Найти .

Решение: Имеем неопределенность вида . Разделим числитель и знаменатель на . Тогда:

.

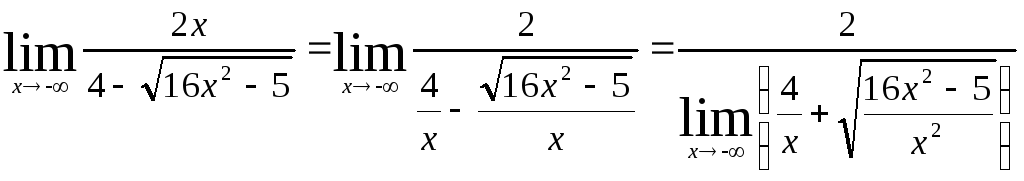
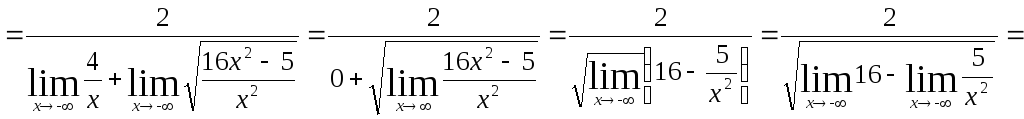
Здесь была использована формула: .

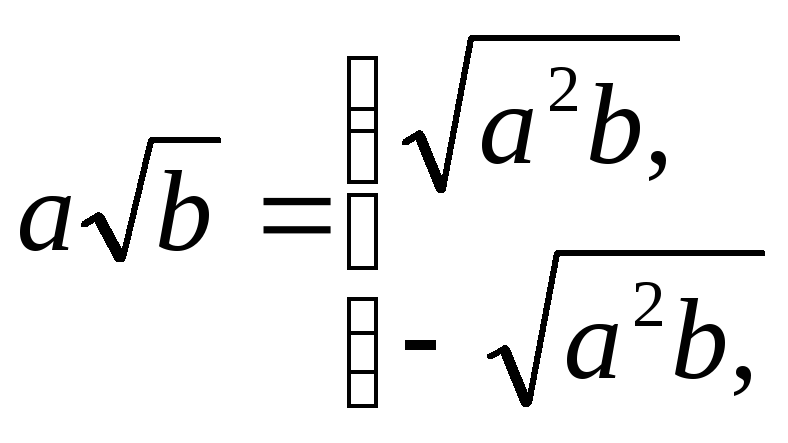
Задача7. Найти ,

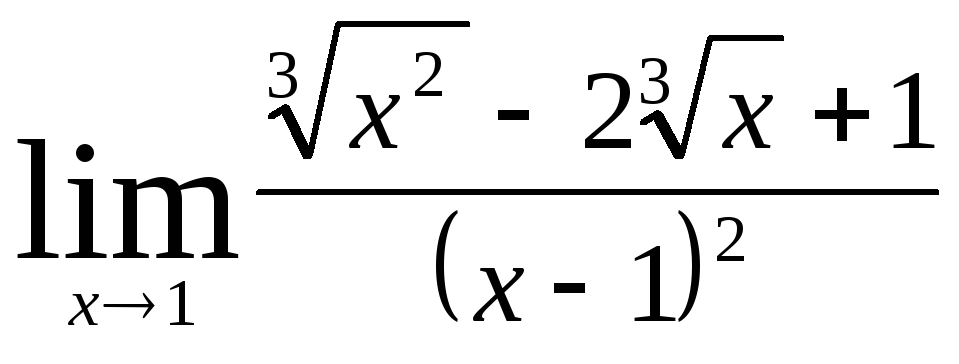Решение:

При и числитель, и знаменатель дроби стремятся к 0, т.е. имеем неопределенность вида . Для раскрытия неопределенности предварительно избавимся от иррациональности, сделав замену . Тогда , .

При . Теперь
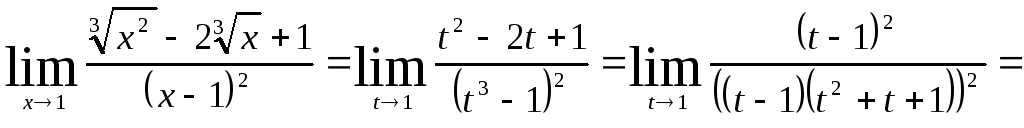