Индивидуальные задания Вариант №6

По курсу «Математические методы компьютерного моделирования физических процессов»

Для студентов КТАС, МИППС

Задача №1

Жидкость вытекает из резервуара через водослив прямоугольной формы. Получить, с помощью теории размерностей, структуру зависимости объемного расхода жидкости от высоты уровня ее в водосливе, ширины водослива ускорения свободного падения.

Задача№2

Скомканная бумажка массой 20 г брошена под углом 45 к горизонту. При полете она встречает силу сопротивления . Где А=0.1 Нс/м, В=2·10^-4 Нс²/м². Найдите траекторию. Сравните с траекторией в отсутствие силы сопротивления.

Задача№3

Привести уравнение движения спутника планеты к безразмерному виду. Составить функцию u=planet(u), которая бы выводила анимацию спутника и его траекторию. Предусмотрите вызов диалога для выхода из функции по нажатию клавиши мыши (questdlg). Данная функция должна использовать на входе начальный вектор состояния и возвращать на выходе текущий вектор состояния.

Исследуйте, как изменится траектория, если спутник получит небольшой толчок в направлении движения движению, или в противоположную сторону?

Задача№4

Сколько времени падает карандаш длиной 18 см, поставленный на острие. Предположим, что начальное отклонение равно1°, а острие не скользит. Как распространить полученный результат на стержень произвольной длины.

Задача№5

В механике чаще всего автоколебания возникают в тех случаях, когда осциллятор возбуждается за счет трения о равномерно движущийся предмет (скрип открываемой двери, колебания струны смычковых музыкальных инструментов). Простейшая модель была предложена Ван-дер-Полем, где 1-равномерно движущаяся со скоростью V₀ лента транспортера, 2-груз, 3-пружина.

Покажите, что при определенных условиях система придет в колебания. Нарисуйте график x(t) и фазовый портрет v(x).

Указание: считать, что сила, действующая на тело со стороны транспортера равна

F_тр=sign(u)*(f₀+b*abs(u)), где u=v₀-v– относительная скорость, .

Задача№6

Построить поле потенциала, созданного зарядами одинаковой величины и разных знаков, расположенных в вершинах квадрата так, что на каждой из сторон расположены разноименные заряды. С помощью функции contour3 изобразить это поле в виде линий уровня.

Задача№7

Заряженные частицы (главным образом протоны) летят от Солнца к Земле и попадают в неоднородное поле Земли , которое можно приближенно считать полем диполя с моментом p=2.510²² Ам². Постройте траекторию частицы. Напряженность магнитного диполя равна

Индивидуальные задания Вариант №7

По курсу «Математические методы компьютерного моделирования физических процессов»

Для студентов КТАС, МИППС

Задача №1

С помощью теории размерностей определите структура взаимосвязи параметров, описывающих работу вентилятора: диаметр винта , производительность (объемный расход) , плотность среды , напор (избыточное давление) , мощность , частота вращения . Как зависят от частоты вращения следующие величины: , , ?

Задача№2

Как изменяются дальность и время полета скомканной бумажки массой 20 г в зависимости от угла бросания? Начальная скорость равна 20 м/с, сила трения , где В=2·10^-4 Нс²/м²

Задача№3

Привести уравнение движения планеты к безразмерному виду. Составить функцию, которая бы выводила анимацию планеты и ее траекторию. Предусмотрите вызов диалога для выхода из функции по нажатию клавиши мыши (questdlg).

Исследуйте, как изменится траектория, если на планету действует сила притяжения, немного отличающаяся от закона обратных квадратов: . Может ли такое наблюдаться на практике?

Задача№4

Начертите график зависимости угла и угловой скорости от времени падающего дерева высотой 15 м. Начальное отклонение от вертикали 10°, 5°,1°.

Задача№5

Математической моделью типичной автоколебательной системы, лампового генератора, является генератор Ван-дер-Поля, который описывается следующим нелинейным дифференциальным уравнением: . Здесь q- безразмерный заряд на конденсаторе, μ-параметр настройки. Построить графики и фазовые траектории, начинающиеся с малых и больших значений (q₀<<1, q₀ >2). Убедитесь в существовании предельного цикла. Какое практическое значение имеет это обстоятельство. Эксперимент проведите для различных значений μ (<1, >1, 10, 100, 1000).

Указание: Для больших значений μ, система становится жесткой и, для обеспечения эффективности вычислительного процесса, следует использовать солвер ode15s и подключить функцию, вычисляющую якобиан системы.

Задача№6

Три заряда q,q и –2q расположены в вершинах равнобедренного треугольника. Начертить силовые линии электрического поля и эквипотенциальные уровни электрического поля. Произвести измерение потенциала в точке и, пользуясь теорией подобия, пересчитать на случай

Задача№7

Согласно принципу Ферма, луч света выбирает путь, для которого время распространения между двумя точками минимально. Если показатель преломления , то данный принцип приводит к следующему дифференциальному уравнению: .

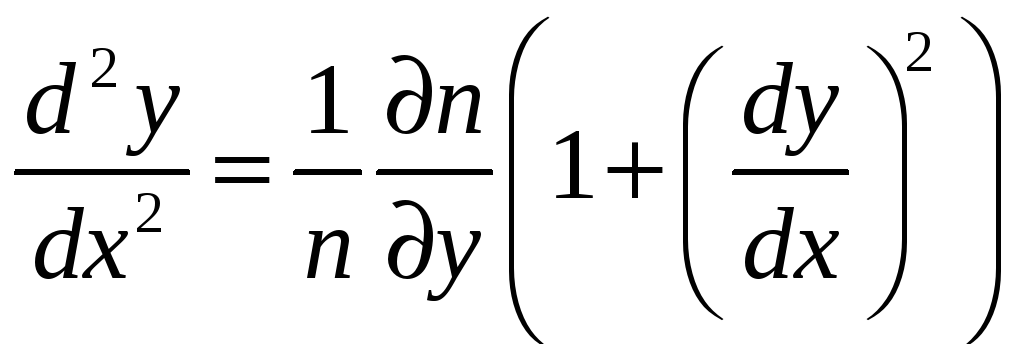Показатель преломления равен , где - диэлектрическая восприимчивость. Полагая, что пропорционален плотности воздуха, которая зависит от высоты согласно барометрической формуле Лапласа, где h₀ =8∙10³ м, и показатель преломления на нулевой высоте равен n₀ =1,0004, построить траекторию луча, входящего в глаз наблюдателя под углом 10° к горизонту. Под каким углом находится звезда, испускающая этот луч?

Указание: Согласно принципу Ферма, луч света выбирает путь, для которого время распространения между двумя точками минимально. Если показатель преломления , то данный принцип приводит к следующему дифференциальному уравнению: , позволяющему найти траекторию луча.