Растяжение и сжатие. Удлинения и деформации при растяжении и сжатии

Растяжением будем называть такое нагружение стержня, когда в поперечных сечениях возникает лишь один внутренний силовой фактор – нормальная сила.

Для того чтобы возникло растяжение необходимо, чтобы внешние силы, приложенные по торцам стержня, были статически эквивалентны сосредоточенной силе, приложенной по оси стержня.

Схематизируя силы, приложенные к стержню, мы используем принцип Сен-Венана, который в данном конкретном случае примет следующий вид: “Способ приложения нагрузки не сказывается в сечениях достаточно удаленных от места приложения нагрузки”.

Н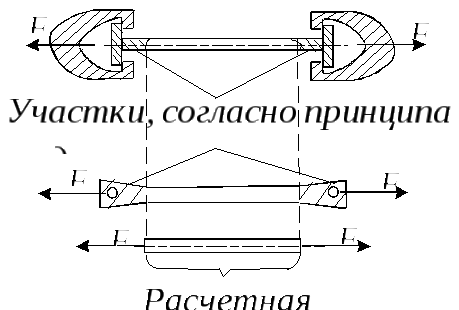апример, стержень одной и той же длины и сечения загружается разным образом. В первом случае имеется закладная головка, которая помещена в захваты испытательной машины, во втором случае она представляет собой равнодействующую давления со стороны болта или заклепки. Безусловно, что характер распределения напряжений в месте передачи нагрузки, совершенно различный и весьма сложный. Однако, на расстояниях равных примерно характерному размеру поперечного сечения, индивидуальности в передачи нагрузки не сказываются, и для обоих случаев может быть принята одна и та же расчетная схема: Стержень загружен по торцам сосредоточенными силами, направленными по оси.

Параллельно с растяжением мы будем рассматривать и случай сжатия, отличая его от растяжения лишь знаком нормальной силы и напряжения. Но в данной лекции мы будем рассматривать сжатие коротких стержней, длина которых не превышает нескольких размеров поперечного сечения.

13)

Коэффициенты запаса прочности и допускаемые напряжения

Состояния, при которых происходят коренные изменения механического состояния материала в точке, называется предельным.

Различают два предельных состояния:

1) Переход материала в пластическое состояние, т.е. появление значительных остаточных деформаций.

2) Разрушение. Т.е. рост трещин и распадение на части.

Соответственно сказанному, оценивая состояние конструкции, различают два коэффициента запаса:

а) Коэффициент запаса по текучестигде

- предел текучести;

- максимальное напряжение, возникающее в конструкции.

По данному коэффициенту оцениваются конструкции, выполненные из достаточно пластичных материалов.

б) Если материал конструкции хрупок и обладает незначительными пластическими свойствами, то прибегают к коэффициенту запаса по разрушению где

- предел прочности или временное сопротивление.

Иногда коэффициенты запаса выступают в другом качестве: в роли нормативных заданных величин, с помощью которых определяются так называемые допускаемые напряжения:

Допускаемое напряжение;

а) для пластичных материалов определяется

б) Для хрупких материалов

Расчет по методу допускаемых напряжений состоит в обеспечении условия: , называется условием прочности.

14)

Закон Гука при растяжении и сжатии

Как уже упоминалось ранее, между напряжениями и деформациями существует связь, которая может быть установлена лишь экспериментальным путем.

Б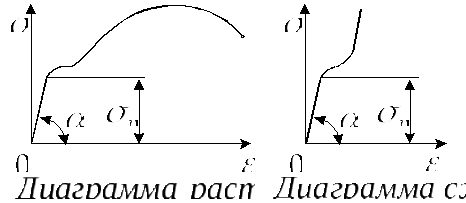ольшинство твердых тел, при сравнительно небольших нагрузках, обнаруживают свойство однозначной зависимости между напряжениями и деформациями (или между силами и перемещениями).

Например, если вспомнить известные нам из курса лабораторных работ диаграммы растяжения и сжатия малоуглеродистой стали, то можно заметить, что вплоть до значений напряжения равного - предела пропорциональности зависимость между напряжениями и деформациями близка к линейной.

Подобная картина наблюдается и у других сталей, а также, может быть менее отчетливо, у других материалов. Данный экспериментальный факт позволяет принять простейший из упругих законов – закон Гука, т.е. закон линейной упругости:

Напряжения пропорциональны деформациям

Коэффициент пропорциональности между напряжениями и деформациями называется модулем упругости первого рода (модулем Юнга). Модуль упругости определяется опытным путем и служит мерой жесткости материала. Геометрический смысл - угловой коэффициент прямолинейного начального участка диаграммы материала.

Модуль упругости для некоторых, часто применяемых материалов, имеет приблизительно следующие значения.

Сталь:; Медь: ;

Дерево: ; Каучук:

Отметим еще раз, что свойство упругости, в частности линей-

ной упругости, относительно. Уместно говорить не о упругих и неупругих материалах, а о упругом и неупругом состоянии материала.

Если в (3) выразить по формуле (2) и учесть (1), то получим закон Гука в форме, позволяющей находить удлинения.

Величину называют жесткостью при растяжении-сжатии. Закон (4) можно сформулировать следующим образом: удлинение стержня прямо пропорционально нормальной силе и длине стержня и обратно пропорционально жесткости при растяжении-сжатии.

По формуле (4) можно определять удлинения только в том

случае, если нормальная сила и поперечное сечение постоянны по

длине стержня, т.е. если напряженное состояние однородно.

Если нормальная сила и поперечное сечение меняются по длине ступенчато, то стержень надо разбить на участки, так чтобы в пределах каждого участка и были постоянны, определить удлинение каждого из участков и тогда полное удлинение стержня будет равняться алгебраической сумме, (знак определяется знаком ) удлинений участков.

Е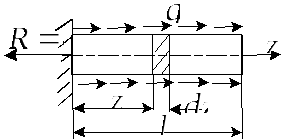сли же напряженное состояние в стержне неоднородно, то выделив малый элемент длиной определим его удлинение

, Здесь и рассматривается как функции z. Полное удлинение стержня будет равно:

15)