6.7. Тригонометричні підстановки.

Інтеграли виду , , приводять до інтегралів від раціональної відносно і функції за допомогою відповідної тригонометричної підстановки.

,

,

.

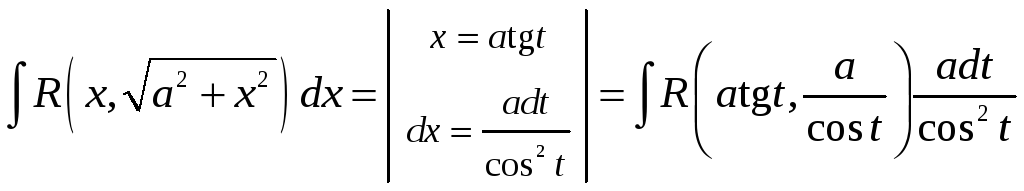Подальші обчислення отриманих інтегралів аналогічні обчисленням показаним в прикладах розд. 6.6.

Приклад 6.14. Обчислити невизначений інтеграл:

.

Розв’язок. Зробимо заміну змінної . Тоді

Повертаючись до змінної величини за допомогою підстановки , остаточно одержимо:

.

Л і т е р а т у р а: [4, гл. 6, §2, п. 3; 6, гл. Х, § 13].

6.8. Інтеграли, що не виражаються через елементарні функції.

Наведені способи обчислення невизначених інтегралів, природно, не вичерпують існуючих методів обчислення інтегралів. Є численна література з цього питання, до якої можна звернутися при необхідності.

Слід мати на увазі, що дуже часто інтеграли від елементарних функцій не виражаються через елементарні функції. До таких інтегралів відносяться, наприклад,

, , , ,

і багато інших. Найбільш важливі з них, що мають застосування у техніці і природознавстві, носять спеціальні назви. Їхні властивості добре вивчені і для них складені таблиці, тому у деяких випадках з ними можна працювати у той же спосіб, що й з елементарними функціями.

Питання для самоперевірки.

1. Що називається первісною функцією?

2. Що називається невизначеним інтегралом?

3. Яка взаємовідповідність існує між операціями диференціювання та інтегрування?

4. Випишіть таблицю основних інтегралів. Зіставте її з таблицею похідних.

5. Які правила інтегрування вам відомі?

6. Виведіть формулу інтегрування частинами.

7. У чому полягає застосування цієї формули? Наведіть приклади.

8. Виведіть формулу заміни змінної у інтегралі. Наведіть приклади.

9. Як інтегрують найпростіші раціональні дроби?

10. Сформулюйте методику обчислення невизначених інтегралів від раціональних функцій. Наведіть приклади.

11. Які інтеграли можна звести до інтегралів від раціональної функції? Які при цьому використовують підстановки?

12. Як обчислюють інтеграли що містять ірраціональні функції? Наведіть приклади.

13. Як обчислюють інтеграли, що містять тригонометричні функції? Наведіть приклади.

14. До яких інтегралів можна застосувати тригонометричні підстановки?

15. Чи всі інтеграли від елементарних функцій виражаються через елементарні функції?

Л і т е р а т у р а: [5, гл. 5, § 5.2; 6, гл. Х, § 14].

93