6.4. Інтеграли від раціональних функцій.

Як було показано вище, інтеграл від многочлена дорівнює сумі інтегралів від степеневих функцій, тобто сумі табличних інтегралів.

При інтегруванні раціонального дробу (відношення многочленів ) попередньо його треба подати у вигляді суми многочлена (цілої частини, якщо ) й найпростіших дробів. Процедура розкладання дробу на найпростіші викладена у темі 5 (розд 5.2).

Найпростіші дроби класифікують в залежності від характеру коренів знаменника .

1) Інтеграли від найпростіших дробів, що відповідають дійсним кореням знаменника, знаходять безпосередньо за допомогою таблиці інтегралів.

2) Інтеграли від дробу , що відповідає парі комплексно спряжених коренів знаменника , обчислюють у такий спосіб:

а) виділяють повний квадрат у знаменнику

, де ;

б) роблять підстановку що зводить інтеграл до лінійної комбінації двох інтегралів, один з яких приводять до арктангенсу, а другий  до логарифму.

Проілюструємо обчислення таким прикладом:

Приклад 6.4. Знайти невизначений інтеграл:

.

Розв’язок. Дріб неправильний, виділяємо цілу частину:

.

Правильний дріб розкладаємо на суму найпростіших дробів:

.

Приводимо суму дробів до спільного знаменника і порівнюємо чисельники:

.

Прирівнюємо коефіцієнти при однакових степенях змінної в обидвих частинах рівності і знаходимо значення , , :

Тоді

Звідси отримуємо:

Приклад 6.5. Знайти невизначений інтеграл:

.

Розв’язок. Розкладемо підінтегральний вираз на найпростіші дроби:

;

;

;

.

Виділяємо повний квадрат у знаменнику:

;

Звідси отримуємо:

.

Л і т е р а т у р а: [4, гл. 6, § 2, п. 1; 5, гл. 5, § 5.6; 6, гл. Х, § 7-9].

6.5. Інтеграли, що зводяться до інтегралів від раціональних функцій.

Підстановка зводить інтеграл , де через позначено раціональну функцію, до інтегралу від раціональної функції

.

Приклад 6.6. Обчислити невизначений інтеграл:

.

Розв’язок.

Інтеграли виду також зводять до інтегралів від раціональної функції:

.

Тут  раціональна функція від і .

Аналогічно обчислюють інтеграли виду за допомогою підстановки

Приклад 6.7. Обчислити невизначений інтеграл:

.

Розв’язок.

Інші типи інтегралів, що містять радикали й зводяться до інтегралів від раціональної функції, можна знайти у рекомендованій літературі [5; 6].

Л і т е р а т у р а: [4, гл. 6, § 2, п. 3; 5, гл. 5, § 5.7; 6, гл. Х, § 10].

6.6. Інтеграли, що містять тригонометричні функції.

а) Інтеграли виду , , обчислюють з використанням тригонометричних співвідношень

(6.3)

Зокрема,

, . (6.4)

Приклад 6.8. Обчислити невизначений інтеграл: .

Розв’язок.

б) Інтеграли виду , де , можна обчислити з використанням тригонометричних співвідношень (6.3) і (6.4), знижуючи степінь тригонометричних функцій.

Приклад 6.9. Обчислити невизначений інтеграл: .

Розв’язок.

Якщо хоча б одно з чисел і не парне, то можна застосувати підстановку або .

Приклад 6.10. Обчислити невизначений інтеграл: .

Розв’язок.

Вказана підстановка може бути використана і для інтегралів більш загального виду.

в) Інтеграли виду в загальному випадку можна звести до інтегралів від раціональної функції за допомогою універсальної підстановки , .

Дійсно,

,

,

, ,

що дає

.

Універсальна підстановка часто спричиняє громіздкі викладки, у деяких випадках обчислення можна провести за допомогою інших підстановок, що призводять до більш простих обчислень:

1. Якщо функція 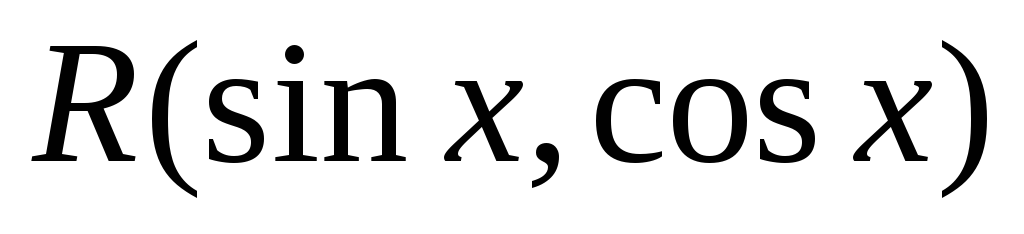непарна відносно , тобто , то доцільна підстановка .

2. Якщо то доцільна підстановка .

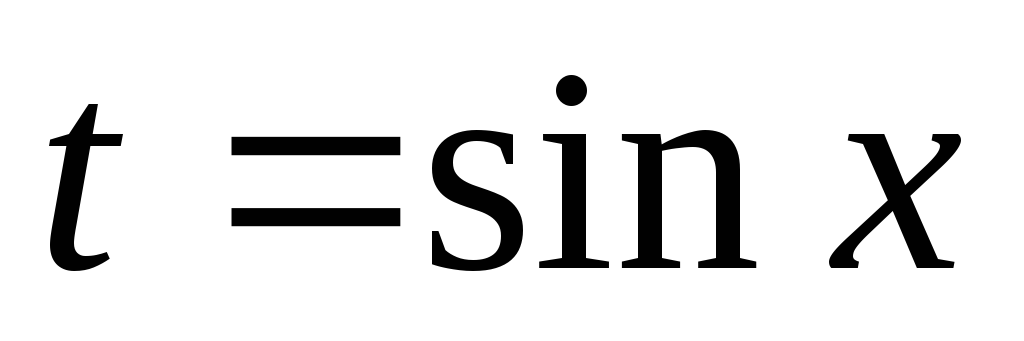3. Якщо функція не змінює свого значення при одночасній зміні знаків обох аргументів, тобто то ефективна підстановка , або .

У першому випадку функцію можна перетворити у функцію виду , у другому випадку  у функцію , у третьому випадку  у функцію .

Прослідкуйте у нижче наведених прикладах, як застосовуються вказані підстановки.

Приклад 6.11. Обчислити невизначений інтеграл:

.

Розв’язок. Підінтегральний вираз змінює знак внаслідок заміни на . Таким чином

Приклад 6.12. Обчислити невизначений інтеграл:

.

Розв’язок. Підінтегральний вираз не змінює свого значення при одночасній зміні знаків у і у . Таким чином

Приклад 6.13. Обчислити невизначений інтеграл:

.

Розв’язок. Підінтегральний вираз не змінює свого значення при одночасній зміні знаків у і у . Таким чином

Л і т е р а т у р а: [4, гл. 6, § 2, п. 2; 5, гл. 5, §5.7; 6, гл. Х].