
- •6.1. Означення та властивості невизначеного інтеграла.
- •6.2. Інтегрування частинами.
- •6.3. Іінтегрування заміною змінної.
- •6.4. Інтеграли від раціональних функцій.
- •6.5. Інтеграли, що зводяться до інтегралів від раціональних функцій.
- •6.6. Інтеграли, що містять тригонометричні функції.
- •6.7. Тригонометричні підстановки.
- •6.8. Інтеграли, що не виражаються через елементарні функції.
Т е м а 6. НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
У багатьох галузях науки і техніки доводиться розв’язувати задачі про відновлення функції за відомою її похідною, тобто задачу, обернену до основної задачі диференціального числення.
6.1. Означення та властивості невизначеного інтеграла.
Треба
знати, що функція
![]() у даному проміжку
у даному проміжку
![]() називається первісною функцією для
функції
називається первісною функцією для
функції
![]() або, коротше, первісною функції
або, коротше, первісною функції
![]() ,
якщо на всьому проміжку
,
якщо на всьому проміжку
![]() функція
функція
![]() є похідною функції
є похідною функції
![]() ,
тобто
,
тобто
![]() .
.
Будь-яка
первісна для функції
![]() може бути подана сумою, тобто
може бути подана сумою, тобто
![]() ,
де
,
де
![]()
довільна
стала (константа).
довільна
стала (константа).
Сукупність
усіх первісних функцій
![]() на проміжку
на проміжку
![]() називається невизначеним інтегралом
від функції
називається невизначеним інтегралом
від функції
![]() і позначається
і позначається
![]() .
.
Слід звернути увагу на властивості невизначеного інтеграла:
-
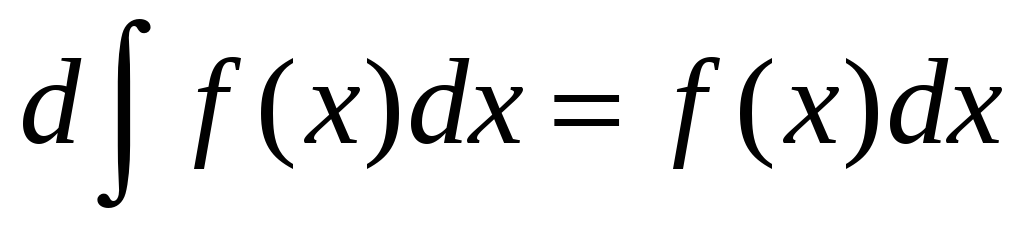 ,
тобто знаки диференціала
,
тобто знаки диференціала
 і
інтеграла
і
інтеграла
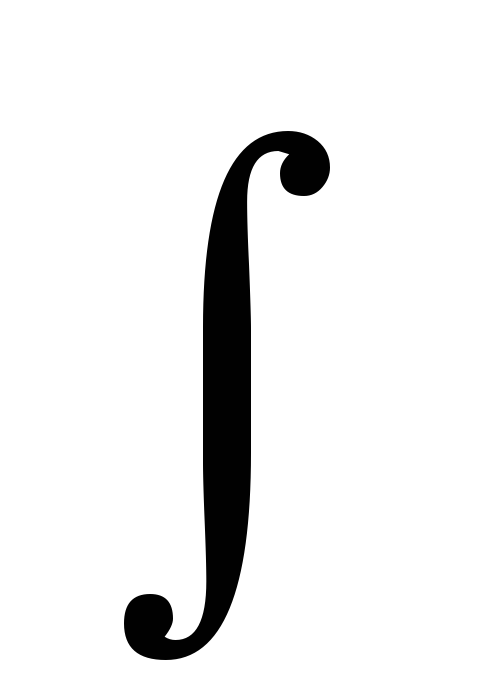 взаємно скорочуються, або
взаємно скорочуються, або
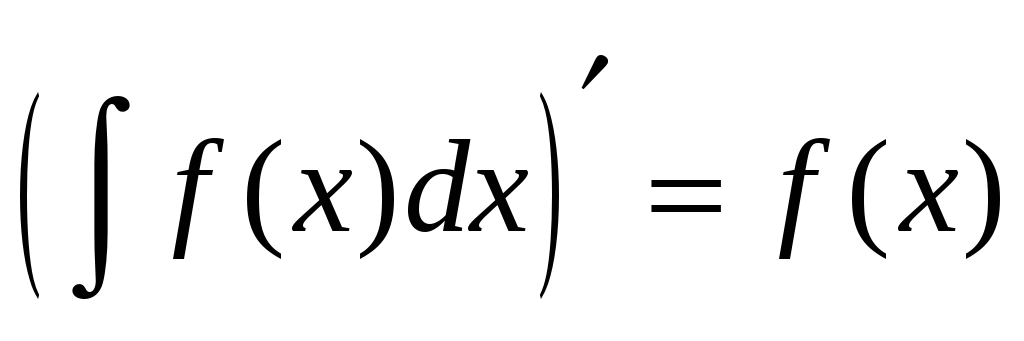 ;
; -

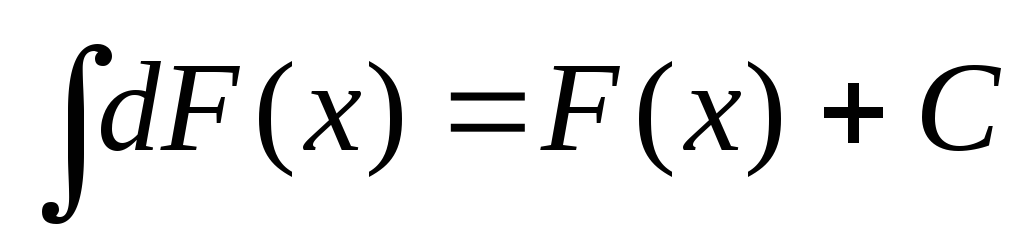 або
або
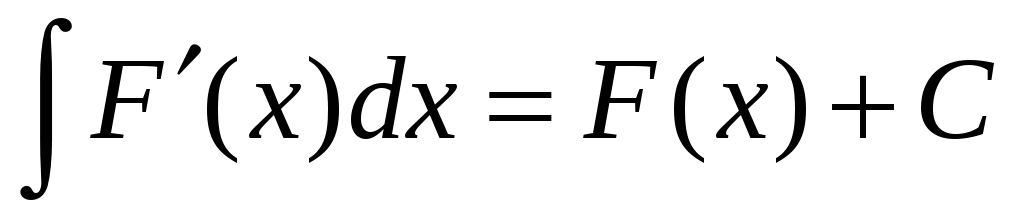 .
.
Знаходження
невизначеного інтеграла від функції
![]() називають інтегруванням функції
називають інтегруванням функції
![]() і, як видно з відзначених вище властивостей,
інтегрування і диференціювання є взаємно
оберненими операціями.
і, як видно з відзначених вище властивостей,
інтегрування і диференціювання є взаємно
оберненими операціями.
З таблиці похідних безпосередньо витікає таблиця інтегралів.
Таблиця інтегралів елементарних функцій
-
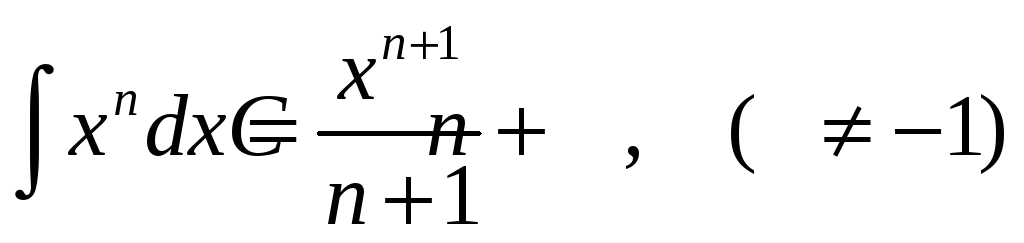 .
. -
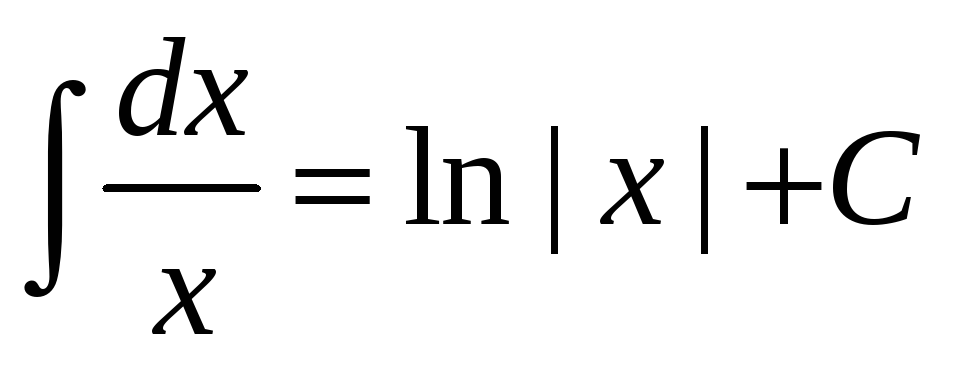 .
. -
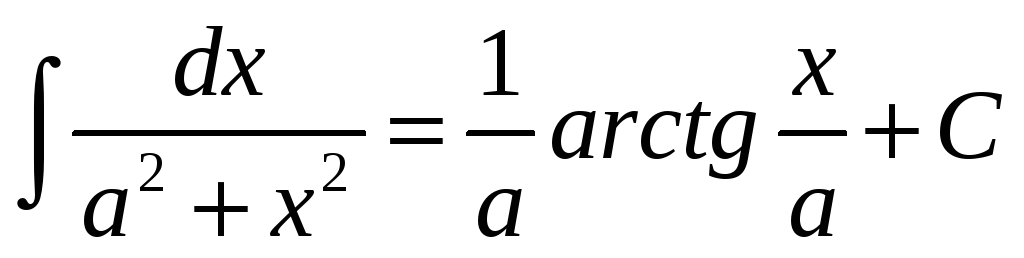 .
. -
 .
. -
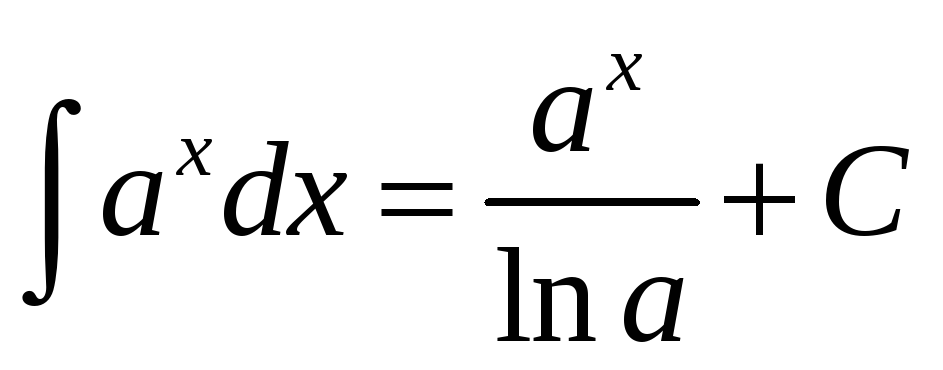 .
. -
 .
. -
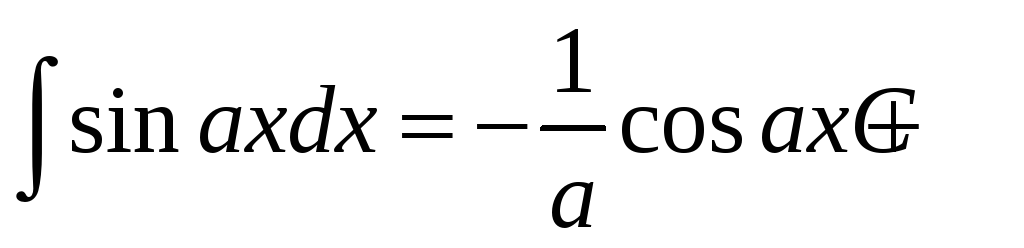 .
. -
 .
. -
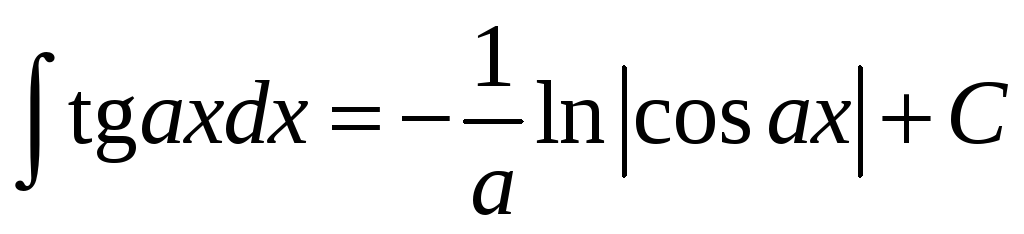 .
. -
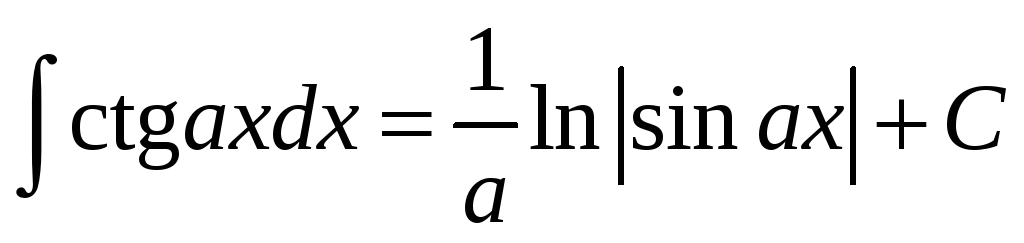 .
. -
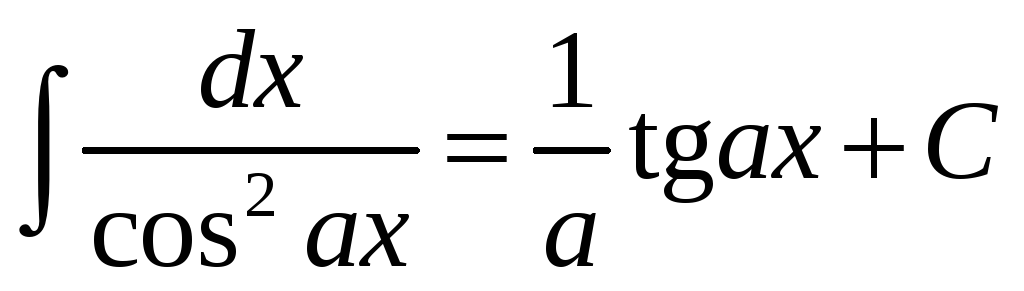 .
. -
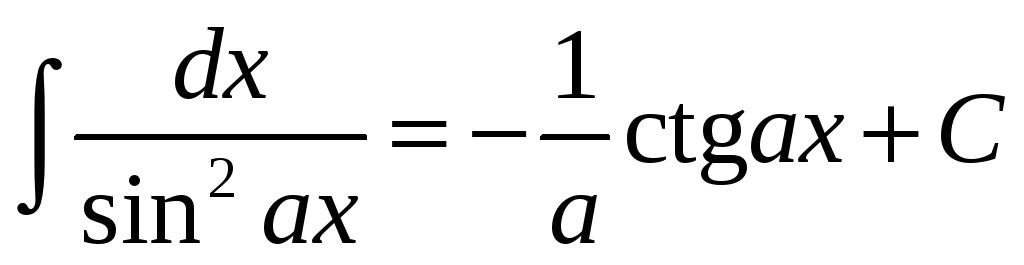 .
. -
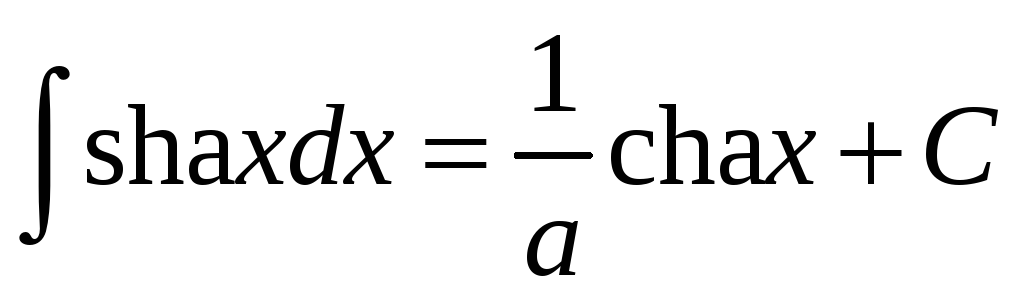 .
. -
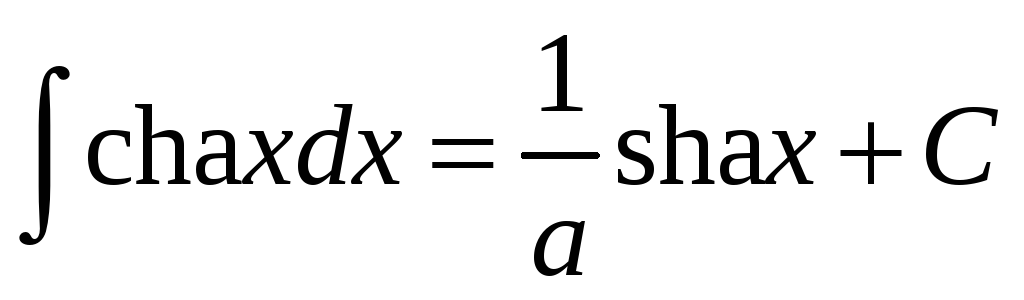 .
. -
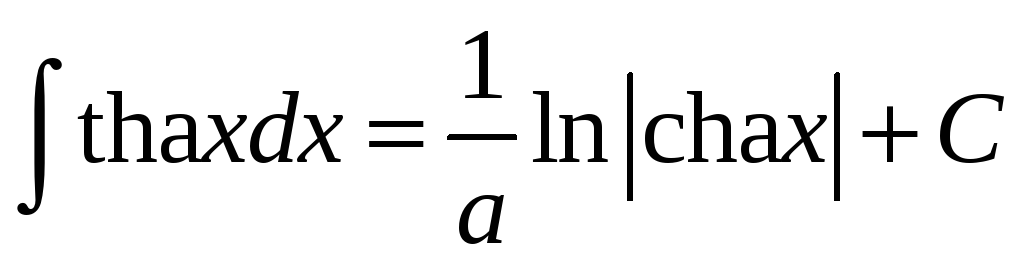 .
. -
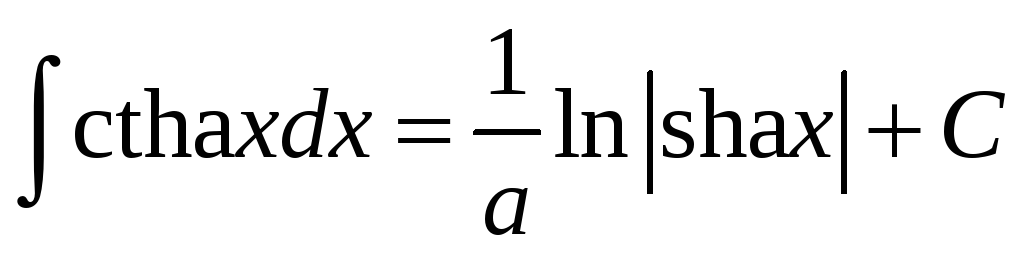 .
. -
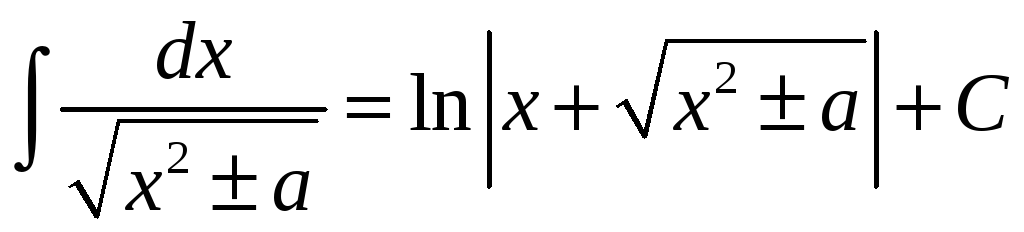 .
. -
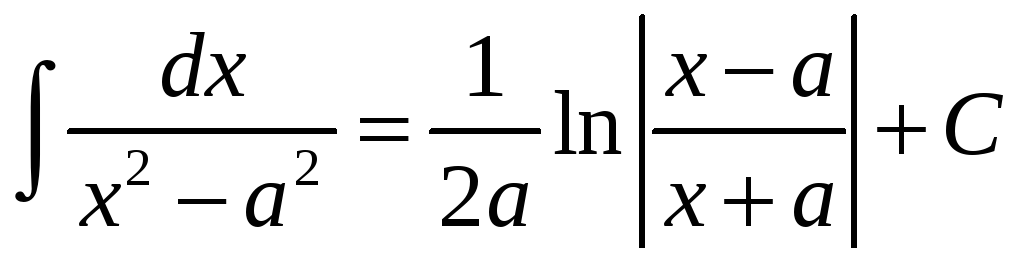 .
.
Диференціюванням перевірте вірність даної таблиці!
Можливості застосування таблиці інтегралів розширюються з використанням найпростіших правил інтегрування:
-
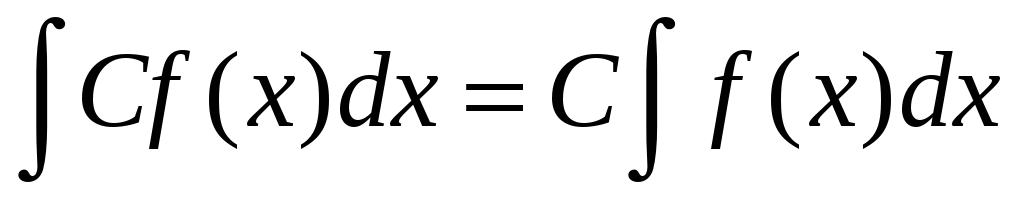 сталий
множник можна виносити з-під знака
інтеграла;
сталий
множник можна виносити з-під знака
інтеграла; -
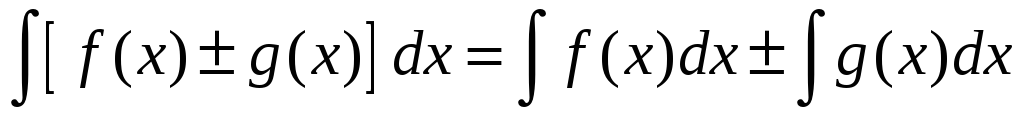 невизначений
інтеграл від суми (різниці) функції
дорівнює суми (різниці) інтегралів від
кожної функції окремо;
невизначений
інтеграл від суми (різниці) функції
дорівнює суми (різниці) інтегралів від
кожної функції окремо; -
Якщо
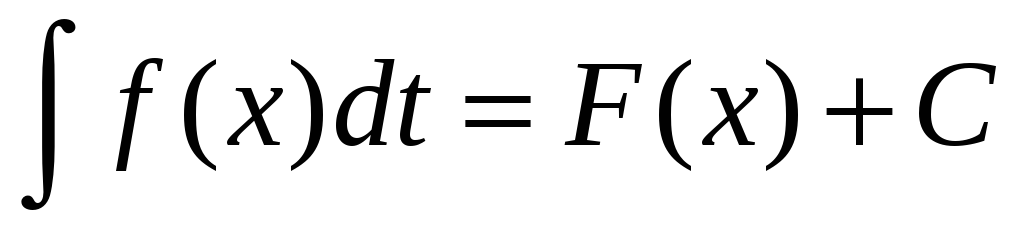 ,
то
,
то
![]() .
(6.1)
.
(6.1)
Диференціюванням переконайтеся у вірності наведених співвідношень.
Особливо
часто зустрічаються випадки, коли у
рівності (6.1)
![]() або
або
![]() :
:
![]() ,
,
![]() .
.
Приклад
6.1.
Обчислити
невизначений інтеграл
![]() .
.
Розв’язок. Використовуючи правила 1 та 2 і формулу 1 таблиці інтегралів, маємо:
![]() .
.
Слід відмітити два основних методи інтегрування, що дозволяють зводити інтеграли до більш простих інтегралів, які або є табличними, або легко до них зводяться. До цих методів належать інтегрування частинами та інтегрування заміною змінної.
На закінчення розділу наведемо деякі інтеграли, які можуть бути корисними у обчисленнях:
![]() ,
,
![]() ;
;
![]() ;
;
![]() .
.
Л і т е р а т у р а: [4, гл. 6, §1, п. 1; 5, гл. 5, §5.1; 6, гл. Х, § 1-3].
6.2. Інтегрування частинами.
Нехай
функції
![]() і
і
![]() мають неперервні похідні. Тоді має місце
рівність
мають неперервні похідні. Тоді має місце
рівність
![]() ,
,
або
![]() .
(6.2)
.
(6.2)
Докажіть ці рівності що передають правила інтегрування частинами.
Загальне
правило полягає у поданні підінтегральної
функції
![]() у вигляді добутку
у вигляді добутку
![]() ,
знаходженні первісної
,
знаходженні первісної
![]() для функції
для функції
![]() і застосуванні формули (6.2). Метод є
ефективним, якщо другий інтеграл у (6.2)
виявиться простішим ніж перший.
і застосуванні формули (6.2). Метод є
ефективним, якщо другий інтеграл у (6.2)
виявиться простішим ніж перший.
Для інтегралів типу
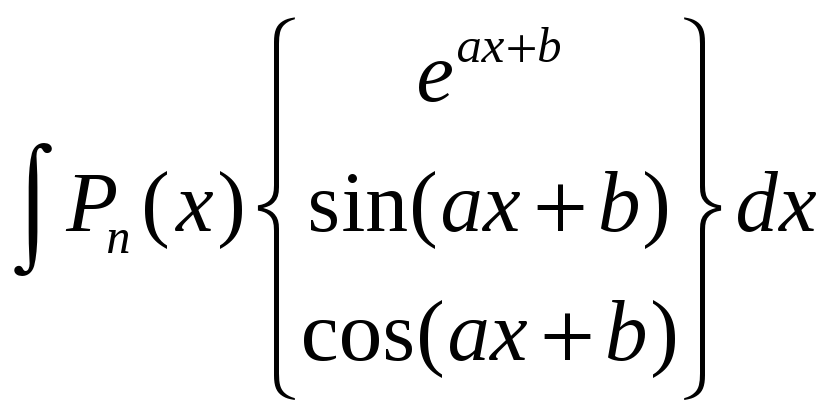
де
![]()
многочлен
многочлен
![]() го
степеня, слід прийняти
го
степеня, слід прийняти
![]()
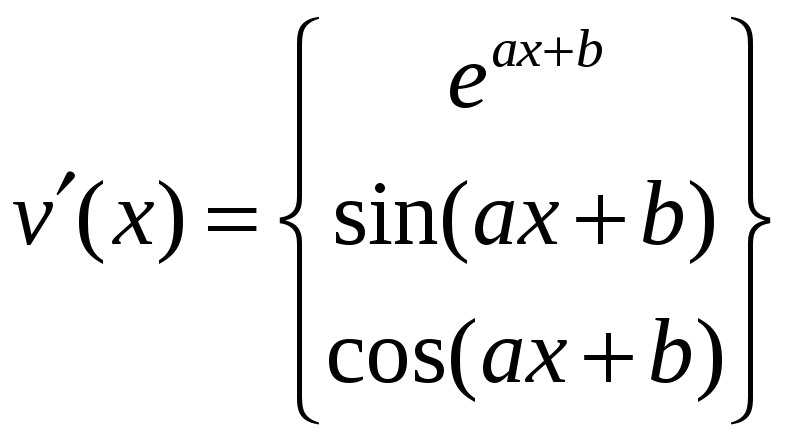
а для інтегралів типу
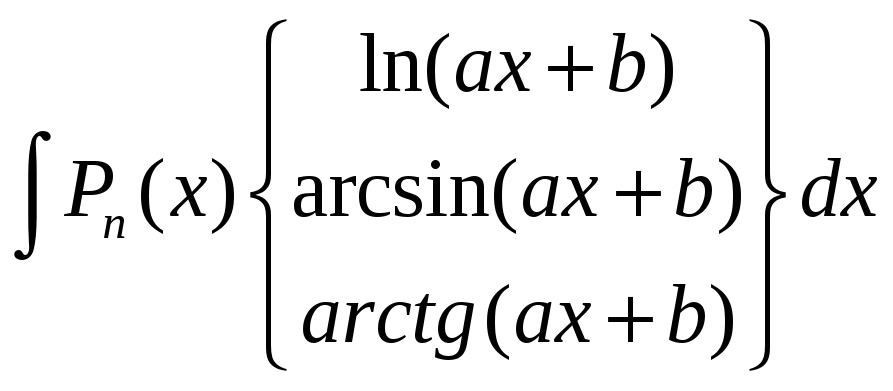 ,
,
слід прийняти
 ,
,
![]() .
.
Приклад
6.2.
Обчислити
невизначені інтеграли: 1)
![]() ;
2)
;
2)
![]() .
.
Розв’язок. Використовуючи правило інтегрування частинами, маємо:
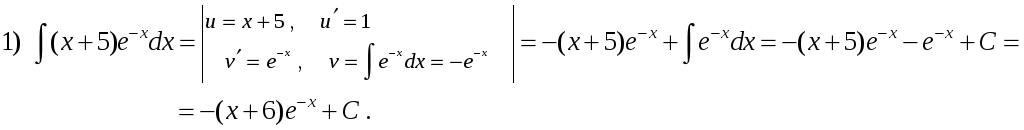
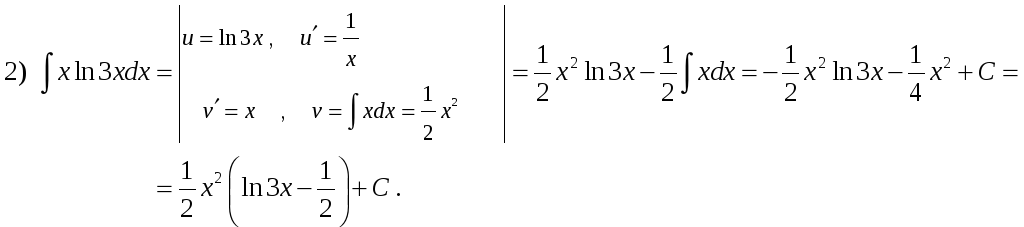
Запам’ятайте,
що довільну сталу
![]() при находжені
при находжені
![]() можна як це видно з прикладу 6.2, не писати.
можна як це видно з прикладу 6.2, не писати.
Л і т е р а т у р а: [4, гл. 6, § 1, п. 3; 5 гл. 5, § 5.2; 6, гл. Х, § 6].
6.3. Іінтегрування заміною змінної.
Нехай
![]()
первісна функції
первісна функції
![]() ,
функція
,
функція
![]() має неперервну похідну. Тоді
має неперервну похідну. Тоді
![]() ,
,
Прикладом заміни змінної є формула (6.1). Зверніть увагу, що після заміни змінної (підстановки) і інтегрування треба повернутися до старої змінної величини.
Можлива й інша форма заміни змінної:
![]()
де
![]()
первісна функції
первісна функції![]() ;
;
![]()
обернена функція до
обернена функція до
![]()
Вдалий вибір нової змінної істотно полегшує обчислення інтеграла.
Приклад 6.3. Обчислити невизначені інтеграли:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
Розв’язок. Використовуючи правило інтегрування частинами, маємо:
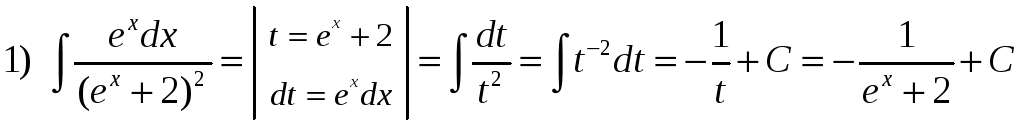 .
.
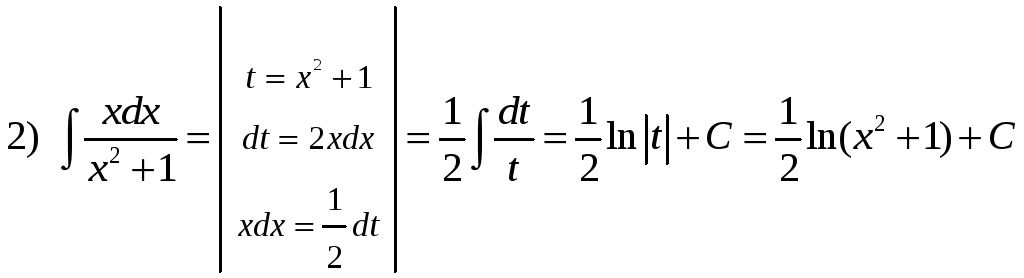 .
.
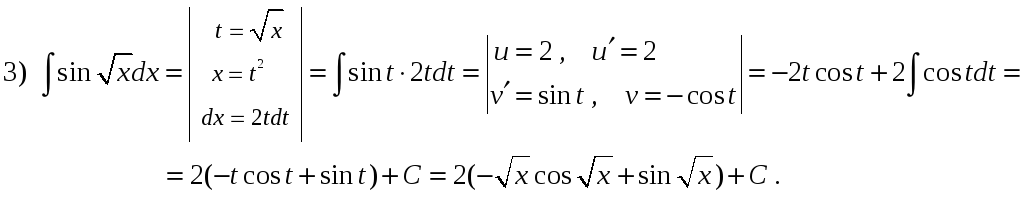
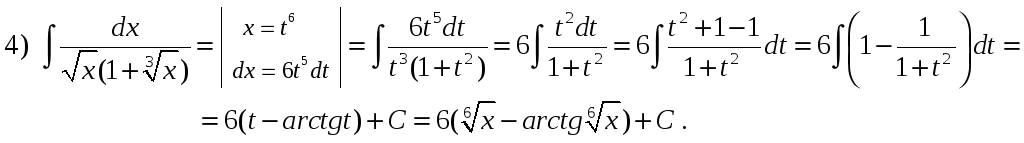
У
останньому інтегралі підстановка
![]() ,
обрана так, щоб усі корені “добувалися”.
Вибір вдалої підстановки вимагає певної
навички. Для деяких класів інтегралів
(див.
нижче)
можна вказати відповідні підстановки.
,
обрана так, щоб усі корені “добувалися”.
Вибір вдалої підстановки вимагає певної
навички. Для деяких класів інтегралів
(див.
нижче)
можна вказати відповідні підстановки.
Заміну змінної можна виконувати і у неявному виді, наприклад,
![]()
розуміючи
тут підстановку
![]() .
.
Л і т е р а т у р а: [4 ,гл. 6, § 1, п. 2; 5, гл. 5, § 5.2; 6, гл. Х, § 4].
