Формула Ньютона – Лейбница.

Пусть выполнены условия теоремы о полном дифференциале и пусть выражение

- полный дифференциал, а функция - потенциал.

Тогда справедлива формула Ньютона – Лейбница

, где - потенциал.

Доказательство. В теореме о полном дифференциале доказано, что потенциал можно записать в виде . Так как интеграл не зависит от пути интегрирования, то дугу, соединяющую точки (x₁, y₁), (x₂, y₂) можно провести через точку (x₀, y₀). Поэтому = + = - = .

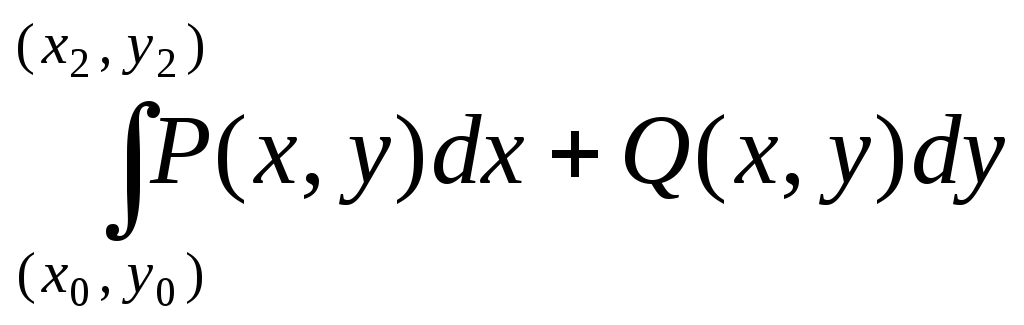Теорема (о полном дифференциале) для пространственной кривой.

Пусть дуга AB лежит на кусочно-гладкой поверхности S, пусть функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны и имеют непрерывные частные производные на S. Тогда следующие четыре утверждения эквивалентны.

1. не зависит от формы дуги (от пути интегрирования), а зависит только от начальной и конечной точек дуги.

2. Для любого замкнутого контура

3. 

4. . - полный дифференциал.

Доказательство. Доказательство аналогично двумерному случаю, схема доказательства та же: . Докажите ее самостоятельно.

проводится по теореме о смешанных производных так же как в двумерном случае.

проводится по теореме Стокса (будет сформулирована и доказана ниже).

доказательство полностью аналогично двумерному случаю.

доказательство аналогично двумерному случаю.

Замечание. Формула Ньютона-Лейбница справедлива в трехмерном случае и доказывается так же.

Вычисление криволинейного интеграла от полного дифференциала.

Криволинейный интеграл от полного дифференциала можно вычислять двумя способами.

1. Можно выбирать удобный путь интегрирования, например, состоящий из отрезков, параллельных OX и OY. На отрезке, параллельном OX, dy=0, так как y не изменяется на этом отрезке. На отрезке, параллельном OY, dx=0, так как x не изменяется на этом отрезке. Тогда = +

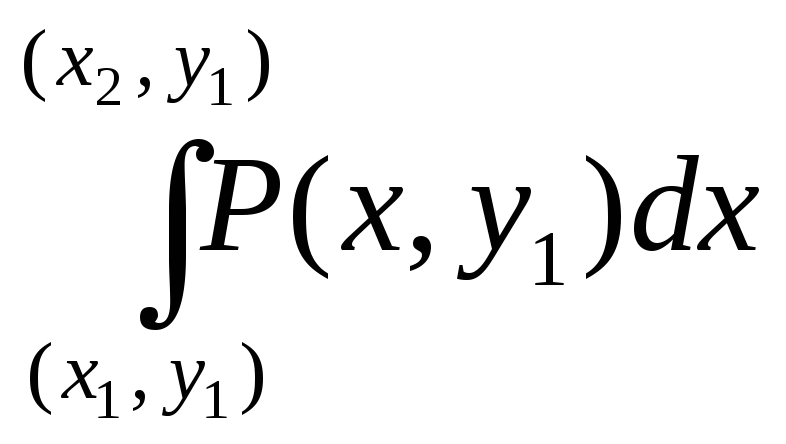2. Можно восстановить потенциал, как это делалось на первом курсе при решении дифференциальных уравнений в полных дифференциалах и применить формулу Ньютона-Лейбница.

Пример. Вычислить интеграл .

1. =

2. 

.

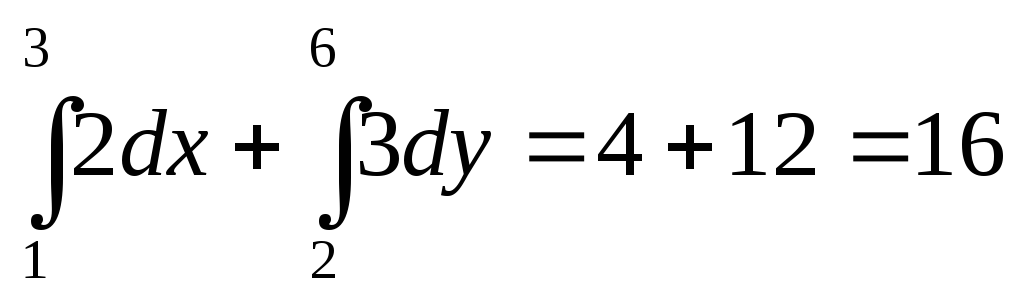
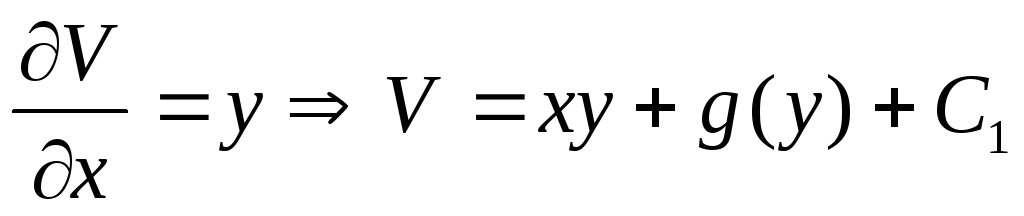
Сравнивая две записи потенциала, получим .

=.

Заметим, что аналогично вычисляется криволинейный интеграл от полного дифференциала по пространственной кривой.

Формула Грина для многосвязной области.

Пусть кусочно-гладкие контуры лежат внутри контура и вне друг друга. Пусть непрерывны и имеют непрерывные частные производные по переменным x, y в области между контурами и на самих этих контурах. Тогда

D m A K B E p q r s n

Соединим контуры линиями AB, CD, EK. По формуле Грина для односвязной области криволинейные интегралы по контуру AbpCDqEKmA и по контуру AnKEsDCrBA равны двойным интегралам для верхней Dверх и нижней Dнижн областей. Представим эти интегралы как сумму интегралов по составляющим контуры дугам и сложим эти интегралы, сокращая интегралы по одним и тем же дугам в разных направлениях

=

=

Складывая интегралы, получим

=.

Отсюда имеем

= . Теорема доказана для случая n = 2. Для n > 2 доказательство аналогично.

Следствие 1. Пусть Pdx+Qdy – полный дифференциал и n=1.

Тогда. Поэтому, если в какой-либо точке нарушается непрерывность функций, P, Q или их частных производных, то интеграл может быть взят по любому кусочно-гладкому не самопересекающемуся контуру, охватывающему эту точку (мы получим один и тот же результат).

Следствие 2. Пусть Pdx+Qdy – полный дифференциал Если кусочно-гладкий контур один раз охватывает некоторую точку, , а контур L n раз охватывает эту точку, то в условиях теоремы . Докажите это самостоятельно.