9. С помощью каких методов и на базе каких исходных данных решается задача выявления основных типов потребительского потребления.

Ответ:

Имеются данные о структуре и объемах потребительских расходов n-российских семей в виде выборки y₁, y₂, … , y_n.

Исходная информация для задачи:

1) бюджеты домашних хозяйств;

2) RLMS – данные бюджетов 4 тыс. семей за 199602000 гг.

Пусть имеется выборка из генеральной совокупности семей объемом n, законы распределения которой описываются смесью как нормальных законов, причем k-неизвестных с функцией плотности вида:

,

где известный вектор θ включает все неизвестные параметры модели: θ (k, π₁, … π_k-1, а₍₁₎, …, а_(к), ∑_{(1), … ,} ∑_(к)).

Требуется по выборке V_n получить наилучшие оценки вектора θ, а также предложить такое правило классификации , которая позволила бы классифицировать имеющиеся n-наблюдений по -типов потребительского поведения с наименьшей вероятностью ошибки классификации. При этом предполагается, что каждый тип потребительского поведения описывается многомерным нормальным распределением с параметрами (а_(j); ∑_(j)).

Эта задача известна в многомерном статистическом анализ как задачи классификации, основанные на смеси нормальных распределений.

11. Синтетические категории и интегральные индикаторы.

Ответ:

Синтетические категории:

• Качество жизни населения

• Уровень благосостояния

• Качество социальной сферы

• Экологическая ниша

• Природно-климатические условия

Интегральный индикатор Y:

Y = f ( x⁽¹⁾ , x⁽²⁾ , …., x^(p) )

Y⁽¹⁾ = f₁ (x⁽¹⁾ , x⁽²⁾ , …., x^(p) ) x ^(j) → x^~(j) – унифицированный показатель

Y ^(k) = f_k (x⁽¹⁾ , x⁽²⁾ , …., x^(p) )

- значение j-показателя, соответствующего наилучшему значению

1. связан с качеством жизни населения, монотонно возрастающая зависимость

- частный случай общей формулы

2. связан с качеством жизни населения, монотонно убывающая зависимость

-частный случай общей формулы

3. связан с немонотонно зависимостью

Примеры:

1. сравнительный межотраслевой, межрегиональный анализ социально-экономического развития

источник: WCY – ежегодник мировой конкурентоспособности ( 49 стран, 250 показателей)

2. оценка эффективности проведения социально-экономической политики

3. формирование социально-экономической политики, измерители уровня социальной напряженности в обществе – коэффициент фондов – 10% бедных / 10% богатых

4. социально-экономическое развитие, обладающее свойством с условием гарантированного поколения, Y – индикатор устойчивого развития страны по частным критериям, отражающий ситуацию в стране в будущем

, x^(j) –измеряется в одних и тех же шкалах

1. – условный и ограниченный в пространственных и временных рамках

2. – четкая прикладная направленность исследования, в рамках которой мы собираемся использовать индикаторы.

Источники: статистический ежегодник рф

12. Интегральный индикатор синтетической категории социально-экономического развития или качества жизни как свертка статистически регистрируемых социально-экономических показателей (частных критериев анализируемой синтетической категории). Какие статистически регулируемые социально-экономические показатели Вы включили бы в набор частных критериев при построении интегральных индикаторов (линейных сверток) для каждой из следующей синтетических категорий: качества населения; уровня благосостояния населения; качества социальной сферы; уровня образования населения; качества экологической ниши?

Ответ:

Один из эффективных и подходов к описанию и анализу поведения хозяйствующего субъекта (индивидуума, домашнего хозяйства, фирмы и т.д.) связан с построением соответствующей целевой функции, которая по существу является некоторой сверткой ряда частных поклей его поведения. Аналогичные задачи возникают при построении и анализе комплексных, агрегатных показателей какого-либо сложного свойства – качества населения, качества жизни, научно-производственного уровня производственной системы и т.п.

Качество жизни населения

Объект – субъекты, регионы РФ

Частные критерии – статистические показатели ():

• ожидаемая продолжительность жизни

• младенческая смертность

• характеристика естественного прироста

• характеристики смертности (от основных причин)

• % людей с высшим образованием в экономике

– скалярный ИИКЖ (интегральный индикатор качества жизни)

– мультикритериальная схема

- ?

Способы определения:

1. 

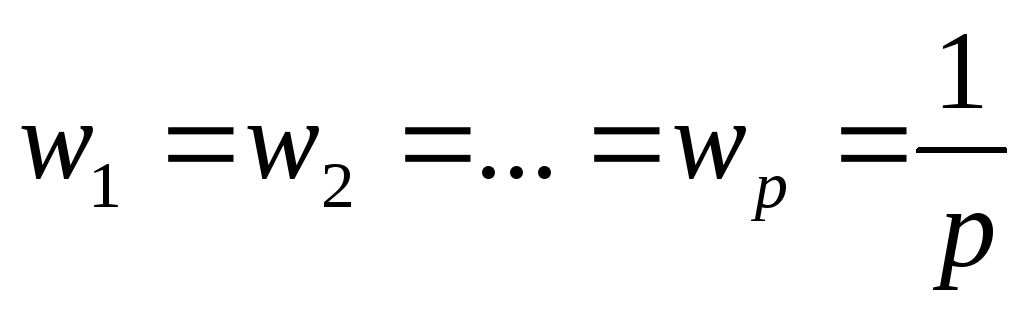
2. прямая экспертная оценка (вся ответственность на эксперте)

3. => оценка при наличие экспертного "обучения"

=> оценка без "обучения"

13. Описать основные формы так называемого "обучения" как части информационного обеспечения задачи построения интегральных индикаторов (ИИ) социально-экономического развития или качества жизни населения. Каковы методы построения ИИ в условиях наличия "обучения".

Ответ:

Формы "обучения":

1. Идеальный случай. Наиболее информативный – наиболее трудный для экспертов.

Оценка каждого веса (интегрального свойства) известна.

Регрессия y на

по МНК:

– регрессионные остатки

,

0. N

наихудш. качество наилучш. качество

2. Экспертная информация. Упорядоченные (по анализируемым синтетическим категориям) группы объектов.

Самая детальная информация – приписывание рангов каждому объекту.

i-ый объект => R_i=2

y:

0. – лидеры, если i-ый объект в 1 группе

1. – середняки, если i-ый объект во 2 группе

2. – аутсайдеры, если i-ый объект в 3 группе

Оценка параметров модели множественного выбора – анализ логит-моделей.

3. Парные сравнения объектов.

Самый простой способ. Не обязательно сравнивать все объекты.

могут быть заполнены не все элементы

;

l=1,2,…,k i_l, j_l =1,2,…,k

14. Почему 1-я главная компонента, построенная по набору частных критериев анализируемой синтетической категории, может быть хорошим решением в задаче построения интегрального индикатора этой синтетической категории в условиях отсутствия "обучения"? Описать процедуру построения 1-й главной компоненты по исходным статистическим данным.

Ответ:

z

b минимизируют ошибки прогнозов (подобраны по принципу НК)

пусть - 1ая главная компонента

1ая главная компонента – интегральный индикатор качества жизни

Унифицированные исходные данные:

1 свойство 1ой совокупности – по первому признаку можно сказать о всех.

Центрированная матрица Х:

упорядочено по величине собственных значений

p – количество собственных значений

1ая главная компонента:

Так как нас волнует только , то можно перейти к унифицированным компонентам

Чтобы интегральный показатель мерился по той же шкале.

Эту задачу нельзя решить с помощью 1го скалярного показателя, т.к. информативность 1ой главной компоненты измеряется долей дисперсии, которую она измеряет в общей доле дисперсии.

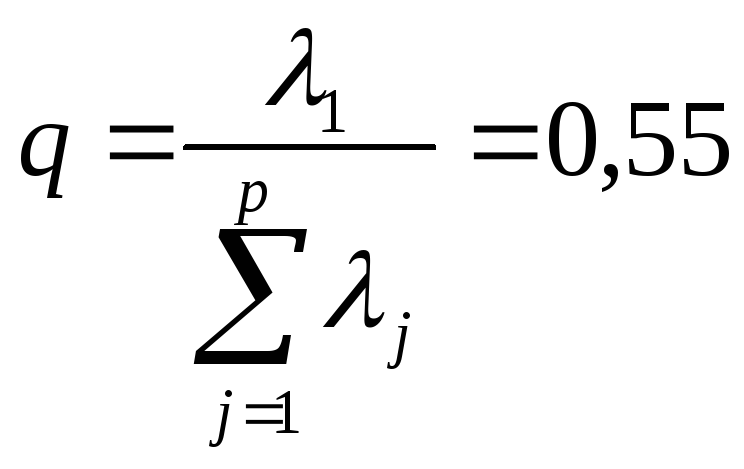, т.е. если , то не надо переходить к другим, т.е. то, что построили – верно.

При следует строить больше 1 индикатора качества жизни.