13. Системы линейных уравнений. Критерий совместности

Общий вид системы линейных уравнений:

(1)

()- решение системы –упорядоченная совокупность чисел, которые при подставлении в сумму вместо обращает уравнения системы (1) в верное равенство.

Запишем матрицу системы (1), добавив справа столбец свободных членов:

(2)

Матрица (2) расширенная матрица системы линейных уравнений.

Определение: Если в системе все b_к (k=1,...m) равны нулю, то такая система называется однородной. Если хотя бы один из них b_к0, то система называется неоднородной.

Определение: Система называется совместной, если она имеет хотя бы одно решение, в противном случае она называется несовместной.

Определение: Совместная система линейных уравнений называется определённой, если она имеет единственное решение и неопределённой - если решений множество.

Критерий совместности (Теорема Кронекера-Капелли): для того, чтобы система уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы и ранг расширенной матрицы были равны. ( или противоречива: ).

Доказательство: Необходимость. Пусть сумма (1)-совместна, докажем что , т.е. есть решения () и . Из последнего столбца м. вычтем линейную комбинацию столбцов матрицы A, получим матрицу

.

Достаточность. Пусть , докажем, что сумма совместна. Т.к. , то существует минор , который является базисным. На основании теоремы о базисном миноре последний столбец матрицы является линейной комбинацией остальных столбцов матрицы.

()- решение системы (1), т.е. система (1)-совместна.

14. Системы линейных уравнений. Критерий определенности.

Критерий определённости. Совместная система является определенной, если и неопределенной, если .( n – кол-во неизвестных.)

Доказательство а) Пусть - это значит, что столбцы матрицы A линейно зависимы, т.е. существуют числа не все равные нулю и такие, что (*). По условию система 1 совместна, т.е. существуют решения () системы (1)

(**). (*)+(**)=,т.е. - решение системы (1).

б)Пусть r =n (значит ), докажем, что сумма (1) – определена.

Пусть решений два, тогда ,,хотя бы одно , тогда ,но так как ранг матрицы А равен n ,то все столбцы матрицы А линейно независимы, значит линейная комбинация этих столбцов = 0, только когда все коэффициенты = 0, т.е. , …- противоречие => 1 решение.(ч.т.д.)

Замечание: Неопределённая сумма имеет б.много решений, т.к. из (*) и (**)следует, что , где k=0,1,-1,2,-2,… -является решениями.

15. Решение совместной определенной системы линейных уравнений.

А)Формула Крамера. а) Пусть m=n и |A|≠ 0, значит , т.е. система совместна и определенна.

(1) ← алгебраические дополнения элем. k-того столбца. Предположим что х₁…х_n не неизвестные а их значения. Т.е. все эти равенства верные. Сложим все строки системы:

A_k получается из матрица A заменой k-того столбца столбцом свободных членов, чужим столбцом. Отсюда получаем: - формулы Крамера.

16. Решение совместной неопределенной системы линейных уравнений.

В) Пусть имеется СЛУ с n неизвестными, причем . Для определенности будем считать что базисный минор матрицы А расположен в левом верхнем углу матрицы А. Этот же минор будет базисным и для расширенной матрицы системы. Каждая строка расширенной матрицы системы не пересекающая базисный минор является линейной комбинацией строк, пересекающих базисный минор поэтому система СЛУ (1) эквивалентна системе:

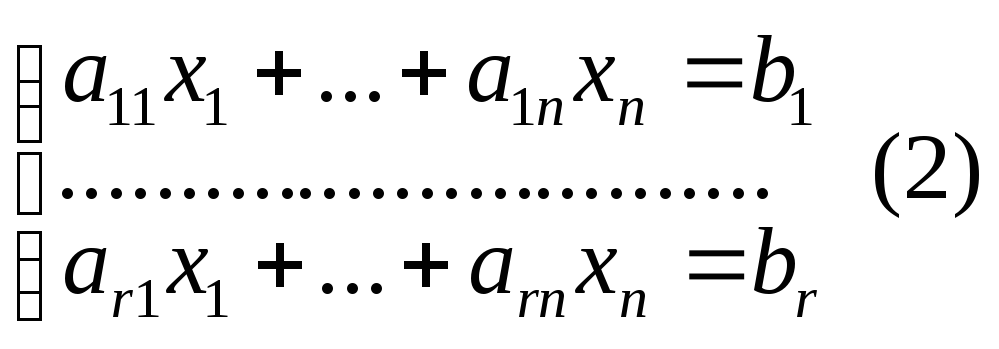. Если то неизвестные x_r+1…x_n называются свободными и слагаемые содержащие свободные неизвестные перенесем в правые части уравнений. Тогда система (2) примет вид: .

Неизвестные x₁…x_r - главные (базисные) неизвестные. Придавая свободным неизвестным различные значения из системы (3) мы будем каждый раз получать систему r уравнений с r неизвестными имеющие единственные решения . Т.к. определитель этой системы (3) есть базисный минор М≠0 объединяя (4) и (5) мы получаем общее решение системы (1): . Придавая величинам всевозможные значения из поля Р мы получаем все решения системы (1), каждое из которых называется частным в отличие от общего.

СЛУ можно решать матричным методом: АХ=В. Можно методом Гаусса: его суть в последовательном исключение неизвестных. Или методом Гаусса-Жордано: Представляет собой модификацию метода Гаусса, вместо того чтобы исключить x_k только в уравнениях k+1…n исключают x_k также и в уравнениях 1…k-1. При решении системы методом Гаусса-Жордано выбирают разрешающее уравнение и разрешающее неизвестное. В качестве разрешающего уравнения можно взять любое уравнение системы. А в качестве разрешающей неизвестной, неизвестное, коэффициенты при котором в выбранном уравнении отличны от 0. Далее делим обе части разрешающего уравнения на коэффициенты при разрешающем неизвестном и исключаем разрешающее неизвестное из всех уравнений системы кроме разрешающего. Преобразования производим до тех пор пока каждое уравнение системы не побывает в качестве разрешающего.