- •1. .Понятие числового поля и матрицы над полем р. Доказать, что любая транспозиция меняет характер четности перестановки. Определение Определителя n-ого порядка.
- •2. Свойства определителя матрицы
- •2) Теорема о перестановке 2х строк матрицы оределителя. Определитель с двумя одинаковыми строками.
- •3) Теорема об умножении некоторой строки матрицы определителя на одно и то же число. Определитель с двумя пропорциональными строками.
- •4). Теорема о разложении определителя на сумму определителей и следствия из нее.
- •3. Операции над матрицами и их свойства. Доказать одно из них.
- •4 Определение обратной матрицы. Доказать что у каждой обратимой матрицы существует лишь одно обращение.
- •7. Блочные матрицы. Сложение и умножение блочных матриц. Теорема об определителе квазитреугольной матрицы.
- •8. Теорема об определителе произведения матриц.
- •9 Теорема о существовании обратной матрицы.
- •10.Определение ранга матрицы. Теорема о базисном миноре и следствие из неё.
- •11 Понятие о линейной зависимости строк и столбцов матрицы. Теорема о ранге матрицы.
- •12. Методы вычисления ранга матрицы: метод окаймляющих миноров, метод элементарных преобразований.
- •13. Системы линейных уравнений. Критерий совместности
- •14. Системы линейных уравнений. Критерий определенности.
- •15. Решение совместной определенной системы линейных уравнений.
- •16. Решение совместной неопределенной системы линейных уравнений.
- •17. Необходимое и достаточное условие чтобы ослу имела ненулевое решение
- •18. Теорема о существовании фундаментальной системы решений.
- •19. Теорема о связи между решениями неоднородных и соответствующих однородных систем
- •20. Линейные операции над векторами и их свойства.
- •21 Определение разности двух векторов. Доказать что для любых векторов и разность существует и единственна.
- •22. Определение базиса, координаты вектора в базисе. Теорема о разложении вектора по базису.
- •23. Линейная зависимость векторов. Свойства понятия линейной зависимости, доказать одно из них.
- •24 Декартовы системы координат в пространстве, на плоскости и на прямой. Теорема о линейной комбинации векторов и следствия из нее.
- •25. Вывод формул выражающих координаты точки в одной дск через координаты этой же точки в другой дск.
- •26 Скалярное произведение векторов. Определение и основные свойства.
- •27. Векторное произведение векторов. Определение и основные свойства.
- •28. Смешанное произведение векторов. Определение и основные свойства.
- •29. Смешанное произведение через координаты
- •33. Двойное векторное произведение векторов. Определение и формула для вычисления( без доказательства).
- •32. Общие уравнения плоскости и прямой.
- •33. Переход от общих уравнений плоскости и прямой на плоскости к их параметрическим уравнениям. Геометрический смысл коэффициентов а,в,с (а,в) в общем уравнении плоскости(прямой на плоскости).
- •34. Исключение параметра из параметрических уравнений на плоскости( в пространстве), канонические уравнения прямой.
- •35. Векторные уравнения прямой и плоскости.
- •36. Общие уравнения прямой в пространстве, приведение к каноническому виду.
- •37, Уравнение прямой через две точки. Уравнение прямой проходящей через три точки. Признак параллельности прямой и плоскости.
- •38.Полупространство, полуплоскость. Расстояние от точки до плоскости
- •39. Нормальным уравнением плоскости. Отклонение???
- •40. Расстояние между параллельными прямыми
- •42.Определение эллипса. Каноническое уравнение эллипса. Параметрические уравнения эллипса.
- •43. Определение гиперболы. Каноническое уравнение гиперболы. Асимптоты гиперболы..
- •44. Определение параболы. Вывод канонического уравнения параболы.
- •45. Эксцентриситет эллипса и гиперболы. Директрисы теорема
- •46. Эксцентрисетет параболы и т.Д
- •47. Кривые второго порядка и их классификация. Основная теорема о квп.
- •48. Поверхности второго порядка и их классификация. Основная теорема о пвп. Поверхности вращения.
- •49. Основная теорема о пвп. Поверхности вращения
24 Декартовы системы координат в пространстве, на плоскости и на прямой. Теорема о линейной комбинации векторов и следствия из нее.
Ф иксируем
в пространстве любую точку О - начало
системы координат. Пусть
иксируем
в пространстве любую точку О - начало
системы координат. Пусть
![]() -
базис в пространстве, отложим векторы
-
базис в пространстве, отложим векторы
![]() от точки О. Три плоскости определяемые
попарно координатными осями называются
координатными плоскостями. Будем
говорить, что мы построили систему
координат. Пусть
от точки О. Три плоскости определяемые
попарно координатными осями называются
координатными плоскостями. Будем
говорить, что мы построили систему
координат. Пусть
![]() - произвольный вектор, его можно
единственным образом представить в
виде
- произвольный вектор, его можно
единственным образом представить в
виде
![]() . Коэффициенты x,y,z
в называются координатами вектора
. Коэффициенты x,y,z
в называются координатами вектора
![]() в пространстве. Они независят от выбора
начала координат.
в пространстве. Они независят от выбора
начала координат.
![]() -
проекции вектора
-
проекции вектора
![]() на координатные оси Ox,
Oy,Oz,
а числа x,y,z
– являются величинами этих проекций
соответственно, если
на координатные оси Ox,
Oy,Oz,
а числа x,y,z
– являются величинами этих проекций
соответственно, если
![]() -
масштабные векторы соответствующих
координатных осей. Если система координат
задана то для указания вектора употребляют
запись
-
масштабные векторы соответствующих
координатных осей. Если система координат
задана то для указания вектора употребляют
запись
![]() (x,y,z).
Пусть М – произвольная точка пространства.
(x,y,z).
Пусть М – произвольная точка пространства.
![]() - радиус вектор этой точки. Декартовыми
координатами точки М называются
координаты (x,y,z)
ее радиус вектора(смотри рисунок).
Координаты точки зависят от начала
выбора системы координат.
- радиус вектор этой точки. Декартовыми
координатами точки М называются
координаты (x,y,z)
ее радиус вектора(смотри рисунок).
Координаты точки зависят от начала
выбора системы координат.
Простейшая
Декартова система координат –
прямоугольная. В случае ПДСК векторы
![]() - попарно ортогональны и длина каждого
из них, измеренная масштабной единицей
принятой для всего пространства равна
1. В ПДСК базисные векторы обозначаются
- попарно ортогональны и длина каждого
из них, измеренная масштабной единицей
принятой для всего пространства равна
1. В ПДСК базисные векторы обозначаются
![]() (ось
ОХ),
(ось
ОХ),
![]() (ось ОY),
(ось ОY),
![]() (ось
ОZ).
Все проекции в этом случае предполагаются
прямоугольными. В отличие от
специальных(ПДСК) ДСК в общем случае
называются общими ДСК.
(ось
ОZ).
Все проекции в этом случае предполагаются
прямоугольными. В отличие от
специальных(ПДСК) ДСК в общем случае
называются общими ДСК.
Б азисная
тройка векторов подразделяется на два
типа правая и левая. Базис
азисная
тройка векторов подразделяется на два
типа правая и левая. Базис
![]() называется
называется
правым, если при наблюдении с
конца третьего вектора кратчайший поворот от первого вектора ко второму осуществляется против часовой стрелки и наоборот. Соответствующие им системы координат также называются правыми и левыми.
Замечание: Если длины базисных векторов равны 1 то СК называется нормированной. Во многих случаях длина вектора называется его нормой. Если базисные вектора попарно ортогональны то и СК – ортогональная. Ортогональная и нормированная СК называется ортонормированной.
Координаты линейной комбинации векторов. Введение координат для векторов позволяет сводить различные соотношения между векторами к числовым соотношениям между их координатами.
Теорема: Координаты линейных комбинаций векторов равны таким же линейным комбинациям соответствующих координат линейных векторов.
Доказательство: Координаты векторов есть величины их проекций на соответствующих координатных осях. Но тогда утверждение теоремы следует из теоремы о величинах проекций линейных комбинаций векторов.
![]() это
равносильно следующей системе равенств
это
равносильно следующей системе равенств

С ледствие
1:
ледствие
1:
![]()
![]()
Следствие 2: Для того чтобы два вектора были коллинеарны необходимо и достаточно чтобы их координаты были пропорциональны.
Доказательство:
Пусть
вектор
![]() параллелен вектору
параллелен вектору
![]() следовательно
следовательно
![]()
![]()
![]() .
Векторное равенство (**) равносильно:
.
Векторное равенство (**) равносильно:
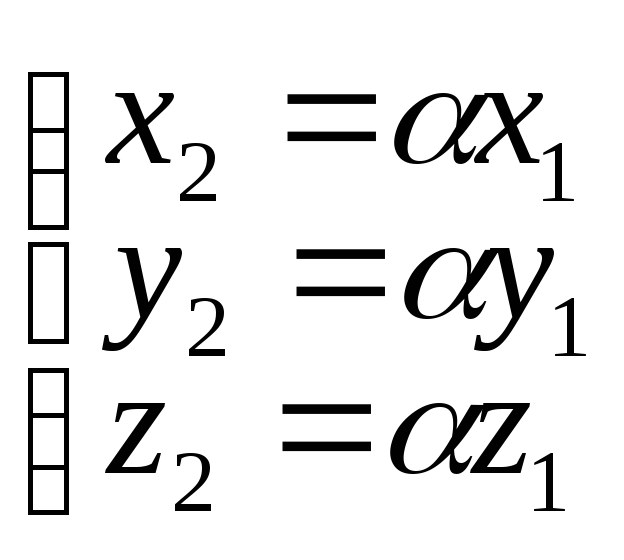 Если все координаты отличны от 0 то
Если все координаты отличны от 0 то
![]() .
.
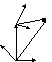
25. Вывод формул выражающих координаты точки в одной дск через координаты этой же точки в другой дск.
![]()
![]()
В
старой системе:
![]()
![]()
![]() .
.
![]()
![]()
В
силу единственности разложения вектора
по базису получим:
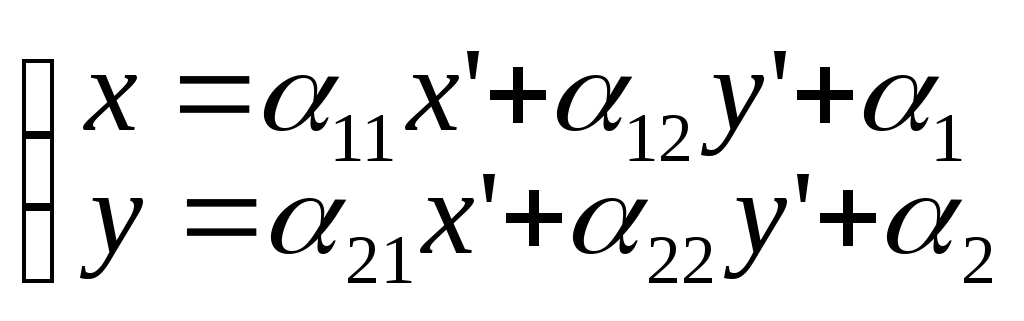 .
Эти формулы выражают старые координаты
точки М через ее новые координаты.
.
Эти формулы выражают старые координаты
точки М через ее новые координаты.
![]()
![]()
![]()
![]()
![]() тогда
связь между новыми и старыми координатами:
тогда
связь между новыми и старыми координатами: