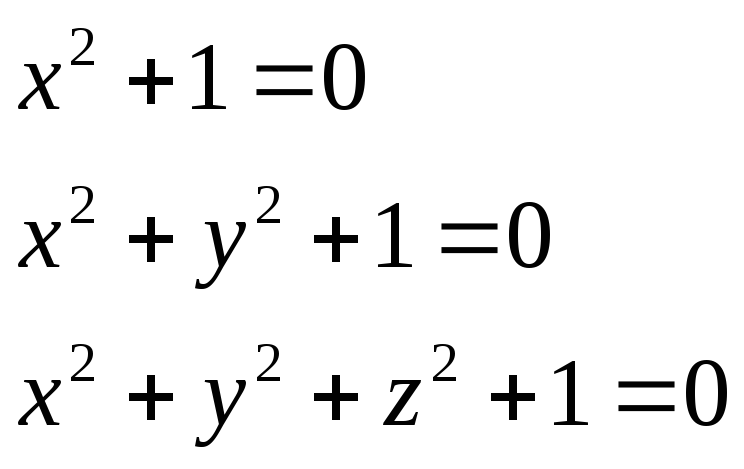44. Определение параболы. Вывод канонического уравнения параболы.

Определение: Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а фиксированная прямая – директрисой параболы.

Для вывода уравнения построим:

Согласно определению:

Так как у²>=0 то парабола лежит в правой полуплоскости. При х возрастающем от 0 до бесконечности . Парабола симметрична относительно Ох. Точка пересечения параболы со своей осью симметрии называется вершиной параболы.

45. Эксцентриситет эллипса и гиперболы. Директрисы теорема

Определение. Эксцентриситет эллипса – отношение половины расстояния между фокусами к длине его большей оси: .

Так как , следовательно < 1. , следовательно,

Замечание: Эксцентриситет эллипса можно рассматривать как меру его вытянутости. Чем больше эксцентриситет тем меньше отношение (малой оси эллипса к его большой полуоси).

Эксцентриситет гиперболы. Пусть с- половина расстояния между фокусами гиперболы, а – действительная полуось гиперболы.

Определение: Эксцентриситетом гиперболы называется величина .

Учитывая связь между c,a,b получим: . Эксцентриситет гиперболы больше 1.

Замечание: Эксцентриситет гиперболы можно рассматривать как величину раствора угла между его асимптотами, т.к. , где φ – величина угла между асимптотами гиперболы.

46. Эксцентрисетет параболы и т.Д

47. Кривые второго порядка и их классификация. Основная теорема о квп.

Существует 8 типов КВП:

1.эллипсы

2.гиперболы

3.параболы

Кривые 1,2,3 – канонические сечения. Если пересечь конус плоскостью параллельной оси конуса то получим гиперболу. Если плоскостью параллельной образующей то параболу. Все плоскости не проходят через вершину конуса. Если любой другой плоскостью то эллипс.

4.пара параллельных прямых y²+ a²=0, a0

5.пара пересекающихся прямых y²- k² x²=0

6.одна прямая y²=0

7.одна точка x²+ y²=0

8.пустое множество - пустая кривая (кр. без точек) x²+ y²+1=0 или x²+ 1=0

Теорема(основная теорема о КВП): Уравнение вида

a₁₁ x² + 2 a₁₂ x y + a₂₂ y² + 2 a₁ x + 2 a₂ y + a₀ = 0

может представлять только кривую одного из указанных восьми типов.

Идея доказательства состоит в том чтобы прейти к такой системе координат в которой уравнение КВП примет наиболее простой вид, когда тип кривой, которую оно представляет становится очевидным. Теорема доказывается с помощью поворота системы координат на такой угол при котором член с произведением координат исчезает. И с помощью параллельного переноса системы координат при котором исчезает или член с переменной х или член с переменной у.

Переход к новой системе координат: 1. Параллельный перенос

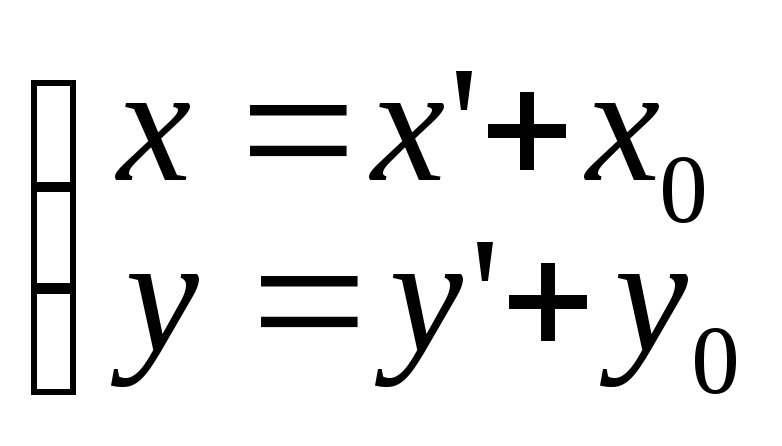
2. Поворот

48. Поверхности второго порядка и их классификация. Основная теорема о пвп. Поверхности вращения.

ПВП - множество точек прямоугольные координаты которых удовлетворяют уравнению 2 степени: (1)

Предполагается, что хотя бы один из коэффициентов при квадратах или при произведениях отличен от 0. Уравнение инвариантно относительно выбора системы координат.

Теорема Любая плоскость пересекает ПВП по КВП за исключением особого случая, когда в сечении – вся плоскость.(ПВП может быть плоскостью или парой плоскостей).

Существует 15 типов ПВП. Перечислим их указав уравнения, которыми они задаются в подходящих системах координат. Эти уравнения называются каноническими(простейшими). Строят геометрические образы соответствующие каноническим уравнениям методом параллельных сечений: Пересекают поверхность координатными плоскостями и плоскостями параллельными им. В результате получают сечения и кривые, которые дают представление о форме поверхности.

1. Эллипсоид.

Если a=b=c то получаем сферу.

2. Гиперболоиды.

1). Однополостный гиперболоид:

Cечение однополостного гиперболоида координатными плоскостями: XOZ: - гипербола.

YOZ: - гипербола.

Плоскостью XOY: - эллипс.

2). Двуполостной гиперболоид.

Начало координат – точка симметрии.

Координатные плоскости – плоскости симметрии.

Плоскость z = h пересекает гиперболоид по эллипсу , т.е. плоскость z = h начинает пересекать гиперболоид при | h |  c. Сечение гиперболоида плоскостями x = 0 и y = 0 - это гиперболы.

Числа a,b,c в уравнениях (2),(3),(4) называются полуосями эллипсоидов и гиперболоидов.

3. Параболоиды.

1). Эллиптический параболоид:

Сечение плоскостью z = h есть , где . Из уравнения видно, что z  0 – это бесконечная чаша.

Пересечение плоскостями y = h и x=h - это парабола и вообще

2). Гиперболический параболоид:

Очевидно, плоскости XOZ и YOZ – плоскости симметрии, ось z – ось параболоида. Пересечение параболоида с плоскостью z = h – гиперболы: , . Плоскость z=0 пересекает гиперболический параболоид по двум осям которые являются ассимптотами.

4. Конус и цилиндры второго порядка.

1). Конус – это поверхность . Конус образован прямыми линиями, проходящими через начало координат 0 ( 0, 0, 0 ). Сечение конуса – это эллипсы с полуосями .

2). Цилиндры второго порядка.

Это эллиптический цилиндр .

Какую бы прямую мы не взяли пересекающую эллипсы и параллельную оси Oz то она удовлетворяет этому уравнению. Перемещая эту прямую вокруг эллипса получим поверхность.

Гиперболический цилиндр:

На плоскости ХОУ это гипербола. Перемещаем прямую пересекающую гиперболу параллельно Oz вдоль гиперболы.

Параболический цилиндр: На плоскости ХОУ это парабола. Цилиндрические поверхности образуются прямой(образующей) перемещающейся параллельно самой себе вдоль некоторой прямой(направляющей).

Далее идут ПВП состоящие из плоскостей.(это тоже цилиндры т.к. плоскость состоит из параллельных прямых).

10. Пара пересекающихся плоскостей

11.Пара параллельных плоскостей

12. - прямой

13.Прямая – «цилиндр», построенный на одной точке

14.Одна точка

15.Пустое множество