35. Множество истинности предикатов. Равносильность и следование предикатов.

Одноместным предикатом Р(x) называется произвольная функция переменного x, определенная на множестве M и принимающая значение из множества {1; 0}. Множество М, на котором определен предикат Р(x), называется областью определения предиката Р(x). Множество всех элементов , при которых предикат принимает значения “истина”, называется множеством истинности предиката Р(x),Опред 1.

Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М. Опред 2. Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области

Пусть А(х) и В(х) – переменные предикаты, Тогда имеют место равносильности:

. .

.

Множество предложений G влечёт предложение F, или формула F является логическим следствием G (символически, G |= F), если для каждой интерпретации, при которой истинны все предложения из G, F также истинно.

36. Семантика языка логики предикатов, интерпретация формул. Три ситуации при логической интерпретации формул логики предикатов. Проблемы получения истинных формул и проверки формулы на истинность. Эквивалентные соотношения логики предикатов.

Предикат (сказанное) – высказывательная функция, определенная на некотором множестве М, т.е. такая n-местная функция Р, которая каждому упорядоченному набору (х1, К, хn) элементов множества М, сопоставляет некaоторое высказывание, обозначенное Р(х1, K, хn). Р называется n-местным предикатом на М. Под 0 – местным предикатом понимается произвольное высказывание. M — предметная область предиката,x1, …,xn — предметные переменные.

Предикат x₁>x₂ является двухместным предикатом, предметной областью которого могут служить любые множества действительных чисел. Высказывание 6>5 истинно, а высказывание 3>10 ложно. Если вместо одной из переменных подставить число, то получится одноместный предикат: x₁>3,5>x₂ и так далее.

Основные ситуации.

1. Если в области M для формулы F существует такая подстановка констант вместо всех переменных, что F становится истинным высказыванием, то эта формула называется выполнимой в области M. Если существует область M, в которой формула F выполнима, то формула называется просто выполнимой. Пример выполнимой формулы - .

2. Если формула F выполнима в области M при любых подстановках констант, то она называется тождественно истинной в области M. Формула, тождественно истинная в любых множествах называется просто тождественно истинной, или общезначимой, или тавтологией. Например, формула тождественна для всех множеств, состоящих из одного элемента, а формула 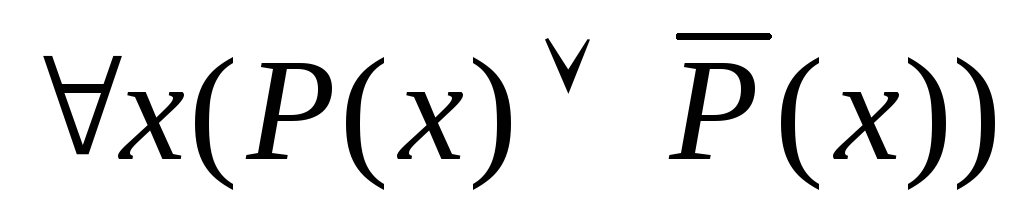является тавтологией.

3. Если формула F невыполнима в области M при любых подстановках констант, то она называется тождественно ложной в области M. Формула, тождественно ложная в любых множествах называется просто тождественно ложной или противоречивой. Формула 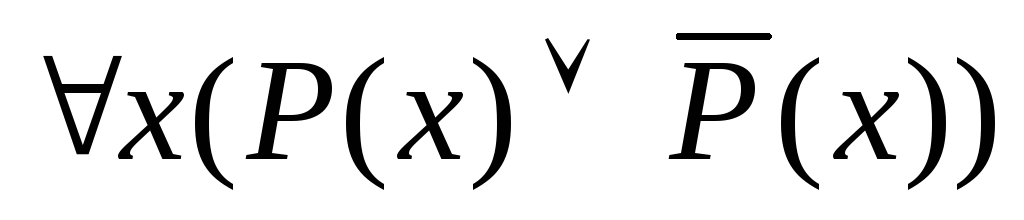является противоречивой.

Моделью M в логике предикатов называется множество М вместе с заданной на нем совокупностью предикатов S={P1, …, Pk} :

M = (М; P1, …, Pk), где М — основное множество модели M ; S={P1, …, Pk} — сигнатура модели M .

Формулы называются эквивалентными, если при любых подстановках констант они принимают одинаковые значения.

В частности, все тождественно истинные формулы (и все ложные формулы) эквивалентны.

Вписать эквивалентные соотношения