45. Дифференциальные уравнения, допускающие понижение порядка

Укажем некоторые виды дифференциальные уравнений, допускающих понижение порядка.

I. Уравнение вида . После n-кратного интегрирования получается общее решение

II. Уравнение не содержит искомой функции и её производных до порядка  включительно:

Порядок такого уравнения можно понизить на  единиц заменой . Тогда уравнение примет вид

Из последнего уравнения, если это возможно, определяем , а затем находим  из уравнения  k-кратным интегрированием.

III. Уравнение не содержит независимого переменного:

Подстановка  позволяет понизить порядок уравнения на единицу. При этом  рассматривается как новая неизвестная функция от . Все производные  выражаются через производные от новой неизвестной функции  по 

Подставив эти выражения вместо  в уравнение, получим дифференциальное уравнение (n–1)-го порядка.

IV. Уравнение , однородное относительно аргументов , т.е.

Порядок такого уравнения может быть понижен на единицу подстановкой , где  — новая неизвестная функция от .

V. Уравнение, записанное в дифференциалах,

в котором функция  однородна относительно своих аргументов , если считать  и  — первого измерения, а  и т.д. — измерения . Тогда  будет иметь измерение ,  – измерение  и т.д.

Для понижения порядка применятся подстановка . В результате получается дифференциальное уравнение между  и , не содержащее явно , т. е допускающее понижение порядка не единицу (случай III).

Рассмотрим примеры на различные случаи понижения порядка дифференциального уравнения.

46. . Интегрирование ЛОДУ второго порядка с постоянными коэффициентами

Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами.

Пусть дано ЛОДУ второго порядка

где р и q постоянны.

Для нахождения общего решения уравнения (4.1) достаточно найти два его частных решения, образующих фундаментальную систему (см. теорему 3.5).

Будем искать частные решения уравнения (4.1) в виде

где k - некоторое число (предложено Л. Эйлером). Дифференцируя эту функцию два раза и подставляя выражения для у, у' и у" в уравнение (4.1), получим:

Уравнение (4.2) называется характеристическим уравнением ДУ (4.1) (для его составления достаточно в уравнении (4.1) заменить у", у' и у соответственно на k², k и 1).

При решении характеристического уравнения (4.2) возможны следующие три случая.

Случай 1. Корни k₁ и k₂ уравнения (4.2) действительные и различные:

В этом случае частными решениями уравнения (4.1) являются функции y₁=e^k1x и у₂=е_k2x. Они образуют фундаментальную систему решений (линейно независимы), т. к. их вронскиан

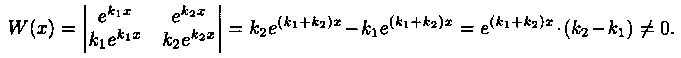
Следовательно, общее решение уравнения (4.1), согласно формуле (3.16), имеет вид

Пример 4.1. Ре