
- •1.Задачи физической защиты информации
- •2.Физические поля как носители информации.
- •4.Закон полного тока в интегральной форме.
- •3.Эл. Магнитное поле.
- •5.Закон индукции Фарадея в интегральной форме.
- •6.Закон Гаусса в интегральной форме.
- •7.Закон непрерывности магнитной индукции в интегральной форме.
- •8.Силовые характеристики эл. Магнитного поля
- •9.Количественные характеристики эл. Магнитного поля.
- •12. Ротор векторного поля.
- •13. Закон полного тока в дифференциальной форме.
- •15. Закон Гаусса в дифференциальной форме.
- •19. Граничные условия для нормальной составляющей вектора смещения вблизи границы раздела сред.
- •20. Теорема единственности теории эл. Магнитного поля.
- •21. Скалярный и векторный потенциалы электромагнитного поля и условия калибровки Лоренса.
- •23. Запаздывающие потенциалы электромагнитного поля.
- •25. Поле ближней зоны и поля индукции электрического диполя.
- •26. Поле дальней зоны электрического диполя.
- •27. Поле плоской волны в однородной среде.
- •29. Коэффициент фазы. Коэффициент затухания плоской волны.
- •32. Классификация физических сред по электромагнитным свойствам.
- •33. Материальные уравнения электромагнитного поля.
- •34. Тензоры электрической, магнитной проницаемости, проводимости.
- •35. Система уравнений Максвелла электромагнитного поля.
- •36. Коэффициент Френеля.
- •37. Распространение волн в продольно неоднородной среде.
- •38. Рекуррентная процедура расчета полей в продольно неоднородной среде.
- •40. Закон полного прохождения плоской волны через границу раздела двух сред.
- •56. Уравнение Максвелла в комплексной формуле для sin-идальных полей.
- •53.51.50.48. Экранирование электрического поля с помощью производящего экрана
- •43,44 Волны в поперечно неоднородных средах
- •45,46,47 Эл маг поле в проводнике(релаксация)
- •59,60 Преобразования Фурье
- •54.55 Коэффициенты Френеля
45,46,47 Эл маг поле в проводнике(релаксация)
э/м
поле-совокупность магн и эл полей,
которые при определенных условиях
могут друг друга порождать. э/м поля в
проводниках рассматривается как э/м
поля в среде, где много свободных
электронов , описывается так же с помощью
уравнений максвелла . в проводнике
имеются эл заряды свободно перемещающиеся
под действием эл сил ! поэтому если
возникло в проводнике эл. Поле то
свободные заряж. частицы проводника
придут в движение под действием этого
поля т е через проводник будет идти
ток. Но зяряды после некоторых перемещений
приходят в состояние равновесия т е
заряды распределяются по проводнику
та , что поле создаваемое ими внутри
проводника компенсирует внешнее поле
вызвавшее перемещение зарядов Е=0 и Н=0




В проводнике отсутствуют объемные заряды в равновесном состоянии
Релаксация зарядов в проводнике –это падение эл напряжения (разность эл потенциалов)
Длина релаксации состоит в том что на участках проводника такой длины падение эл. Напряжение равно отношению плотности эл нергии к плотности носителей заряда
Время релаксации эл зарядов-плотность зарядов падает в е раз :


За счет релаксации эл. Зарядов поле Е в проводнике чаще всего равно 0.
59,60 Преобразования Фурье
Система, поперечное сечение которой представляет собой кусочно однородные области из магнитно-диэлектрического материала с малыми потерями или металла с высокой проводимостью ,которая образует электроды направляющей системы вдоль координаты параллельной направлению системы ! эти свойства вытекают из уравнения максвелла

Е(r, )-
спектр реального поля , комплексная
векторная функция пространственных
координат.находится с помощью прямого
преобразования фурье
)-
спектр реального поля , комплексная
векторная функция пространственных
координат.находится с помощью прямого
преобразования фурье
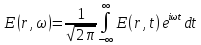

С точки зрения изучения свойств направляющей системы надо рассмотреть прохождения направляющей системы каждой спектральной составляющей поля.








54.55 Коэффициенты Френеля
Рассмотрим отражение и преломление плоской волны поляризованной перпендикулярно плоскости падения:
Eot+Eos=En- 1
Rt=
1
Rt=
T1=
Параллельно:
Rt=
Tt=
